圓錐曲線有很多奇妙的性質。下面我們來探讨一下雙曲線的一個性質及其應用。
性質:A是雙曲線
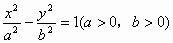
上的一點,l1,l2是它的兩條漸近線,作

交l1于B,

交

于C,則|AB|·|AC|為定值。
證明:因sin∠BOC為定值,

,故隻需證得|AD|·|AE|為定值。設點A(x0,y0),而

的方程為

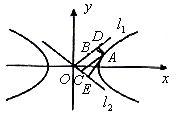
點A到的距離|AD|為

同理,點A到的距離|AE|為
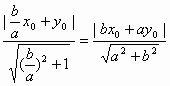
因此,

又

,即

因此,

為定值,即|AB|·|AC|為定值。
我們完成了這個性質的證明,但我們并未得到這個定值。由于這個性質的存在,我們可以用取特殊點的方法或通過計算sin∠BOC而得到定值。計算可得定值為
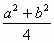
,請讀者自己證明。
這是雙曲線一個很有用的性質,熟練應用可以把一些問題化繁為簡。請看下面兩例。
例1. 如下圖,已知雙曲線
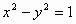
,一條直線分别與雙曲線及雙曲線的漸近線交于A、B、C、D四點,且

,k為常數,求ΔAOD的面積。
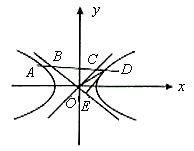
解:作DE⊥BO,垂足為E
∵題中雙曲線的兩條漸近線互相垂直
∴CO//DE。由性質可知

則

故
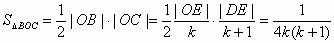
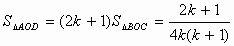
例2. 如下圖,已知兩點A、C在雙曲線C1:

上,B、D在另一與C1共漸近線的雙曲線C2上,四邊形ABCD為平行四邊形,且鄰邊分别平行兩條漸近線,求C2的方程。

初看這道題,或許有點找不着思路,因為按照常規計算,計算量是很大的。如果利用雙曲線的上述性質,問題會迎刃而解。
解:設AB交漸近線

于
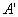
,CD交漸近線于

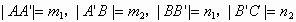
由性質可知:

又
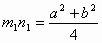
,所以

設
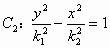
,則
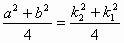
由于兩雙曲線共漸近線,則

所以,

,故

▍ 來源:綜合網絡
▍ 編輯:Wordwuli
▍ 聲明:如有侵權,請聯系删除;若需轉載,請注明出處。
,更多精彩资讯请关注tft每日頭條,我们将持续为您更新最新资讯!




