高中數學必修2平行關系判斷-tft每日頭條

高中數學必修2平行關系判斷

教育更新时间:2024-05-09 20:58:10

今天分析空間内直線與平面之間内的位置關系。

一、直線與直線的位置關系：

共面直線：即在同一平面内的兩條直線。隻有兩種情況①平行（無交點）；②相交（有惟一的交點）。
異面直線：即不在同一平面的兩條直線，隻有一種情況，即不平行，也不相交。

公理：平行于同一條直線的兩條直線互相平行（平行線的傳遞性，與a=b，b=c，可知a=c相似）。

定理：空間中如果兩個角的兩邊分别對應平行，那麼這兩個角相等或互補。如圖所示：

高中數學必修2平行關系判斷（高中數學必修二之空間位置關系2）1

二、直線與平面的位置關系：

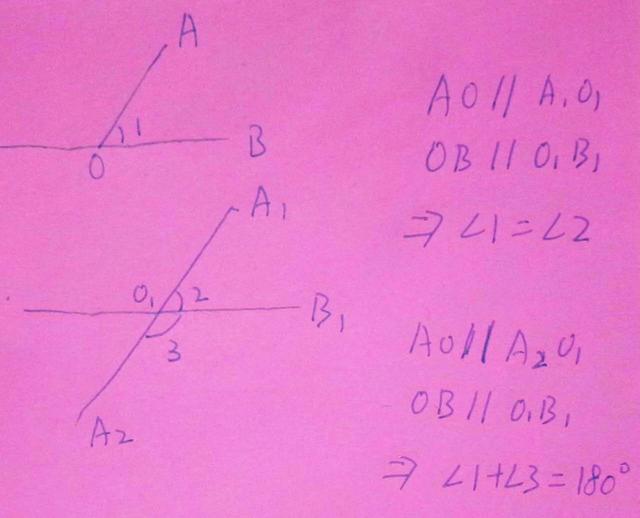
直線與平面的位置分為兩種：㈠直線在平面内（有無數個公共點）

㈡直線在平面外，也可以分為兩種①直線與平面相交（隻有惟一的交點）；②直線與平面平行（沒有公共點）。

如何判定直線與平面平行呢？（前提條件是直線不在平面内）①根據位置關系可知，隻要直線與平面内的一條直線平行，那麼直線與平面平行；②直線與平面沒有公共點，也可以得出直線與平面平行。

定理：一條直線與一個平面平行，則過這條直線的任一平面與此平面的交線與該直線平行。如圖：

高中數學必修2平行關系判斷（高中數學必修二之空間位置關系2）2

今天就分析到這，明天分析平面與平面的位置關系及判定。

輕松一刻：

小明：我給大家講一個笑話，不笑的是狗的兒子。旺旺！！

大家：哈哈哈哈！！！（PS：小明現在輪椅玩的非常溜）

更多精彩资讯请关注tft每日頭條，我们将持续为您更新最新资讯!

查看全部

网友关注

教育學曆真的是一輩子的遺憾嗎
如今的社會——看網絡直播平台興盛、網絡紅人一抓一大把...顔值高好看的明星及時犯錯誤，大量粉絲表明會等他悔過從頭來過，就連刷劇都衍化出了一句“不害怕反派角色壞，就怕反派角色帥”。整容醫療安全事故持續，但仍有大量追求美麗的人前仆後繼........ 2023-04-01
教育高中狀元錯題本怎麼做
幾乎每一年的高考狀元采訪都不約而同地提到了錯題本！我們有時候看着孩子錯題本做得漂漂亮亮，題目謄寫得工工整整，令我們都感歎孩子真愛學習啊？但錯題本到底該怎麼用？今天“大星星愛物理”分享一下我理解的錯題本怎麼用！我們經常看到孩子在同一個知識點甚... 2023-01-14
教育怎麼緩解高考壓力
南都訊7月5日11:00，在廣東省政府新聞辦舉行的第65場疫情防控新聞發布會上，省精神衛生中心心理咨詢科主任尹平，就如何進行最後兩天的高考壓力調節，介紹應對策略。省精神衛生中心心理咨詢科主任尹平（南都記者梁炜培攝）第一，如實面對，高考一定會... 2023-03-30
教育小學數學圓柱與圓錐教學設計
春暖花開，萬木峥嵘。“停課不停學，成長不延期”的居家學習讓我們每天都在感受教學方式的推陳出新，不斷沉澱思考，積聚力量。《圓柱與圓錐》單元學習結束後，六年級數學組的老師們以“巧奪天工，創意無限”為主題開展實踐活動。通過制作圓柱圓錐形體的創意作... 2023-03-21
教育病字的偏旁叫病字旁嗎
一年級我們學習了很多偏旁部首，今天我們來說一下病字頭。疒字，讀nè。筆畫：五筆。筆順：點、橫、撇、點、提。通常，大家把它叫做“病字頭”，因為很多表示疾病的字形都從之釋義：1.倚，靠着。2.病。3.手足麻痹。4.漢字部首之一。5.同“疾”，急... 2023-01-20
教育童繪法制手抄報一等獎
陳瑞澤鹿莊小學五（2）班孫嘉譯湖裡小學四（2）班王乙宇大吳鎮瓦莊小學一（2）吳桂雨西大吳小學五（2）闫梓萌大吳中心小學二（2）佟柯萱大吳中心小學葛雨鑫大吳瓦莊小學一（2）吳紫怡西大吳小學五（3）史曉琪潘安湖小學, 2022-11-19
教育杭州将發二三孩育兒補貼評論
都市快報訊從1982年計劃生育政策成為基本國策，到今年的“三孩”放開，近40年來生育政策變化有什麼趨勢？國家為什麼要放開三孩政策？政策推出後能起到預想效果嗎？群衆最大的呼聲是什麼？一圖看懂我國生育政策變化制圖高薇記者邀請浙江大學社會調查研究... 2023-03-17
教育華少和撒貝甯誰漂亮
何炅可以說是主持界的大佬了，差不多是一哥身份，跟謝娜，杜海濤等人的主持功底對比，何炅真的是相當厲害了。這主要是他的基礎非常好，他早期可是北京外國語大學的教師呢。撒貝甯就更厲害了，北大高材生各種被保送的，他曾說過北大還行，真讓學渣們瞬間覺得紮... 2022-12-25
教育填報志願時本科提前批需要填嗎
又是一年高考季，伴随着緊張的出分時節，不少地區也開始了報志願的艱難抉擇。俗話說：“三分靠靠，七分靠報。”我們由此不難得知高考填報一個好志願的重要性。而此時不少的家長和學子也開始頭疼的狀态：報考志願指南前幾頁的提前批到底是什麼？到底應該不應該... 2023-04-04
教育 21考研新傳專業可以調劑什麼
封面新聞記者何方迪實習生李佳雯今年新聞與傳播專業國家線一出，有人戲谑道：“施拉姆來了都考不上”“麥克盧漢來了都得調劑”，這兩位都是該專業考生必須要了解的人物，也從側面反映出新傳考研難度之高，内卷程度之激烈。教育部公布的2022年考研國家線顯... 2022-12-26
教育給初中家長的十個忠告
給初中家長的十個忠告?，下面我們就來聊聊關于給初中家長的十個忠告?接下來我們就一起去了解一下吧!給初中家長的十個忠告假如可以重來，初中三年我會這樣做家長！中考後一位家長的悔悟...看完這篇文章，你将學到：初一、初二、初三各個階段孩子成績下滑... 2023-04-01
教育 abab式詞語四字成語小學
右上角點擊“關注”，防止丢失，每日更新左上角點擊“頭像”，更多優秀資料等待你們觀看小學成語AABC式、AAB式、ABAB式、ABB式、ABCC式詞語大全，平時讀一讀，寫作詞語不用愁。家長收藏孩子受益。[偷笑]@今日頭條AABC式成語AAB... 2022-12-02
教育一些小學生唱的以假亂真的歌曲
《孤勇者》徹底被全國小學生唱火了，他們人人會唱，而且唱得熱血沸騰。這首歌為何成為時下小學生的熱門單曲？也許就像網友所說的那樣，歌詞裡“沒有技巧，全是感情”。文｜馮玮編輯｜王雅娜本文首發于《時代郵刊》第412期“愛你孤身走暗巷，愛你不跪的模樣... 2022-11-29
教育共享童車能随便放嗎
泉州晚報社·泉州通客戶端1月18日訊（東南早報記者李菁吳嘉曉通訊員張緣文/圖）電動童車是許多孩子喜歡的玩具。近日有家長發現，泉州市區某商場内出現了可掃碼租賃的共享童車。掃碼支付後，孩子們就可以開着車在商場裡暢行無阻。不少家長擔心，孩子在人來... 2022-11-26
教育幼兒流鼻血口裡長泡
記者：王欣/通訊員：李煦轉載請注明來源：杭州交通918從小到大，流鼻血是經常會碰到的情況，大家的普遍操作就是：仰頭，塞紙巾！然而杭州一位媽媽按照這傳統的方法一通操作，孩子居然吐出了一灘“血”！事後，這位媽媽才發現，自己一套全做錯了，“坑娃”... 2022-12-16
教育孩子拒絕寫作業怎麼辦
如果孩子不寫作業，即便被家長打罵也不管用，家長就要轉變教育方式，尤其要做到這三點，分别是向孩子詢問不寫作業的原因、跟孩子強調寫作業的好處、幫助孩子提高寫作業的效率。向孩子詢問不寫作業的原因如果孩子經常不寫作業，家長要跟孩子耐心地溝通，而不是... 2023-01-13
教育研究生學曆平均工資
很多大學生畢業的時候會考慮讀研深造，一來讀研可以提高自己的學曆，将來就業的時候占有優勢，二來現在大環境不好，經濟不樂觀，就業壓力大，沒有太好的崗位就業，通過讀研，達到緩解就業的目的。大家選擇讀研還要一個更重要的想法，提高收入水平，畢竟研究生... 2023-01-05
教育物理必修三第九章靜電場及其應用
高中物理必修三第十章《靜電場中的能量》第二節電勢差，這一節内容其實比前一節提到的電勢更重要，在解決問題中更有意義。一、電勢差的概念：電勢差的概念不難理解，顧名思義，兩個電勢之間的差值。1、電勢差定義：電場中兩點間電勢的差值，也叫電壓。2、對... 2023-01-04
教育給孩子報街舞班需要了解什麼
現在街舞受到越來越多人的關注，很多家長朋友也開始給孩子選擇街舞班當做興趣愛好。學習街舞一方面可以鍛煉身體、強健體魄，另一方面也是一種藝術熏陶、陶冶情操，才藝體育的結合，讓孩子既能夠鍛煉身體也可以掌握一門時尚新潮的藝術，未來在學習生活中都可以... 2023-02-17
教育人教版小學語文古詩知識考點
這是2020年杭州祁績教育發的第137篇頭條文章，以後每天會更新教育類的政策，以及各學科的一些學習技巧、知識點等相關内容，希望大家會喜歡！一起加油，做最好的自己！《敕勒歌》北朝民歌敕勒川，陰山下。天似穹廬，籠蓋四野。天蒼蒼，野茫茫，風吹草低... 2023-03-28
教育小孩如廁訓練需要多長時間
文|兩口育兒（原創文章，歡迎個人轉發、分享）對于新手爸媽來說，什麼是最偉大的發明？紙尿褲絕對是其中一樣！紙尿褲的發明讓新手爸爸媽媽們免去了不斷清洗尿布的煩惱，也更加衛生。要知道小孩子沒辦法控制好自己的如廁時間，紙尿褲簡直是父母帶娃的一大利器... 2023-02-09
教育教師教育的思路是什麼
教師教育的思路是什麼?來源：教師報作者：王平生教師将自己在教育實踐中的心得、感悟、收獲與規律性的東西進一步升華到思想理論高度和科學認識規律的層次，就是提煉教育思想教育家的一個重要特征，就是從長期的教育實踐中不斷提煉自己的教育思想據筆者幾十年... 2023-01-02
教育董卿和謝娜對比
董卿董卿是一名美女學霸，這個從她的主持才華中就可以看出，《詩詞大會》上的她各種詩詞歌賦信手掂來，兼具美貌與内涵。畢業于上海戲劇學院1999屆本科班和華東師範大學2002屆碩士研究生班。上海戲劇學院MFA藝術碩士學位。董卿出生于文化世家，所以... 2022-12-25
教育高考英語寫作中萬能的高分句子
8天長假過去了，是不是還沒有玩夠呢？But，是時候該收心好好學習咯！今天，小編給大家帶來的是有關高考英語寫作的100句經典格言嗯哼，你還在等什麼，快往下看吧！（本文來源：新東方高考）這100句格言不僅可以讓你寫作更加簡單更會讓你通過這些格言... 2023-02-27
教育父母對孩子的教育一定要講究
指責中長大的孩子，将來容易怨天尤人。敵意中長大的孩子，将來容易好鬥逞勇。恐懼中長大的孩子，将來容易畏首畏尾。憐憫中長大的孩子，将來容易自怨自艾。嘲諷中長大的孩子，将來容易消極退縮。嫉妒中長大的孩子，将來容易鈎心鬥角。羞辱中長大的孩子，将來容... 2023-04-01
教育你對幼小銜接了解多少
不同的幼兒園所進行的幼小銜接課程并不相同，而不同的教育理念下發展出來的幼小銜接課程也有很大的差别就拿德培（DAP）理念中的幼小銜接來看德培幼小銜接，是基于國際先進的德培（DAP）理念，依據兒童年齡适宜性、個體适宜性、文化适宜性、教師有效性... 2023-01-03
教育探究式學習的課題研究
2019年2月，州教育體育局下發《關于進一步加強中小學綜合實踐活動課程及研究性學習活動的通知》，提出“以研究性學習培養學生實踐和創新能力”，在全州中小學組織了研究性學習課題研究活動。一年多來，全州各中小學校認真貫徹《通知》要求，組織教師指導... 2022-12-06
教育安徽大學2023屆保研去向
安徽大學是211工程大學。學校的計算機科學與技術學科是國家重點學科。安徽大學互聯網學院成立于2017年，它是安徽大學創新型人才培養和實施“新工科”建設的學院。互聯網學院有六個教學系和一個實驗教學中心，涉及到數據科學與大數據技術、互聯網金融、... 2023-02-25
教育初中生物光合作用呼吸作用公式
光合作用和呼吸作用是初中需要學習的内容，生物雖然不參加中考，但是對初中生來說，我們還是要重視生物，因為會考生物的分數，對中考總成績還是有一定影響的。在光下，植物既進行光合作用合成有機物，也進行呼吸作用分解有機物；無光時，隻進行呼吸作用，消耗... 2023-01-13
教育三年級用鋼筆用什麼樣的筆頭
三年級語文學習，一開始就要面臨一個攔路虎，用要鋼筆寫字了。孩子們很興奮，用鋼筆說明自己語文能力又進了一步；家長們卻很擔憂，新衣服可能到處是墨斑；老師們可能更焦慮，班級衛生可能大受影響不說，作業本上還會到處“濃墨重彩”，那可是整個學期的“面子... 2022-10-20

tft每日頭條

> 教育

> 高中數學必修2平行關系判斷

高中數學必修2平行關系判斷

相关教育资讯推荐

热门教育资讯推荐

网友关注