來源：大數據

本文約12000字，建議閱讀10分鐘。

本文為大家介紹機器學習的魅力與可怕。

[ 導讀 ]作者用超過1.2萬字的篇幅，總結了自己學習機器學習過程中遇到知識點。“入門後，才知道機器學習的魅力與可怕。”希望正在閱讀本文的你，也能在機器學習上學有所成。

00 準備

機器學習是什麼，人工智能的子類，深度學習的父類。

機器學習：使計算機改進或是适應他們的行為，從而使他們的行為更加準确。也就是通過數據中學習，從而在某項工作上做的更好。

引用王钰院士在2008年會議的一句話，假定W是給定世界的有限或者無限的所有對象的集合，Q是我們能夠或得到的有限數據，Q是W的一個很小的真子集，機器學習就是根據世界的樣本集來推算世界的模型，使得模型對于整體世界來說為真。

機器學習的兩個驅動：神經網絡，數據挖掘。

機器學習的分類：

• 監督學習：提供了包含正确回答的訓練集，并以這個訓練集為基礎，算法進行泛化，直到對所有的可能輸入都給出正确回答，這也稱在範例中學習。
• 無監督學習：沒有提供正确回答，算法試圖鑒别出輸入之間的相似，從而将同樣的輸入歸為一類，這種方法稱密度學習。
• 強化學習：介于監督和無監督之間，當答案不正确時，算法被告知，如何改正則不得而知，算法需要去探索，試驗不同情況，直到得到正确答案，強化學習有時稱為伴随評論家的學習，因為他隻對答案評分，而不給出改進建議。
• 進化學習：将生物學的進化看成一個學習過程，我們研究如何在計算機中對這一過程進行建模，采用适應度的概念，相當于對當前解答方案好壞程度的評分。（不是所有機器學習書籍都包含進化學習）

優點：泛化，對于未曾碰到的輸入也能給出合理的輸出。

監督學習：回歸、分類。

機器學習過程：

• 數據的收集和準備
• 特征選擇
• 算法選擇
• 參數和模型選擇
• 訓練
• 評估

專業術語：

• 輸入：輸入向量x作為算法輸入給出的數據
• 突觸：wij是節點i和節點j之間的加權連接，類似于大腦中的突觸，排列成矩陣W
• 輸出：輸出向量y，可以有n個維度
• 目标：目标向量t，有n個維度，監督學習所需要等待額外數據，提供了算法正在學習的“正确答案”
• 維度：輸入向量的個數
• 激活函數：對于神經網絡，g（·）是一種數學函數，描述神經元的激發和作為對加權輸入的響應
• 誤差：E是根據y和t計算網絡不準确性的函數
• 權重空間：當我們的輸入數據達到200維時，人類的限制使得我們無法看見，我們最多隻能看到三維投影，而對于計算機可以抽象出200個相互正交的軸的超平面進行計算，神經網絡的參數是将神經元連接到輸入的一組權重值，如将神經元的權重視為一組坐标，即所謂的權重空間
• 維度災難：随着維度的增加，單位超球面的體積也在不斷增加，2d中，單位超球面為圓，3d中則為求，而更高的維度便稱為超球面，Vn = （2π/n）*Vn-2，于是當n>2π時，體積開始縮小，因此可用數據減少，意味着我們需要更多的數據，當數據到達100維以上時，單位數據變得極小，進而需要更多的數據，從而造成維度災難

維度和體積的關系：

機器學習算法測試：

算法成功程度是預測和一直目标進行比較，對此我們需要一組新的數據，測試集。

當對算法進行訓練時，過度的訓練将會導緻過拟合，即拟合曲線與數據完美拟合，但是失去了泛化能力，為檢測過拟合我們需要用測試集進行驗證，稱為統計中的交叉驗證，它是模型選擇中的一部門：為模型選擇正确的參數，以便盡可能的泛化。

數據的準備，我們需要三組數據集，訓練算法的訓練集，跟蹤算法學習效果的驗證集，用于産生最終結果的測試集，數據充足情況便執行50:25:25或60:20:20的劃分，數據集分配應随機處理，當數據請核實闆塊，則采用流出方法或多折交叉驗證。

混淆矩陣是檢測結果是否良好的分類，制作一個方陣，其包含水平和垂直方向上所有可能的類，在（i，j）處的矩陣元素告訴我們在目标中有多少模式被放入類i中，主對角線上任何東西都是正确答案，主對角線元素之和除以所有元素的和，從而得到的百分比便是精度。

精度指标：真正例是被正确放入類1，假正例是被錯誤放入類1，而真反例是被正确放入類2，假反例是被錯誤放入類2。

真正例（TP）

假正例（FP）

假反例（FN）

真反例（TN）

• 敏感率=#TP/(#TP #FN) 特異率=#TN/(#TN #FP)
• 查準率=#TP/(#TP #FP) 查全率=#TP/(#TP #FN)
• F1 = 2*(查準率*查全率)/(查準率 查全率)

受試者工作曲線：y軸真正例率，x軸假正例率，線下區面積：AUC。

數據與概率的轉換：通過貝葉斯法則處理聯合概率P(C,X)和條件概率P(X|C)得出P(C|X)，MAP問題是訓練數據中最可能的類是什麼。将所有類的最終結果考慮在内的方法稱為貝葉斯最優分類。

損失矩陣：指定類Ci被分為類Cj所涉及的風險。

基本統計概念：協方差，度量兩個變量的依賴程度。

Cov（{xi},{yi}）=E({xi} – u)E({yi} – v)

權衡偏差與方差：偏差-方差困境：更複雜的模型不一定能産生更好的結果；模型糟糕可能由于兩個原因，模型不準确而與數據不匹配，或者不精确而有極大的不穩定性。第一種情況稱為偏差，第二種情況稱為方差。

01 神經元、神經網絡和線性判别

1. 魯棒性

魯棒是Robust的音譯，也就是健壯和強壯的意思。它是在異常和危險情況下系統生存的關鍵。比如說，計算機軟件在輸入錯誤、磁盤故障、網絡過載或有意攻擊情況下，能否不死機、不崩潰，就是該軟件的魯棒性。

2. 神經網絡

神經網絡模仿的便是生物學中的神經網絡，通過輸入進而判定神經元激活否。

将一系列的神經元放置在一起，假設數據存在模式。通過神經元一些已知的樣例，我們希望他能夠發現這種模式，并且正确預測其他樣例，稱為模式識别。為了讓神經網絡能夠學習，我們需要改變神經元的權重和阈值進而得到正确的結果，曆史上的第一個神經網絡——感知器。

3. Hebb法則

突觸連接強度的變化和兩個相連神經元激活得相關性成比例，如果兩個神經元始終同時激活，那麼他們之間連接的強度會變大，反之，如果兩個神經元從來不同時激活，那麼他們之間的連接會消失。也被成為長時效增強法則和神經可塑性。

4. McCulloch和Pitts神經元

建模，一組輸入加權wi相當于突觸，一個加法器把輸入信号相加（等價于收集電荷的細胞膜），一個激活函數，決定細胞對于當前的輸入是否激活，輸入乘于權重的和與阈值進行判斷，大于則激活，否則抑制。局限性：現實中的神經元不給出單一的輸出相應，而是給出一個點位序列，一種連續的方式給出分等級的輸出。神經元不會根據電腦的時鐘脈沖去順序更新，而是随機的異步更新。

5. 感知器

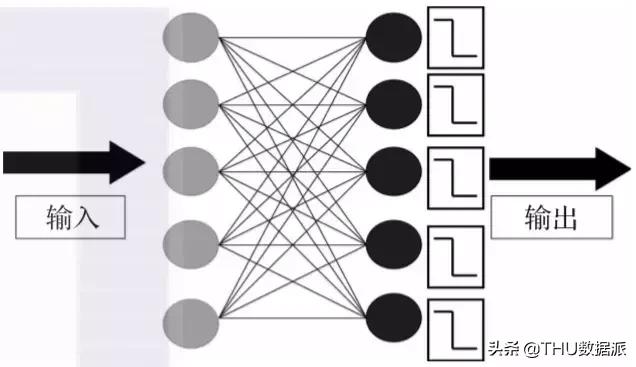
▲感知器神經網絡

• 權重更新規則

Wij <- Wij – n(yi – ti)*xi

N為學習效率，過大會造成網絡不穩定，過小會造成學習時間久；yi為神經元輸出，ti為神經元目标，xi為神經元輸入，Wij為權重。

• 感知器學習算法

分為兩部分，訓練階段和再現階段。

初始化

設置所有的權重wij為小的随機數（正或負都可）。

訓練

對T次循環

對每一個輸入向量：

利用激活函數g計算每一個神經元j的激活狀态：

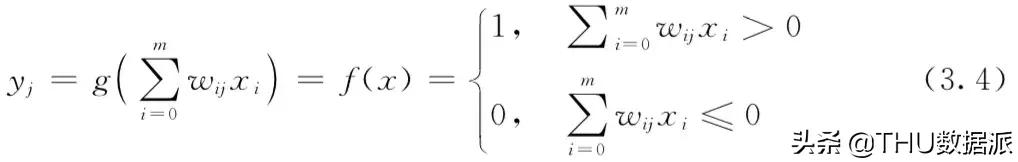
利用下式更新每一個權重：

再現

利用下式計算每一個神經元j的激活狀态：

6. 線性可分性

一條直線将神經元激活的和不激活的神經元劃分開來，這條直線稱為決策邊界，也稱為判别函數，在三維空間該決策邊界為平面，更高維則為超平面。

7. 感知器收斂定理

感知器以1/γ*γ為界，其中γ為分離超平面與最接近的數據點之間的距離。

隻要把數據映射到正确的維度空間，那麼總是可以用一個線性函數來把兩個類别區分開，為了較有效率的解決這個問題，有一整類的方法稱為核分類器，也是支持向量機的基礎。

8. 數據項預處理

特征選擇，我們每次去掉一個不同的特征，然後試着在所得的輸入子集上訓練分類器，看結果是否有所提高，如果去掉某一個特征能使得結果有所改進，那麼久徹底去掉他，在嘗試能否去掉其他的特征，這是一個測試輸出與每一個特征的相關性的過于簡單方法。

9. 線性回歸

回歸問題是用一條線去拟合數據，而分類問題是尋找一條線來劃分不同類别。回歸方法，引入一個指示變量，它簡單的标識每一個數據點所屬的類别。現在問題就變成了用數據去預測指示變量，第二種方法是進行重複的回歸，每一次對其中的一個類别，指示值為1代表樣本屬于該類别，0代表屬于其他類别。

02 維度簡約

1. 降維的三種算法

• 特征選擇法：仔細查找可見的并可以利用的特征而無論他們是否有用，把它與輸出變量關聯起來
• 特征推導法：通過應用數據遷移，即通過可以用矩陣來描述的平移和旋轉來改變圖标的坐标系，從而用舊的特征推導出新的特征，因為他允許聯合特征，并且堅定哪一個是有用的，哪一個沒用
• 聚類法：把相似的數據點放一起，看能不能有更少的特征

2. 特征選擇方法

建設性方法：通過叠代不斷加入，測試每一個階段的錯誤以了解某個特征加入時是否會發生變化。破壞性方法是去掉應用在決策樹上的特征。

• 主成分分析（PCA）

主成分的概念是數據中變化最大的方向。算法首先通過減去平均值來把數據集中， 選擇變化最大的方向并把它設為坐标軸，然後檢查餘下的變化并且找一個坐标軸使得它垂直于第一個并且覆蓋盡可能多的變化。

不斷重複這個方法直到找到所有可能的坐标軸。這樣的結果就是所有的變量都是沿着直角坐标系的軸，并且協方差矩陣是對角的——每個新變量都與其他變量無關，而隻與自己有關。一些變化非常小的軸可以去掉不影響數據的變化性。

• 具體算法

寫成N個點Xi=(X1i，X2i，... xXi)作為行向量。把這些向量寫成一個矩陣X(X将是N*M階矩陣)。通過減去每列的平均值來把數據中心化，并令變化好的矩陣為B。計算協方差陣C= 1/N *B^TB。計算C的特征向量和特征值，即V^-1CV=D,其中V由C的特征向量組成，D是由特征值組成的M*M階對角矩陣。把D對角線上元素按降序排列，并對V的列向量做同樣的排列。去掉那些小于η的特征值，剩下L維的數據。

3. 基于核的PCA算法

選擇核并且把它應用于距離矩陣從而得到矩陣K。計算K的特征值和特征向量。通過特征值的平方根标準化特征向量。保留與最大特征值對應的特征向量。

4. 因素分析

觀察數據是否可以被少量不相關的因素或潛在的變量解釋，目的用于發現獨立因素和測量每一個因素固有的誤差。

5. 獨立成分分析（ICA）

統計成分是獨立的，即對于E[bi,bj] = E[bi]E[bj]與及bi是不相關的。

6. 局部線性嵌入算法

找出每個點的鄰近點(即前k個近的點):計算每對點間的距離。找到前k個小的距離。對于其他點，令Wij=0.對每個點xi:創建一個鄰近點的位置表z,計算zi=zi-xi。

根據約束條件計算令等式（6.31）最小的權矩陣W:計算局部協方差C=ZZ^T，其中Z是zi組成的矩陣。利用CW=I計算W,其中I是N*N單位矩陣。對于非鄰近點，令Wij=0。

對W/∑W設置其他元素計算使得等式(6.32)最小的低維向量 yi:創建M=(I-W)T(I-W).計算M的特征值和特征向量。根據特征值的大小給特征向量排序。對應于第q小的特征值，将向量y的第q行設置為第q 1 個特征向量(忽略特征值為0)

7. 多維标度算法

計算由每對點平方相似度組成的矩陣D, Dij=|xi-xj|.計算J=IN – 1/N (IN是N*N單位矩陣，N是數據點個數)。計算B=-1/2JDJ^T.找到B的L個最大的特征值入i,，以及相對應的特征向量ei。用特征值組成對角矩陣V并且用特征向量組成矩陣P的列向量。計算嵌入x=pv^0.5

8. ISOMAP算法

創建所有點對之間的距離确定每個點的鄰近點，并做成一個權重表G通過找最短路徑估計測地距離dG把經典MDS算法用于一系列dG

03 概率學習

1. 期望最大算法（EM）

額外加入位置變量，通過這些變量最大化函數。

2. 高斯混合模型的期望最大算法

初始化

設置

是從數據集中随機選出來的值

設置

（這裡

是整個數據集的平均值）

設置

=0.5

叠代直到收斂：

3. 通常的期望最大化算法

初始化

猜測參數

叠代直到收斂：

4. 信息準則

除了通過模型選擇确定停止學習的時間，前期采用驗證集思想，而信息準則則是确定一些方法從而期待這個訓練過的模型可以表現的多好。

• 艾卡信息準則：AIC = ln（C）-k
• 貝葉斯信息準則：BIC = 2ln（C）-klnN

K是模型中參數的數目，N是訓練樣本的數量，C是模型的最大似然。以上兩種方法都是奧卡姆剃刀的一種形式。

5. 奧卡姆剃刀

如無必要，勿增實體，即簡單有效原理。

6. 最近鄰法

如果沒有一個描述數據的模型，那麼最好的事情就是觀察相似的數據并且把他們選擇成同一類。

7. 核平滑法

用一個和（一堆點的權重函數）來根據輸入的距離來決定每一個數據點有多少權重。當兩個核都會對離當前輸入更近的點給出更高的權重，而當他們離當前輸入點越遠時，權重會光滑的減少為0，權重通過λ來具體化。

8. KD-Tree

在一個時刻選擇一個維度并且将它分裂成兩個，從而創建一顆二進制樹，并且讓一條直線通過這個維度裡點的坐标的中位數。這與決策樹的差别不大。數據點作為樹的樹葉。

制作樹與通常的二進制樹的方法基本相同：我們定義一個地方來分裂成兩種選擇——左邊和右邊， 然後沿着它們向下。可以很自然地想到用遞歸的方法來寫算法。

選擇在哪分裂和如何分裂使得KD-Tree是不同的。在每一步隻有一個維度分裂，分裂的地方是通過計算那一維度的點的中位數得到的，并且在那畫一條直線。通常，選擇哪一個維度分裂要麼通過不同的選擇要麼随機選擇。

算法向下搜索可能的維度是基于到目前為止樹的深度，所以在二維裡，它要麼是水平的要麼是垂直的分裂。組成這個方法的核心是簡單地選代選取分裂的函數，找到那個坐标的中位數的值，并且根據那個值來分裂點。

04 支持向量機

1. 支持向量機（SVM）

當前現代機器學習中最流行的算法之一，其在大小合理的數據集上經常提供比其他機器學習算法更好的分類性能。

2. 支持向量

在每個類中距離分類線最近的那些點則被稱為支持向量。

如果有一個非線性可分數據集，那麼就不能滿足所有數據點的約束條件，解決方法是引入一些松弛變量η>=0。

3. 選擇核

任何一個對稱函數如果是正定的，都可以用來做核。這就是Mercer定理的結果，Mercer定理也指出一些核旋繞到一起的結果可能是另一個核。

4. 支持向量機算法

初始化：

對于指定的内核和内核參數，計算數據之間距離的内核

這裡主要的工作是計算K=XX^T。

對于線性内核，返回K，對于多項式的次數d，返回1/σ 8 K^d。

對于RBF核，計算K=exp(-(x-x')^2/2σ*σ。

訓練：

将約束集組裝為要求解的矩陣：

約束于

将這些矩陣傳遞給求解器。

将文持向量标識為距高最近點一定距離内的向量,并處理其餘的訓練集。

用公式(8.10)計算b^*

5. 分類

對于給定的測試數據z，使用支持向量對相關内核的數據進行分類，計算測試數據與支持向量的内積，進行分類，返回标記或值。

05 優化和搜索

1. 下山法

朝哪個方向移動才能下降盡可能快：

• 采用線性搜索，知道方向，那麼久沿着他一直走，直到最小值，這僅是直線的搜索；
• 信賴域，通過二次型建立函數的局部模型并且找到這個局部模型的最小值。由于我們不知道防線，因此可以采用貪婪選擇法并且在每個點都沿着下降最快的方向走，這就是所知的最速下降，它意味着pk=-▽f（xk）。最速下降基于函數中的泰勒展開，這是一種根據導數近似函數值的方法。

2. Lenenberg-Marquardt算法

給定一個初始點X0當J^Tr(x)>公差并且沒有超出最大叠代次數:重複:用線性最小二乘法算出(J^TJ vI)dx=一J^Tr中的dx。令Xnew=x dx。計算實際減少和預測減少的比例:實際=||f(x)- f(xnew)||預測=▽f^T(x)*xnew-xp=實際/預測如果0<p<0.25:接受:x=Xnew。或者如果p>0.25:接受: x=Xnew。增加信賴城大小(減少v)。或者:拒絕。減少信賴域大小(增加v)。一直到x被更新或超出跌代的最大次數

3. 共轭梯度

二維空間中，如下圖所示，一步沿x軸方向，另一部沿y方向，這樣足以足以達到最小值。而在n維空間我們應該走n步以達到最小值，它嘗試在線性情況下實現這個想法，但是我們通常感興趣的非線性情況下，隻需要多一點叠代就可以達到最小。

▲左邊：如果方向之間是相互正交的并且步長是正确的，每一個維度隻需要走一步，這裡走了兩步。右邊：在橢圓上共轭的方向不是相互正交的。

具體算法：

給一個初始點x0和停止參數ε,令p0=-▽f(x)。設置Pnew=P0當Pnew>εεp0時:用牛頓-拉夫森叠代法計算αkP當ααdp>ε2時:α=-(▽f(x)^T p)(p^T H(x)p)x=x αPdp=P^TP評價▽f(xnew)。計算βn 1-更新p←▽f(xnew) βk 1p。檢查及重新啟動。

4. 搜索的三種基本方法

• 窮舉法：檢查所有方法，保證找到全局最優
• 貪婪搜索：整個系統隻找一條路，在每一步都找局部最優解。所以對于TSP,任意選擇第-個城市，然後不斷重複選擇和當前所在城市最近并且沒有訪問過的城市，直到走完所有城市。它的計算量非常小，隻有O(NlogN),但它并不保證能找到最優解，并且我們無法預測它找到的解決方案如何，有可能很糟糕。
• 爬山法：爬山法的基本想法是通過對當前解決方案的局部搜索，選擇任一個選項來改善結果，進行局部搜索時做出的選擇來自于一個移動集(moveset)。它描述了當前解決方案如何被改變從而用來産生新的解決方案。所以如果我們想象在2D歐幾裡得空間中移動，可能的移動就是東、南、西、北。

對于TSP，爬山法要先任意選一個解決方案， 然後調換其中一對城市的順序，看看總的旅行距離是否減少。當交換的對數達到預先給定的數時，或找不到一個調換可以改善相對于預先給定的長度的結果時停止算法。

就像貪婪算法一樣，我們無法預測結果将會怎樣：有可能找到全局最優解，也有可能陷在第一個局部最大值上， 從而并不定能找到全局最優解，爬山法的核心循環僅僅是調換對城市， 并且僅當它使得距離變小時才保留調換。

5. 模拟退火算法

開始時選擇一個任意的很高的溫度T，之後我們将随機選擇狀态并且改變它們的值，監視系統變化前後的能量。如果能量變低了，系統就會喜歡這種解決方法，所以我們接受這個變化。目前為止，這和梯度下降法很像。

然而，如果能量不變低，我們仍然考慮是否接受這個解決方法，并且接受的概率是exp((Ebefore- Eafter)/T)。這叫作波爾茲曼分布(Boltzmann distribution)。注意到Ebefore Eafter 是負的，所以我們定義的概率是合理的。偶爾接受這個不好的狀态是因為我們可能找到的是局部最小，并且通過接受這個能量更多的狀态，我們可以逃離出這個區域。

在重複上述方法幾次後，我們采用一個退火時間表以便降低溫度并且使得該方法能延續下去直到溫度達到0。由于溫度變低，所以接受任一個特殊的較高的能量狀态的機會就會變少。最常用的退火時間表是T(l 1)=cT(t)，這裡0<c<1(更加常用的是0.8<c<1)。需要減慢退火的速度以允許更多的搜索。

6. 四種算法TSP結果比較

第一行為最好的解決方案和距離，第二行為運行時間，城市為10個。

Exhaustive search ((1, 5, 10, 6, 3, 9, 2, 4, 8, 7, 0), 4.18) 1781.0613 Greedy search ((3, 9, 2, 6, 10, 5, 1, 8, 4, 7, 0]), 4.49) 0.0057 Hill Climbing ((7, 9, 6, 2, 4, 0, 3, 8, 1, 5, 10]), 7.00) 0.4572 Simulated Annealing ((10, 1, 6, 9, 8, 0, 5, 2, 4, 7, 3]), 8.95) 0.0065

06 進化學習

1. 遺傳算法（GA）

模拟進化是如何搜索的，通過改變基因來改變個體的适應度。

GA使用字符串（類似染色體的作用），字符串中的每個元素都是從某些字母表中選擇，字母表中的值通常是二進制的相當于等位基因，對于解決方法，将被變為一個字符串，然後我們随機生産字符串作為初始種群。

評價适應度可以被看成一個預測，它作用于一個字符串并且返回一個值，它是遺傳算法中唯一因具體問題不同而不同的部分。最好的字符串有最高的适應值，當解決方案不好時，适應度也随之下降，GA工作于由種群組成的字符串，然後評價每個字符串的适應度，并進行培養。

産生後代的常用3種方法：

• 聯賽選擇：反複從種群中挑選四個字符串，替換并将最适合的兩個字符串放人交配池中。
• 截斷選擇：僅按比例f挑出适應度最好的一-部分并且忽略其他的。比如，f= 0.5經常被使用，所以前50%的字符串被放入交配池，并且被等可能地選擇。這很顯然是一個非常簡單的實施方法，但是它限制了算法探索的數量，使得GA偏向于進化。
• 适應度比例選擇：最好的方法是按概率選擇字符串，每個字符串被選擇的概率與它們的适應度成比例。通常采用的函數是(對于字符串a)：

這裡F^α是适應度，如果适應度不是正值，則F需要在整個過程中被exp⁡(sF)替換，這裡s是選擇強度(selection strength)參數，并且你會意識到這個等式作為第4章的softmax激活）：

2. 遺傳算子産生

最常用時實現方法是在字符串中随機找一個點，在這個點之前的部分用字符串1的，而在交叉點之後，用字符串2的剩下部分。我們實際上産生了兩個後代，第2個是由字符串2的第一部分和字符串1的第二部分組成的。這個方式稱為單點交叉，顯然，它的擴展是多點交叉。

最極端的情形是均勻交叉，它的字符串中的每一個元素都随機地選自與他的父母，下圖展示了三中類型的交叉法：

▲交叉算子的不同形式。（a）單點交叉。随機選擇字符串中的一個位置，然後用字符串1的第一部分和字符串2的第二部分組成後代。（b）多點交叉。選擇多個點，後代的生成方式和前面一樣。（c）均勻交叉。每個元素都随機的選自于它的父母。

對當前最好的字符串實現進化通過編譯算子實現，字符串中每個元素的值以概率p（通常很小）改變。

3. 基本遺傳算法

初始化進過我們選的字母表産生N個長為L的字符事。學習生成一個(開始是空的)新的種群。重複： 通過适應度在當前種群中選擇兩個字符串。 重組它們産生兩個新的字符串。 讓後代變異。 要麼把兩個後代加到種群中，要麼使用精英法和比賽法 保持記錄種群中最好的字符串。直到新種群中産生N個字符串可選性地，使用精英法從父代中挑選最合适的字符串，并替換子代中的一些其他字符串。追蹤新種群中最好的字符串。用新種群代替當前種群直到到達停止标準。

4. 使用遺傳算法進行圖着色

把方案編碼成字符串，選擇合适的适應度函數，選擇合适的遺傳算子。

5. 與采樣結合的進化學習

最基礎的版本是我們熟知的基于種群的增長學習算法(PBIL).該算法非常簡單，像基本的GA一樣，它采用一個二進制字母表，但不保留種群，而是利用一個概率向來給出每一個元素是0或1的概率。

起初，向量的每一個值都是0.5，所以每一個元素有相等的機會變成0或1，之後通過從分布指定的向量中取樣來構建群體,并計算群體中每個成員的适合度。

我們使用這個種群中的一個子集(通常隻有前兩個适應度最高的向量)和一個學習速率p來更新概率向量，學習速率通常被設置為0.005(這裡best和second代表種群中最好的和第二好的成員):p= pX(1 - η) η(best十second)/2。

之後丢棄這些種群，并且利用更新的概率向量重新取樣來産生新的種群，算法的核心就是簡單地利用适應度最高的兩個字符串和更多的向量來尋找新的字符串。

07 強化學習

強化學習是狀态(state)或情形(situation)與動作(action)之間的映射，目的是最大化一些數值形式的獎賞(reward)。也就是說，算法知道當前的輸人(狀态)，以及它可能做的一些事(動作)，目的是最大化獎賞。進行學習的智能體和環境之間有着明顯的區别，環境是智能體完成動作的地方，也是産生狀态和獎賞的地方。

1. 馬爾可夫決策過程

馬爾可夫性：當前的狀态對于計算獎賞提供了足夠的信息而不需要以前的狀态信息，一個具有馬爾可夫性的強化學習成為馬爾可夫決策過程。它意味着基于以前的經曆，我們隻需要知道當前的狀态和動作就可以計算下一步獎賞的近似，以及下一步的狀态。

2. 值

強化學習嘗試決定選擇哪一個動作來最大化未來的期望獎賞，這個期望獎賞就是值，可以考慮當前狀态，對所有采取的動作進行平均，讓策略來自己解決這個問題，即狀态值函數，或者考慮當前狀态和可能采取的動作即動作值函數。

3. O-learning算法

初始化對于所有的s和a, 設置Q(s, a)為一個很小的随機數。重複:初始化s。用目前的策略選擇動作a。重複： 使用ε-greedy或者其他策略來選擇動作a。 采取動作a并得到獎賞r。 采樣新的狀态s’ 更新Q(s, a)←Q(s, a) u(r γmaxa’ (s', a')-Q(s, a)) 設置s←s'應用到當前情節的每一步。直到沒有更多的情節。

4. Sarsa算法

初始化對于所有的s和a,設置Q(s, a)為一個很小的随機數。重複:初始化s。用當前策略選擇動作重複: 實行動作a并得到獎賞r 采樣新的狀态s' 用當前策略選擇動作a 更新Q(s, a)<-Q(s, a) u(r yYQ(s',a')-Q(s,a)). s<-s’,a<-a’應用到當前情節的每一步直到沒有更多的情節。

• 兩種算法的相同

都是bootstrap方法，因為他們都是從對正确答案很少的估計開始，并且在算法進行過程中不斷叠代。

• 不同

兩個算法一開始都沒有環境的任何信息，因此會利用ε-greedy策略随機探索。然而，随着時間的推移，兩個算法所産生的決策出現了很大的不同。

産生不同的主要原因是Q-learning總是嘗試跟着最優的路徑，也就是最短的路，這使它離懸崖很近。并且，ε-greedy也意味着有時将會不可避免地翻倒。通過對比的方式，sarsa 算法将會收斂到一個非常安全的路線，它遠離懸崖，即使走的路線很長。

sarsa 算法産生了一個非常安全的路線，因為在它的Q的估計中包含了關于動作選擇的信息，而Q-learning生成了一條冒險但更短的路線。哪種路線更好由你決定，并且依賴于跌落懸崖的後果有多麼嚴重。

08 樹的學習

決策樹的主要思想是從樹根開始，把分類任務按順序分類成一個選擇，一步步進行到葉子節點最終得到分類的結果，樹結構可以表示成if-then規則的集合，适合應用于規則歸納系統。

1. ID3

在決策樹下一次分類是，對于每一個特征，通過計算真個訓練集的熵減少來選擇特征，這成為信息增益，描述為整個集合的熵減去每一個特定特征被選擇後的熵減去每一個特定特征被選中後的熵。

• 具體算法

如果所有的樣本都具有同一标記:返回标記為該類标記的葉子節點。否則，如果沒有剩餘特征用于測試:返回标記為最常見标記的葉子節點，否則:使用公式選擇S中具有最大信息增益的特征戶作為下一個節點。為每一個特征戶的可能取值f增加一個分支。對于每個分支:計算除去F後的每一個特征的Sf，使用Sf遞歸調用算法，計算目前樣本集合的信息增益。

• 決策樹複雜度

假設樹是近似平衡的，那麼每個節點的成本包括搜索d個可能的特征（盡管每個層級減少1，但這不會影響O(·)符号的複雜性），然後計算每個分裂的數據集的信息贈與，這需要花費O（dnlogn），其中n為該節點上數據及的大小，對于根節點，n=N，并且如果樹是平衡的，則在樹的每個階段将n除于2。在樹種的大約logN層級上對此求和，得到計算成本O(dN^2logN)。

09 委員會決策：集成學習

下圖為集成學習的基本思想，給定一個相對簡單的二類分類問題和一些學習器，一個學習器的橢圓覆蓋數據的一個子集，組合多個橢圓給出相當複雜的決策邊界。

▲通過組合許多簡單的分類器（這裡簡單地将橢圓決策邊界放在數據上），決策邊界可以變得更加複雜，使得正例與圓圈難以分離。

1. AdaBoost（自适應提升）

每次叠代中，一個新的分類器在訓練集上訓練，而訓集中的每-個數據點在每一步叠代時都會調整權重，改變權重的根據是數據點被之前的分類器成功分類的難度。一開始， 這些權重都被初始化為1/N,其中N是訓練集中點的個數然後，每次叠代時，用所有被錯分的點的權重之和作為誤差函數ε。

對于錯誤分類的點，其權重更新乘子為a=(1-ε)/ ε。對于正确分類的點，其權重不變。接着在整個數層集上做歸一化(這是降低被正确分類的數據點的重要性的有效方法)。在設定的叠代次數結束之後訓練終止，或者當所有的數據點都被正确分類後訓練終止，或者一個點的權重大于最大可用權重的一半時訓練也終止。

具體算法：

初始化所有的權值為1/N，其中N為數據點的個數

當

(t<T,最大叠代次數)：

在

上訓練分類器，得到數據點

的假設

計算訓練誤差

設置

使用如下公式更新權值：

其中Zn為标準化常量

返回标記為最普通類标的葉子節點

2. 随機森林

如果一棵樹是好的，那麼許多樹木應該更好，隻要他們有足夠的變化。

3. 基本的随機森林訓練算法

對于每N個樹:創建一個訓練集的bootstrap樣本。使用這個bootstrap樣本訓練決策樹。在決策樹的每一個節點，随機選擇m個特征，然後隻在這些特征集合中計算信息增益(或者基尼不純度)，選擇最優的一個。重複過程直到決策樹完成。

4. 專家混合算法

對于每一個專家：

計算屬于每一個可能的類别的輸入的概率，通過如下公式計算（其中w_i是對于每個分類器的權重）：

對于樹上的每個門控網絡：

計算：

傳遞一個輸入到下一層門（這裡的和是和該門相關的輸入上的和）：

10 無監督學習

無監督學習在不知道數據點屬于這一類而那些數據點屬于另一類的情況下找到數據中相似輸入的簇。

1. k-means算法

初始化

選擇一個k值。

在輸入空間中選擇k個随機位置。

将簇中心μj,安排到這些位置。

學習

重複:

對每一個數據點Xi:

計算到每一個簇中心的距離。

用下面的距離将數據點安排到最近的簇中心。

對每個簇中心:

将中心的位置移到這個簇中點的均值處(Nj是簇j中點的個數):

直到簇中心停止移動

使用

對每個測試點:

計算到每個簇中心的距離。

用下面的距離将數據點安排到最近的簇中心

2. 在線k-Means算法

初始化

選擇一個值k,它與輸出節點的數目有關。

用小的随機值來初始化權重。

學習

歸一化數據以便所有的點都在單位球上。

重複:

對每一個數據點:

計算所有節點的激活。

選出激活最高的那個節點作為勝利者。

用公式更新權重。

直到叠代的次數超過阈值。

使用

對于每個測試點：

計算所有節點的激活

選擇激活最高的節點作為勝利者

3. 自組織特征映射算法

初始化

選擇大小（神經元數目）和映射的維度d

或者

随機選擇權重向量的值使得它們都是不同的OR

設置權值來增加數據的前d個主成分的方向

學習

重複

對每一個數據點：

用權重和輸入間的歐氏距離的最小值來選擇最匹配的神經元

，

用下面的公式來更新最匹配節點的權重向量：

這裡η(t)是學習效率

其他的神經元用下面的公式更新權重向量：

這裡

是鄰居節點的學習效率，而是鄰居函數

，它決定是否每個神經元應該是勝利神經元的鄰居（所以h=1是鄰居，h=0不是鄰居）

減少學習效率并且調整鄰居函數，一般通過

，這裡0≤α≤1決定大小下降的速度，k是算法已經運行的叠代次數，k_max是算法停止的叠代次數。相同的公式被用于學習效率(η,ηn)和鄰居函數

直到映射停止改變或超出了最大叠代的次數

使用

對每個測試點：

用權重和輸入間的歐氏距離的最小值來選擇最匹配的神經元n_b：

編輯：黃繼彥

— 完 —

關注清華-青島數據科學研究院官方微信公衆平台“THU數據派”及姊妹号“數據派THU”獲取更多講座福利及優質内容。

,

更多精彩资讯请关注tft每日頭條，我们将持续为您更新最新资讯!

查看全部