導數的結果應該是嚴格的特定的0/0——如歐拉所言（3）（續2017-7-3文章）

3 從圖象看dy／dx=(0／0)…的真谛

現在我們根據求導運算的圖像中讨論求導運算。這樣更直觀、更明确。

3.1 幾何含義——在點處才是準确值

為了更進一步理解最終dy ／dx =(0／0)=…

，的含義，讓我們結合y=ax^2（“^”表示乘方）的圖象，看一看導數的幾何意義。

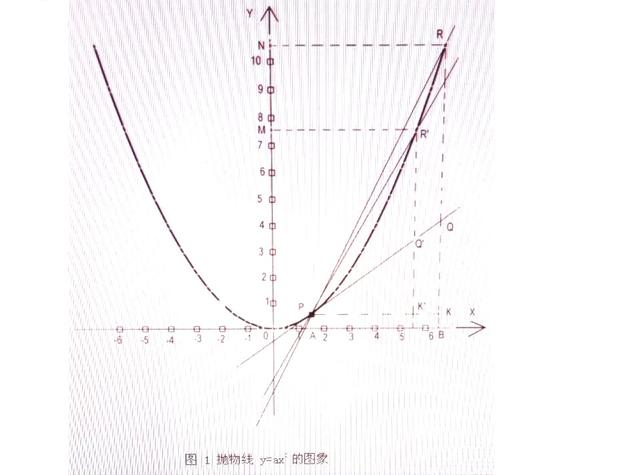
圖1 抛物線y=ax2的圖象

如圖１所示，顯然，Δy=RK，Δx=PK。PQ為過點P的曲線y=ax^2的切線。這條切線的存在是顯然的，不應該回避。

P點乃是原函數上的普通一點，但也因此而具有代表性。于是如果這一點不予考慮，即它的導數不予考慮，則其它點的導數亦無從考慮。那導數存在于何處呢？

（3.1.5）

成立的條件仍然僅僅是而且必須是最終Δx=0。而aΔx則是當Δx≠0才存在，它表示在Δx≠0的時候割線的斜率與導數的準确值的誤差。

于是從導數的幾何含義和數值運算這兩個角度考察後，結論都是應該承認2ax才是原函數裡隐含着的新關系中的有意義的項。

牛頓也曾經從幾何直觀的角度認為，隻有在割線變成切線時，才求出了導數的準确值。他還說，“在數學中即使是最微小的誤差也不應忽略。”[17]可見數學直觀有時是很有用的。（可惜他沒有堅持到底。當然不應該苛求。）

還可以看出，△y/△x是具有數學含義的，它表示在〔x,x Δx〕的區間内，函數值的平均變化率。這是一個新的質，但是它目前還不是準确值，而是近似值，是預備狀态的值（請讀者注意，現在我們已經不是從“外邊”研究函數了，我們的研究已經逐漸進入到函數的“内部”了。我們要研究的是函數的變化率。恩格斯曾經指出，求導運算是“在函數内部”研究變化。[18]這是很正确、很深刻的。）

顯然在這整個區間内都有Δy随Δx的改變而改變的依賴關系，于是△y/△x的極限即新的質dy/dx在每一點處都存在，并且有相應的值，就是毫無疑義的。更一般的說，這個新關系——原函數中隐含着的新關系——在整個可導函數的整個曲線上都存在。

3.2 Δx和Δy趨向的是各自的0，不是相同的0

從圖１中還可以看出，Δy=RK，Δx=PK，而我們求導運算的出發點是：

△y/△x =RK／PK=2ax aΔx （3.2.1）

但是不難理解過P、R兩點的可導函數的曲線有無數條，顯然對這些函數而言，它們的

△y/△x都是相同的：

△y/△x =RK／PK （3.2.2）

但是它們的右邊則顯然随原函數的不同而不同，即是特定的近似。（我們又一次發現，在Δx≠0時，△y/△x确是近似值。）

于是隻有在R沿着圖中的抛物線逐漸逼近并且在最終到達P點的時候，割線PR才終于成為該抛物線的切線PQ。此時Δx=0是顯然的。

而且也容易看出，此時的Δy也等于0。

但是此時的Δy卻不一定等于此時的Δx。從圖象中可以看出，此時的△y/△x乃是抛物線在P點的切線PQ與X軸的夾角的斜率。這個數值在一般情況下是不等于1的，隻有在很特殊的情況下才等于1。

現在我們可以下結論了：在求導運算的最後結果中，認為Δx=0的意見才是正确的。

3.3 數學界應該接受最終的△y/△x =0/0的結果

那為什麼數學家竟然讨論了三百多年，卻至今仍然沒有接受這個結論呢？困難在哪裡呢？困難在于：若

Δx=0， （3.3.1）

即

x1=x， （3.3.2）

則

y1=f(x1)=f(x)=y， （3.3.3）

于是這時

Δy=0。

即在當極限limΔx=0時，（1.6）式應該是：

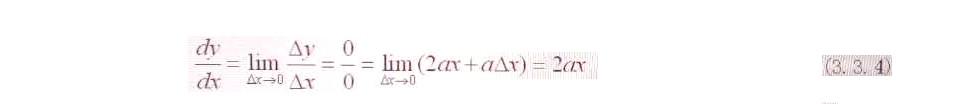
(3.3.4)

（3.3.4）式當然也是我們所強調的導數的最終結果。可是令人吃驚的是，其中分母竟然變成了零，分子也是零，可是(0／0)竟又等于一個确定的數。這是怎麼回事？怎麼辦？

有辦法。

（未完待續）

更多精彩资讯请关注tft每日頭條，我们将持续为您更新最新资讯!