本題來自于四川成都,位于選擇題第12題問題

在函導數這裡取對數的思想是非常常見的思想,例如指數的求導等,取對數放縮更是非常常見的數學思想,學生要具備這樣的數學能力,最開始接觸取對數思想始于高一階段對數和指數互換一節,但是我們在教學時忽略了思想的跟進和知道,使得很多同學到高二和高三做導數題時思想接受不高,甚至很陌生。
我們學習要學會歸納法和推演法兩種研究問題的思想,新課不能丢的環節,這是練習學生具備解決問題方法的能力的平台,新課要充分體現這兩種方法,隻有學生具備解決問題的能力,才能算作高水平的孩子。
方法一:取對數切線放縮法
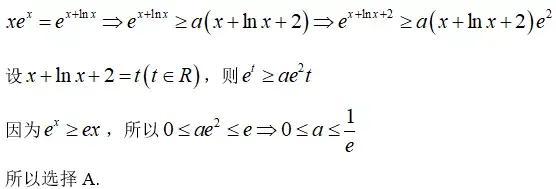
方法點評:
本題用到了①取對數的數學思想;②切線放縮,切線放縮法是18世紀牛頓先生創建并運用起來,尤其在解決代數問題有着強大的生命力,但是換元的取值範圍這個要及時的求出,這關乎函數的連續性問題的讨論,函數的連續性在微積分中是重中之重,這也是求新自變量範圍(連續性)的重要性。
,更多精彩资讯请关注tft每日頭條,我们将持续为您更新最新资讯!




