今天是算法數據結構專題的第34篇文章，我們來繼續聊聊最短路算法。

　　在上一篇文章當中我們講解了bellman-ford算法和spfa算法，其中spfa算法是我個人比較常用的算法，比賽當中幾乎沒有用過其他的最短路算法。但是spfa也是有缺點的，我們之前說過它的複雜度是O(kE)，這裡的E是邊的數量。但有的時候邊的數量很多，E最多能夠達到V^2，這會導緻超時，所以我們會更換其他的算法。這裡說的其他的算法就是Dijkstra。

　　算法思想 在上一篇文章當中我們曾經說過Bellman-ford算法本質上其實是動态規劃算法，我們的狀态就是每個點的最短距離，策略就是可行的邊，由于一共最多要松弛V-1次，所以整體的算法複雜度很高。當我們用隊列維護可以松弛的點之後，就将複雜度降到了O(kE)，也就是spfa算法。

　　Dijkstra算法和Bellman-ford算法雖然都是最短路算法，但是核心的邏輯并不相同。Dijkstra算法的底層邏輯是貪心，也可以理解成貪心算法在圖論當中的使用。

　　其實Dijstra算法和Bellman-ford算法類似，也是一個松弛的過程。即一開始的時候除了源點s之外，其他的點的距離都設置成無窮大，我們需要遍曆這張圖對這些距離進行松弛。所謂的松弛也就是要将這些距離變小。假設我們已經求到了兩個點u和v的距離，我們用dis[u]表示u到s的距離，dis[v]表示v的距離。

　　假設我們有dis[u] dis[v]，也就是說u離s更近，那麼我們接下來要用一個新的點去搜索松弛的可能，u和v哪一個更有可能獲得更好的結果呢？當然是u，所以我們選擇u去進行新的松弛，這也就是貪心算法的體現。如果這一層理解了，算法的整個原理也就差不多了。

　　我們來整理一下思路來看下完整的算法流程：

　　我們用一個數組dis記錄源點s到其他點的最短距離，起始時dis[s] = 0，其他值設為無窮大我們從未訪問過的點當中選擇距離最小的點u，将它标記為已訪問遍曆u所有可以連通的點v，如果dis[v] dis[u] l[u] [v]，那麼更新dis[v]重複上述2，3兩個步驟，直到所有可以訪問的點都已經訪問過 怎麼樣，其實核心步驟隻有兩步，應該很好理解吧？我找到了一張不錯的動圖，大家可以根據上面的流程對照一下動圖加深一下理解。

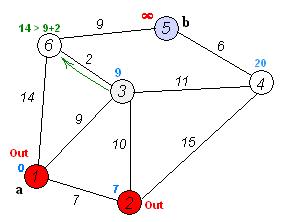
　　我們根據原理不難寫出代碼：

　　INF=sys.maxsize edges=[[]]#鄰接表存儲邊 dis=[]#記錄s到其他點的距離 visited={}#記錄訪問過的點 whileTrue: mini=INF u=0 flag=False #遍曆所有未訪問過點當中距離最小的 foriinrange(V): ifinotinvisitedanddis[i]mini: mini,u=dis[i],i flag=True #如果沒有未訪問的點，則退出 ifnotflag: break visited[u]=True forv,linedges[u]: dis[v]=min(dis[v],dis[u] l)

　　雖然我們已經知道算法沒有反例了，但是還是可以思考一下。主要的點在于我們每次都選擇未訪問的點進行松弛，有沒有可能我們松弛了一個已經訪問的點，由于它已經被松弛過了，導緻後面沒法拿來松弛其他的點呢？

　　其實是不可能的，因為我們每次選擇的都是距離最小的未訪問過的點。假設當前的點是u，我們找到了一個已經訪問過的點v，是不可能存在dis[u] l dis[v]的，因為dis[v]必然要小于dis[u]，v才有可能先于u訪問。但是這有一個前提，就是每條邊的長度不能是負數。

　　算法優化 和Bellman-ford算法一樣，Dijkstra算法最大的問題同樣是複雜度。我們每次選擇一個點進行松弛，選擇的時候需要遍曆一遍所有的點，顯然這是非常耗時的。複雜度應該是O(V^2 E)，這裡的E是邊的數量，Dijkstra中每個點隻會松弛一次，也就意味着每條邊最多遍曆一次。

　　我們觀察一下會發現，外面這層循環也就算了，裡面這層循環很沒有必要，我們隻是找了一個最值而已。完全可以使用數據結構來代替循環查詢，維護最值的場景我們也已經非常熟悉了，當然是使用優先隊列。

　　使用優先隊列之後這段代碼會變得非常簡單，同樣也不超過十行，為了方便同學們調試，我把連帶優先隊列實現的代碼一起貼上來。

　　importheapq importsys #優先隊列 classPriorityQueue: def__init__(self): self._queue=[] self._index=0 defpush(self,item,priority): #傳入兩個參數，一個是存放元素的數組，另一個是要存儲的元素，這裡是一個元組。 #由于heap内部默認由小到大排，所以對priority取負數 heapq.heappush(self._queue,(-priority,self._index,item)) self._index =1 defpop(self): returnheapq.heappop(self._queue)[-1] defempty(self): returnlen(self._queue)==0 que=PriorityQueue() INF=sys.maxsize edges=[[],[[2,7],[3,9],[6,14]],[[1,7],[3,10],[4,15]],[[1,9],[2,10],[6,2],[4,11]],[[3,11],[5,6]],[[4,6],[6,9]],[[3,2],[5,9]]]#鄰接表存儲邊 dis=[sys.maxsizefor_inrange(8)]#記錄s到其他點的距離 s=1 que.push(s,0) dis[s]=0 visited={} whilenotque.empty(): u=que.pop() ifuinvisited: continue visited[u]=True forv,linedges[u]: ifvnotinvisitedanddis[u] ldis[v]: dis[v]=dis[u] l que.push(v,dis[v]) print(dis)

　　這裡用visited來判斷是否之前訪問過的主要目的是為了防止負環的産生，這樣程序會陷入死循環，如果确定程序不存在負邊的話，其實可以沒必要判斷。因為先出隊列的一定更優，不會存在之後還被更新的情況。如果想不明白這點加上判斷也沒有關系。

　　我們最後分析一下複雜度，每個點最多進入隊列一次，加上優先隊列的調整耗時，整體的複雜度是

　　O(VlogV E)，比之前V^2 E的複雜度要提速了很多，非常适合邊很多，點相對較少的圖。有時候spfa卡時間了，我們會選擇Dijkstra。

　　今天的文章到這裡就結束了，如果喜歡本文的話，請來一波素質三連，給我一點支持吧（關注、轉發、點贊）。

　　本文始發于公衆号：TechFlow，求個關注

　　,

更多精彩资讯请关注tft每日頭條，我们将持续为您更新最新资讯!