作者:y1600108
關于目前wows的炮擊散布,已知的一共有以下幾個參數:
以上是對已有參數的總結,接下來提出我的猜想:
一發炮彈軌迹的生成,從開始到結束的過程如下:

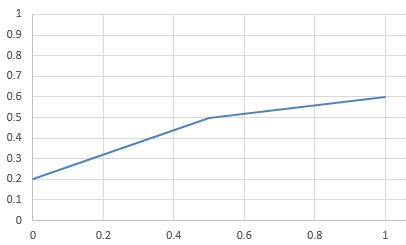
一些說明:
精美 圖例
由于測量落點太過麻煩(錄屏後找出每次落點水花的圓心,沒有太多技術含量但是機械重複次數太多),感覺我個人沒法抽時間完成大量的實驗工作,故上述理論還隻是停留在猜想的階段,隻能由上述理論來畫一些圖例,看起來跟我個人體感還挺符合的(
以下的散布展示中,每一圈代表10%的概率,大概能表現不同sigma和縱向系數影響下的散步集中程度
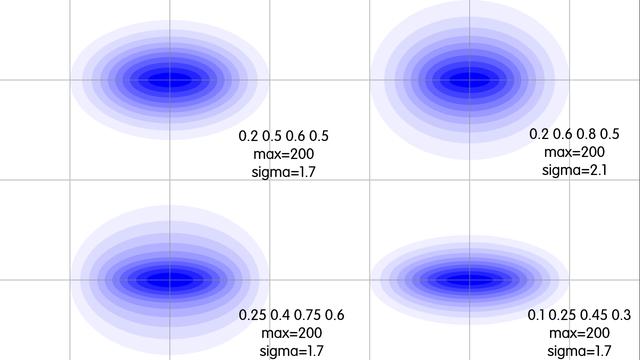



關于我這個理論的驗證方法,其實很簡單,就是記錄落點,與以上的圖例進行比對,但是一般而言一組落點樣本至少要有五百個吧,所以也很難得弄就是了(這也是你遊散布一直沒人研究的最大原因:規模足夠的實驗太難做了)

更多精彩资讯请关注tft每日頭條,我们将持续为您更新最新资讯!




