二次根式的化簡與求值

【閱讀與思考】

1.二次根式的化簡與求值問題常涉及最簡根式、同類根式，分母有理化等概念，常用到分解、分拆、換元等技巧.

2.有條件的二次根式的化簡與求值問題是代數變形的重點，也是難點，這類問題包含了整式、分式、二次根式等衆多知識，又聯系着分解變形、整體代換、一般化等重要的思想方法，解題的基本思路是:

(1)、直接代入

直接将已知條件代入待化簡求值的式子.

(2)、變形代入

适當地變條件、适當地變結論，同時變條件與結論，再代入求值.

【數學思想】

數學中充滿了矛盾，如正與負，加與減，乘與除，數與形，有理數與無理數，常量與變量、有理式與無理式，相等與不等，正面與反面、有限與無限，分解與合并，特殊與一般，存在與不存在等，數學就是在矛盾中産生，又在矛盾中發展.

【例題與求解】

【點評】

此題考查二次根式的化簡求值，充分利用已知條件是關鍵，還要注意整體思想的應用.

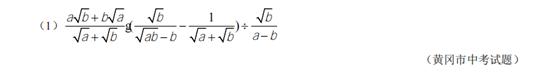
【點評】

本題考查了二次根式的化簡求值:二次根式的化簡求值，一定要先化簡再代入求值.二次根式運算的最後，注意結果要化到最簡二次根式，二次根式的乘除運算要與加減運算區分，避免互相幹擾.也考查了分式的混合運算.

【點評】

本題考查了二次根式的混合運算:先把各二次根式化為最簡二次根式，再進行二次根式的乘除運算，然後合并同類二次根式.

【點評】

根據“提示”，将原式的分子拆項變形，進而把原式變為兩個代數式的和，約分、分母有理化計算即可.

【解析】

把分子分母利用因式分解的方法變形，然後約分即可.

【點評】

本題考查了二次根式的計算:先把各二次根式化為最簡二次根式，再進行二次根式的乘除運算，然後合并同類二次根式.在二次根式的混合運算中，如能結合題目特點，靈活運用二次根式的性質，選擇恰當的解題途徑，往往能事半功倍.

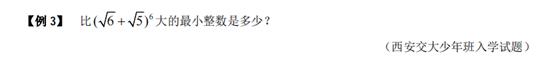
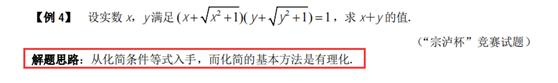
【點評】

本題考查了函數的值的求法，本題的關鍵是設而不求，屬于中檔題

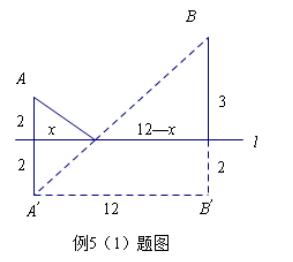
【解析】

1.本題考查的是最短線路問題，把求代數式的最小值轉化為最短線路問題，利用數形結合解答是解答此類問題的關鍵.

2.解決問題時需要注意其中涉及的計算問題，仔細計算，切忌馬虎大意，本題屬于難題，同學們要認真審題.

【解析】

先根據完全平方公式化簡m并求出m的值，再把m的值代入，運用等比數列的求和公式得出結果.

【點評】

本題考查了二次根式的化簡，完全平方公式的應用及等比數列的求和公式.屬于競賽題目，有一定難度.注意求m的值時，看清字母a的取值範圍.

更多精彩资讯请关注tft每日頭條，我们将持续为您更新最新资讯!