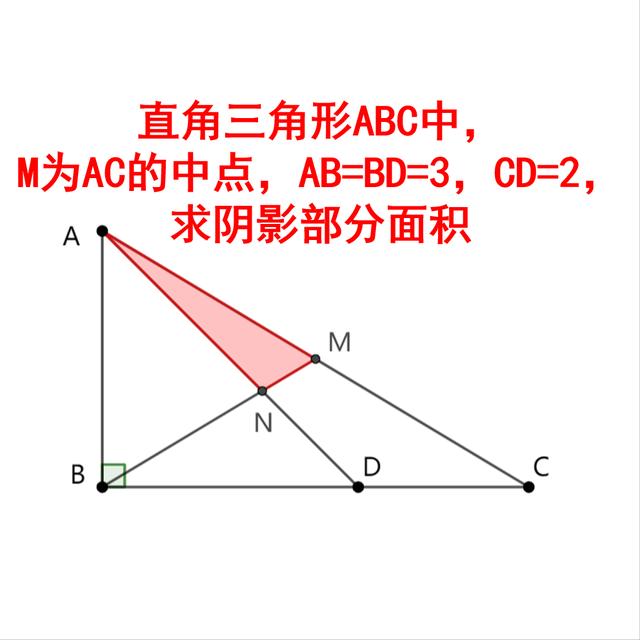
題目：

直角三角形ABC中，M為AC的中點，AB=BD=3，CD=2，求陰影部分面積

知識點回顧：

1. 直角三角形兩直角邊的平方和等于斜邊的平方。（勾股定理)
2. 在直角三角形中，兩個銳角互餘。
3. 直角三角形中，斜邊上的中線等于斜邊的一半（即直角三角形的外心位于斜邊的中點，外接圓半徑R=C/2）。該性質稱為直角三角形斜邊中線定理。
4. 直角三角形的兩直角邊的乘積等于斜邊與斜邊上高的乘積。
5. Rt△ABC中，∠BAC=90°，AD是斜邊BC上的高，則有射影定理如下：（AD)²=BD·DC；（AB)²=BD·BC；（AC)²=CD·BC。

1. 判定1：有一個角為90°的三角形是直角三角形。
2. 判定2：若a² b²=c²，則以a、b、c為邊的三角形是以c為斜邊的直角三角形。
3. 判定3：若一個三角形30°内角所對的邊是某一邊的一半，則這個三角形是以這條長邊為斜邊的直角三角形。
4. 判定4：兩個銳角互為餘角（兩角相加等于90°）的三角形是直角三角形。
5. 判定5：若兩直線相交且它們的斜率之積互為負倒數，則兩直線互相垂直。那麼這個三角形為直角三角形。
6. 判定6：若在一個三角形中一邊上的中線等于其所在邊的一半，那麼這個三角形為直角三角形。

1. 對應角相等；
2. 對應邊成比例；
3. 相似三角形的周長比等于相似比；
4. 相似三角形的面積比等于相似比的平方。

1. 兩角對應相等，兩個三角形相似。
2. 兩邊對應成比例且夾角相等，兩個三角形相似。
3. 三邊對應成比例，兩個三角形相似。
4. 三邊對應平行，兩個三角形相似。
5. 斜邊與直角邊對應成比例，兩個直角三角形相似。
6. 全等三角形相似。

1. 相似圖形，面積比等于對邊比的平方也就是S1：S2=a^2/b^2
2. S1:S2:S3:S4= a²:b²:ab:ab ；S1:S3=S4:S2
3. S3=S4
4. S1×S2=S3×S4(由S1/S3=S4/S2推導出)
5. AO:OC=(S1 S3):(S2 S4)

粉絲解法1：

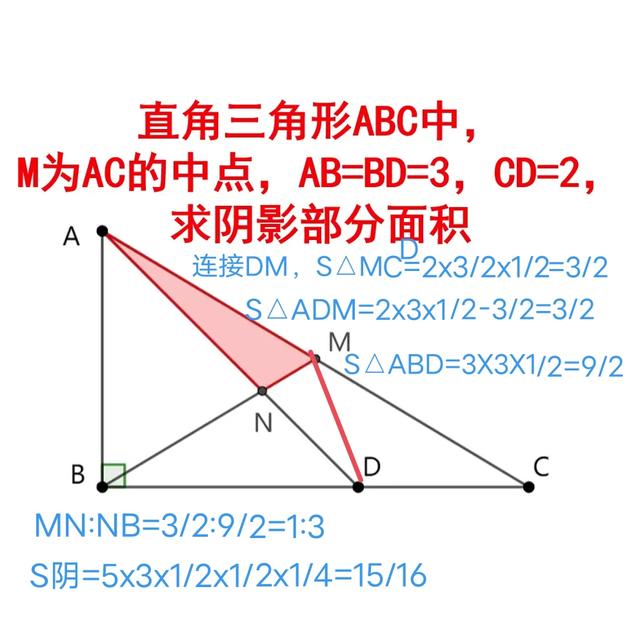
粉絲解法2：

∵M是中點，∴a d=a b c=15/4又c d=9/2 ,b 2a=3解得:a=15/16

粉絲解法3：

解：AB=3 BC=3 2→S△ABC=15/2過點M作ME∥BC交AD于E M是BC中點→EM∥DC→EM=1 EM∥BD→△EMN∽△DBN→EM/BD=MN/BN=1/3 S△ABM=15/4→S陰影=15/16

粉絲解法4：

如圖，連接CN，設S△AMN＝a，S△CDN＝2b，由題意可知: 其他三角形面積如圖所标，S△ABD＝8b＝9/2b＝9/16, S△ABC＝5/3·S△ABD＝15/2S△AMB＝S△ABC/2＝15/4S陰影＝15/4—5b＝15/16

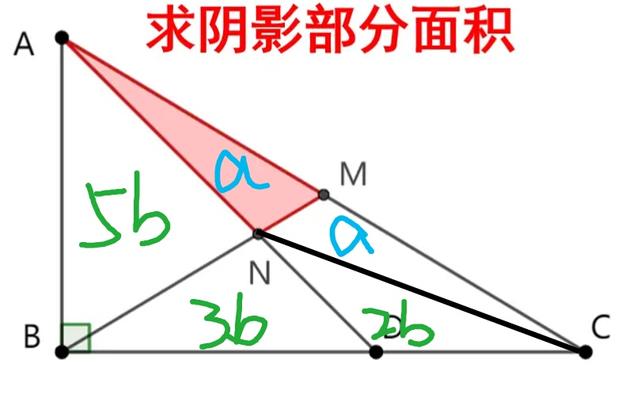
粉絲解法5：

MN:BN=2×3/2/2):(3×3/2=1：3，S陰=ABM/4=5x3/2/2/4=15/16(平方厘米)

粉絲解法6：

連接CN，設三角形AMN面積=三角形CMN面積，設為a，三角形CDN面積為2b，三角形BDN面積為3b，三角形ABN面積為5b，三角形ABD面積=8b=9/2，b=9/16,三角形ACD面積 =2a 2b=3*2/2，a=15/16，陰影面積=15/16。

粉絲解法7：

粉絲解法8：

由BD/DC*CA/AM*MN/NB=1得MN/BM=1/4陰影面積=3*5/2/4/2=15/16

粉絲解法9：

分享個不同思路，最近輔導小朋友，習慣用坐标系解法，此題轉換成知道N點坐标，即可求解了。 M（2.5,1.5），AD（y=-x 3），BM（y=3/5x）函數圖像都很簡單能夠直接看出來，然後計算交點N的X坐标為15/8，陰影面積就是高差(2.5-15/8)xAB/2 =15/16。

粉絲解法10：

粉絲解法11：

解：連結Nc，設S△ANM為a S△DNc為b，則： ∵AM＝MC，BD：Dc＝3：2 ∴S△NcM＝S△ANM＝a S△BND＝1.5S△DNC＝1.5b S△ABM＝S△Bcm＝a＋2.5b S△ABN＝2.5b S△ABD＝1.5b 2.5b＝4b 4b＝3^÷2，b＝9／8 S△ADc＝3x2÷2＝3 S陰影＝（3-9／8）÷2 ＝15／16

粉絲解法12：

也可這樣解： 連結Nc，設S△ANM為a，則 S△NcM＝S△ANM＝a S△ANc＝2a S△ABN：S△ANc ＝BD：Dc＝3：2 S△ABN＝3／2×S△ANc ＝3／2x2a＝3a S△BcM＝S△ABM＝4a S△ABC＝8a 8a＝3x5×1／2＝15／2 a＝15／16

粉絲解法13：

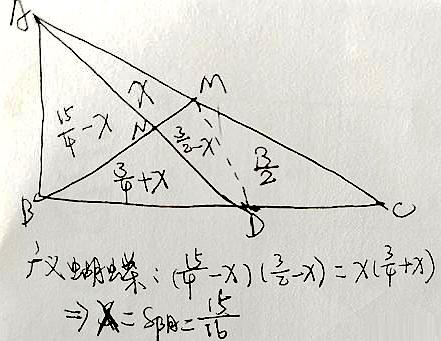
粉絲解法14：

∵連接NC→AM＝MC→S△BAM＝S△BMC＝1／2S△ABC＝15／4→設S△AMN＝a→ S△ANB＝15／4－a→連接MD→S△CMD＝1／2×2／5S△ABC＝1／5×15／2＝3／2→ S△DMC＝S△DMA→S△DMN＝3／2－a→ S△NBD＝15／4－3／2－3／2＋a＝3／4＋a→（15／4－a）／（3／4＋a）＝a／（3／2－a）→a＝15／16。

粉絲解法15：

連接CN。 ∵AM=MC ∴S△ABN=S△CBN S△AMN=S△CMN ∵BD/CD=3/2 ∴S△ABN/S△ACN=3/2 →S△ABN/2S△AMN=3/2 ∴S△ABN=3S△AMN 設S△AMN=1份，則S△ABN=S△CBN=3份，S△CMN=1份，S△ABC=8份 ∴S△AMN=1/8S△ABC=1/8×3×（3 2）÷2=15/16

粉絲解法16：

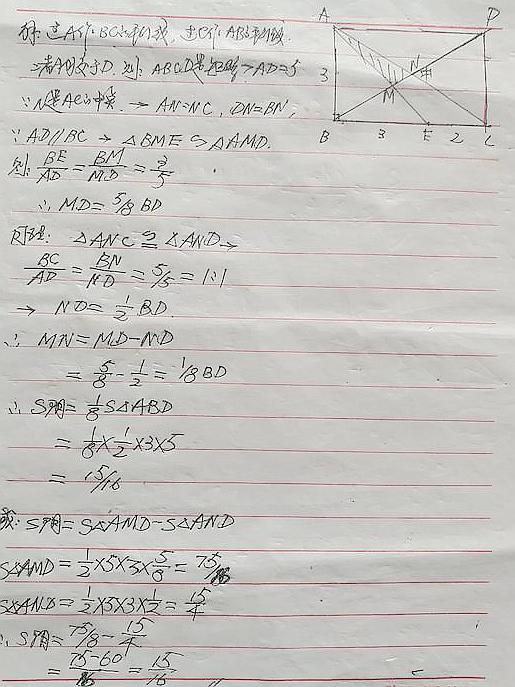
粉絲解法17：

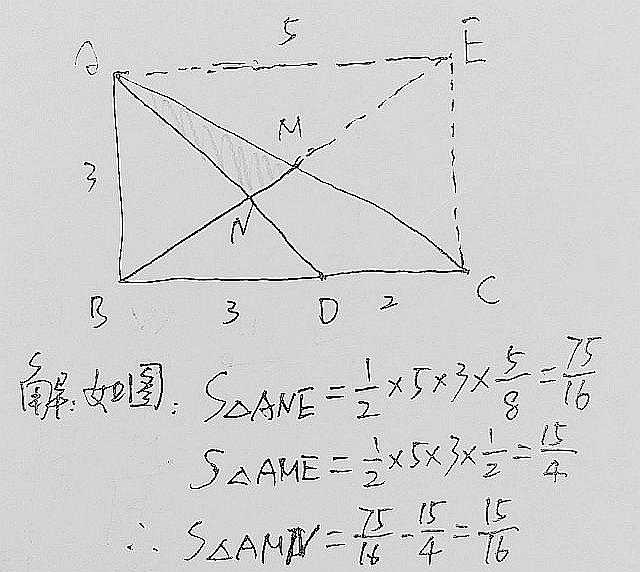
粉絲解法18：

粉絲解法19：

粉絲解法20：

梅氏△MBC與梅氏線AD相交有；(MN/NB)(BD/DC)(CA/CM)∴MN/NB=1/3，S陰=1/4S△ABM=1/8S△ABC=15/16

粉絲解法21：

更多精彩资讯请关注tft每日頭條，我们将持续为您更新最新资讯!