後面準備談談個人對A*算法的理解，這篇算是很重要的基礎知識。

之前說到地圖上一般用網格圖的方式進行簡化和标準化，那麼計算兩點之間的距離，常用的方法有三：

适用于隻可上下左右移動的地圖。最典型的可以看回龍觀地圖：

回龍觀地圖

如上圖，假設你坐一輛出租車，想從A點到B點，隻能向上下左右方向移動，圖中藍線這種斜穿小區的移動是不可以的，所以也叫出租車距離、城市街區距離。

網格圖

如上圖，紅色方塊僅可向上下左右四個綠色方塊移動。

曼哈頓距離就是兩個點在标準坐标系上的絕對軸距總和。

曼哈頓距離

如圖，設A(1,2)，B(4,4)，設直線移動一單位距離為D，則公式為：

(|A.x-B.x| |A.y-B.y|)*D。

可得d=(|1-4| |2-4|)*D=5D。

上圖紅黃綠三條線路的曼哈頓距離都是5D。

适用于可以斜向移動的圖形，如下圖。

網格圖

設直線移動一單位距離為D，那麼斜向移動距離，其實就是根據勾股定理，求腰為D的等腰直角三角形的斜邊，即√2D。

對角線距離

設A(1,2)，B(4,4)，根據公式：

dx=|A.x-B.x|

dy=|A.y-B.y|

D*(dx dy) (√2D-2D)*min(dx,dy)

可得距離約等于3.8D。

因為涉及到開2的平方根計算，必然出現浮點數，計算機處理起來比較耗費資源，在這裡我們可以在損失一定精度的情況下，進行優化。

我們知道√2≈1.4，如果我們假設D=10，則√2D≈14，如此，我們将兩個常數代入公式，就将涉及浮點數的開平方根運算轉換成了整數的加減乘運算。

得出距離為38。

适用于可以随意移動的圖形。

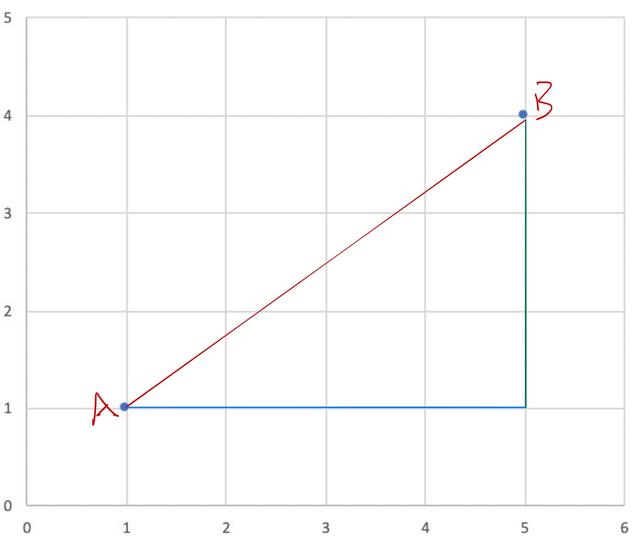
歐幾裡得距離

其實就是根據勾股定理求斜邊。

設直線移動一單位距離為D，公式如下：

dx=|A.x-B.x|

dy=|A.y-B.y|

D*sqrt(dx*dx dy*dy)

如上圖，設A(1,1)，B(5,4)，勾三股四弦五，AB的直線距離必為5。

多啰嗦幾句，因為地球是個球體，我們有山、高原、平原、盆地、海溝等地形，是個三維的，所以求兩個真實地點的距離還要考慮更多的因素，比如兩點的弧長，高度差、地球半徑等。

但是如果隻是估算一個大概的距離，或者隻需要求出兩點的最短路徑，或者兩點就在一個不大的區域内，比如回龍觀。單純地使用歐幾裡得算法也夠用了。

public class Distance { /** * 直線移動一單位距離代價 */ private static final BigDecimal straightCost = new BigDecimal(10); /** * 對角線移動一單位距離代價<br/> * 如果要求高精度，可以設置為BigDecimal(Math.sqrt(2)).multiply(Distance.straightCost); */ private static final BigDecimal diagonalCost = new BigDecimal(14); /** * 曼哈頓距離<br/> * (|start.x-end.x| |start.y-end.y|)*straightCost * * @param start * @param end * @return */ public static BigDecimal manhattan(Node start, Node end) { int dx = Math.abs(start.getX() - end.getX()); int dy = Math.abs(start.getY() - end.getY()); return Distance.straightCost.multiply(new BigDecimal(dx dy)); } /** * 對角線距離<br/> * 曼哈頓距離 (sqrt(2)-2*straightCost)*min(dx,dy) * * @param start * @param end * @return */ public static BigDecimal diagonal(Node start, Node end) { int dx = Math.abs(start.getX() - end.getX()); int dy = Math.abs(start.getY() - end.getY()); BigDecimal dxy = new BigDecimal(dx dy); BigDecimal minDxy = new BigDecimal(Math.min(dx, dy)); BigDecimal result = Distance.straightCost.multiply(dxy).add(Distance.diagonalCost.multiply(minDxy)) .subtract(minDxy.multiply(Distance.straightCost).multiply(new BigDecimal(2))); return result; } /** * 歐幾裡得距離<br/> * 就是根據勾股定理求斜邊。straightCost*sqrt(dx*dx dy*dy) * * @param start * @param end * @return */ public static BigDecimal euclidean(Node start, Node end) { int dx = Math.abs(start.getX() - end.getX()); int dy = Math.abs(start.getY() - end.getY()); return Distance.straightCost.multiply(new BigDecimal(Math.sqrt(dx * dx dy * dy))); } public static void main(String[] args) { Node start = new Node(1, 1); Node end = new Node(5, 4); System.out.println(Distance.manhattan(start, end)); System.out.println(Distance.diagonal(start, end)); System.out.println(Distance.euclidean(start, end)); } }

Node類就x，y兩個參數，不再附上。

更多精彩资讯请关注tft每日頭條，我们将持续为您更新最新资讯!