慣性拉動原理共有3種方式，即離心力型，角動量型，沖量型。其中，離心力型又分為兩種，第一種是擺動型産生離心動力；第二種是轉動型産生離心動力。頭3種，前面已經寫完了，今天，我們就寫轉動型産生離心動力。

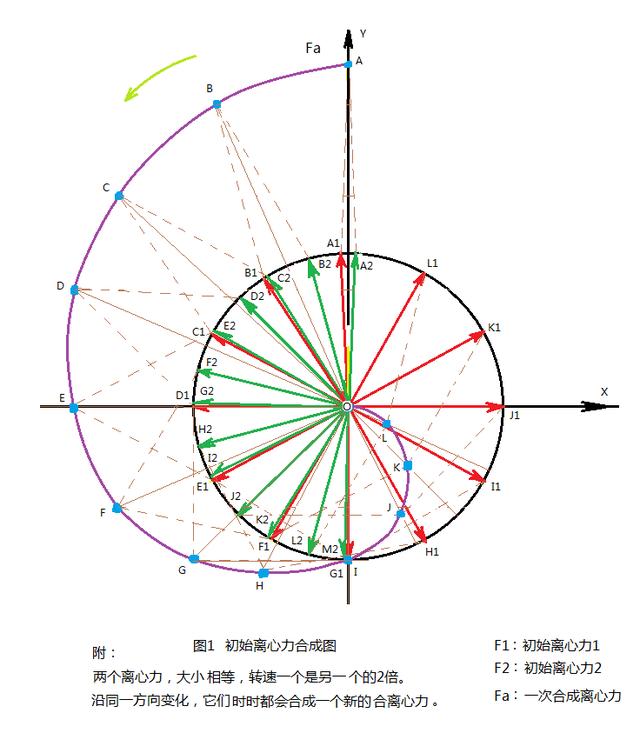
圖1

擺動型産生離心動力，比較明顯，就算是我們平時擺擺手，也能感受到離心力的拉動效果。轉動型産生離心動力，隐藏得比較深，需要比較發達的想象力才會想到。

如圖1所示，坐标系上，兩個原始離心力F1，F2。F1按紅色箭頭逆時針轉動；F2按綠色箭頭逆時針轉動。兩個離心力大小相等，但是F1的轉動速度等于F2的轉速的兩倍，即V1=2V2。 在它們一起轉動的過程中，某一時刻，這兩個力在Y軸上重合，均指向Y軸正方向。這個重合點，就是A1點（紅箭頭标出），和A2點（綠箭頭标出）。

F1運動，變化的軌迹，按A1, B1, C1, D1,.....直到L1，最後回到A1。一個轉動周期結束。F2運動，變化的軌迹，按A2, B2, C2, D2,.......到M2。當F2轉到點M2時，F1已經走完了一個周期，回到A1點上。 在離心力F1,F2轉動的過程中，它們時時都會合成一個新的合離心力Fa。

如圖所示，當F1在A1點時，F2在A2點，它們此時合成離心力為最大值。合離心力Fa =F1 F2 。兩個力在同一條直線上，它們的矢量和，等于它們的代數和。Fa在這裡，就是一次合離心力。此時，它落在點A上。随着時間推移，兩個離心力繼續往前轉動，F1轉到B1時，F2轉到B2，兩個原始離心力之間有一個夾角，它們的合成，将按平行四邊形法則，合成新的合離心力Fa。Fa落在B點上。

就這樣，在後面的時間裡，兩個原始離心力不斷的合成新的合離心力（一次合離心力）。它們分别落在點C,D,E,,,,,直到點L上, 然後，進入到原點O點。我們把這些點連接起來，就會得到如圖1所示的軌迹。這是一個螺旋曲線。它表明合離心力Fa，在轉動的過程中，不斷的減小，縮短，到最後，轉到原點，縮小為0。

經過第一步的合成後，我們就得到了一個螺旋變化的一次合離心力Fa。不過，這個Fa，隻是一次合離心力中的一半。要讓離心力成為動力，我們還要找出另一半Fb。

圖2

如圖2所示，兩個一次合離心力Fa，Fb，在直角坐标系統中，從A（A3）同時出發，一個沿逆時針轉動，變化。另一個沿順時針轉動，變化。Fa轉到B點時，Fb轉到B3點 ,Fa轉到C點時，Fb轉到C3點。一路下來，一路對稱。Fa沿紫色曲線運動，變化，直到點L後，收縮為0，回到原點O點；Fb沒綠色曲線運動，變化，直到L3點後，回到原點，與Fa重合。這兩個一次合成離心力的運動軌迹圖，看起來，就像是一把藤編的扇子。

扇子圖

兩個一次合離心力，相對于Y軸對稱，它們在變化的過程中，必然又要進一步的合成，并且，它們的二次合離心力Fc，必然落在Y軸上。也就是說，這個二次合離心力，已經由在平面上的轉動，進一步收縮為在直線上的平動了（在直線上來回往複振動）。離心力在一條直線上變化了，離心力作為動力也就成為了可能。

今天先寫到這裡，明天繼續寫下半部分。歡迎繼續關注。。

更多精彩资讯请关注tft每日頭條，我们将持续为您更新最新资讯!