在上篇文章中，我向大家展示了為什麼所有的無限循環小數都可以用分數表示，以及如何将無限循環小數轉化為分數。

這篇文章，我們繼續介紹無限不循環小數與無理數之間的關系。

我們知道，無理數都是無限不循環小數，那麼為什麼是這樣呢？

古希臘數學家畢達哥拉斯認為萬物都可以用整數或者整數之比表示。

整數之比按照現在的數學語言，相當于分數。按照畢達哥拉斯的觀點，數隻有整數和整數之比(分數)這兩種。

不過，後來畢達哥拉斯發現了勾股定理，他的這個觀點很快就迎來了質疑。

二、古希臘人眼中的勾股定理

平時我們對勾股定律的描述是，直角三角形直角邊的平方和等于斜邊的平方。不過古希臘人陳述勾股定理用的卻是幾何術語而不是數，描述方式如下：

建立在兩個較小邊上的正方形的面積之和等于建立在最長邊（斜邊，即直角所對的邊）上的正方形的面積。

幾何圖形描述如下：

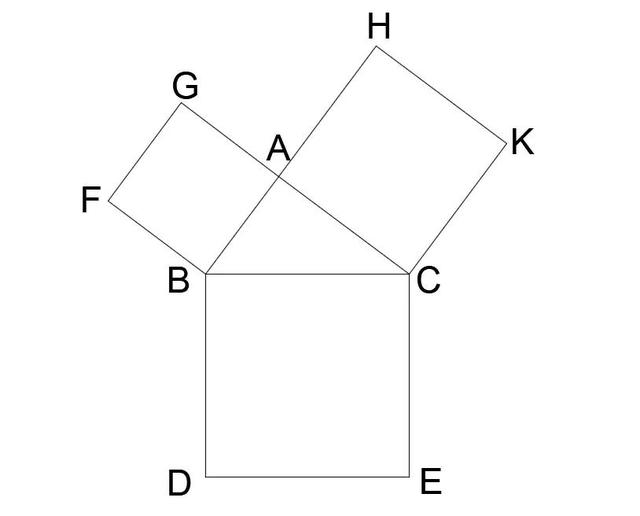
正方形ABFG面積 正方形ACKH面積=正方形BCED面積（AB*AB AC*AC=BC*BC）

雖然勾股定理是畢達哥拉斯發現的，但是他沒有留下勾股定理的證明資料，今天我們能夠看到最早關于勾股定理的證明方法，是歐幾裡得在《幾何原本》“第1卷 平面幾何基礎” 命題47中給予的證明，他是通過在上圖的基礎上添加輔助線來證明的。這裡再多說一句，勾股定理的嚴格證明，其實很難。歐幾裡得為了證明勾股定理，在《幾何原本》中足足引用了3條定義、4條公設、5條公理以及用到提前已經證明好的25個命題的結論，才完成了勾股定理的證明。

三、無理數的發現過程

勾股定理被畢達哥拉斯發現之後，畢達哥拉斯學派成員裡就有人提出了一個問題：

如果有一個邊長是一個單位長的正方形，以及最長邊上面積是這個正方形面積2倍的另一個正方形，那麼另一個正方形的邊與這個正方形的邊的比是多少？

這個時候我們還是引用上面那個圖簡單分析一下這個問題，首先我們先畫出這個問題的圖形出來，如下圖所示：

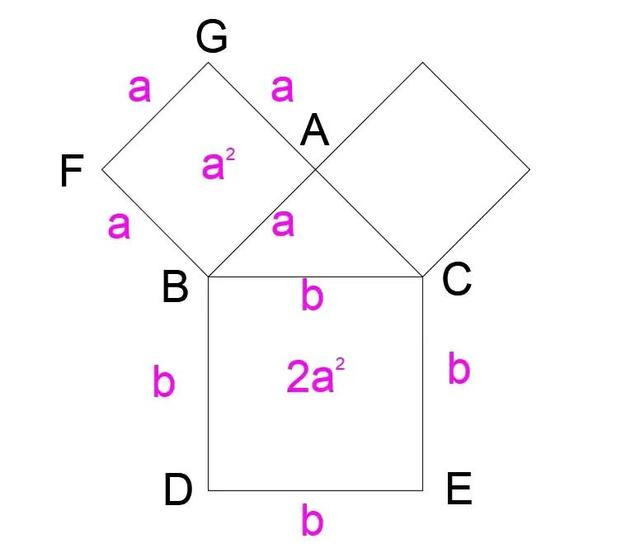
假設正方形ABFG面積為a*a，最長邊上正方形面積為2a*a，那麼BC邊與AB邊長度的比是多少？

我們來分析一下這個問題，畢達哥拉斯不是提出“萬物都可以用整數或者整數之比表示”，首先我們可以很快排除BC邊的長為整數：

如果我們假設a=1，那麼AB=1，BC*BC=2。我們知道，沒有哪個整數的平方是等于2的，因為1*1=1、2*2=4，1和2之間沒有整數，這樣我們就可以排除BC邊的長為整數。

即然BC邊的長不是整數，那按照畢達哥拉斯“萬物都可以用整數或者整數之比表示”的說法，BC邊就隻可能表示為兩個整數的比。

這時候，就有人提出了一個推理過程：

假設BC的長可以表示為2個整數的比，并且這2個整數沒有除了單位1之外的公因子（如果2個整數之間有除了單位1以外的公因子，我們可以約分掉公因子變成最簡形式，也就是2個整數沒有除了單位1之外的公因子），這2個整數我們命名為b和a，且b的平方正好是a的平方的2倍(b*b=2a*a)，這時b就相當于圖上BC邊的長，a就相當于圖上AB邊的長度。

這時我們就能得出一個結論：b*b一定是偶數，且是4的倍數。那麼為什麼呢？下面我們給予證明：

我們已經假設a、b是整數，b*b=2a*a，那麼b*b肯定是偶數。又b*b是兩個相同的整數相乘，且還是偶數，那麼b*b最小數值是4。（整數中最小的數值是1、第二小的是2,而1*1=1是奇數與b*b是偶數不符，2*2=4與b*b是偶數符合，所以b*b的最小數值是4），這時我們就能得出b*b是4的倍數。

這時我們再畫一個圖形，如下圖所示，取BC中點H,以BH為邊作一個正方形BHOI。在這裡我們設BH的長度為c，那麼BC=2BH,也就是b=2c。

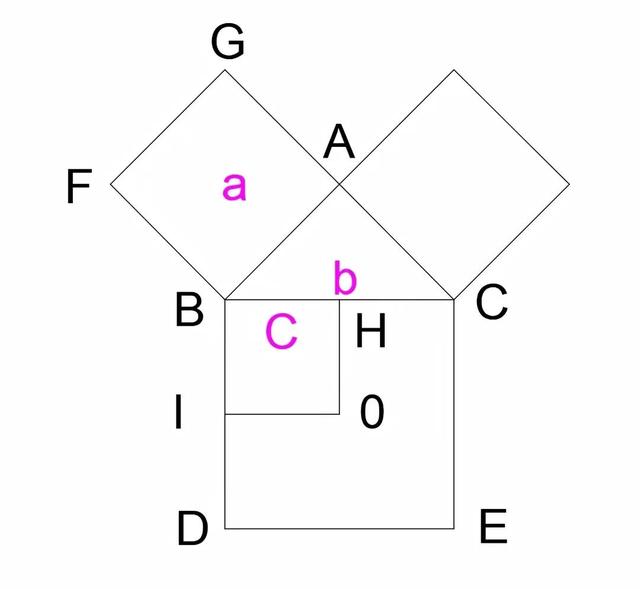
BC邊長=b,BH邊長=c，b=2c

上面我們已經證明了b*b是4的倍數，那麼b肯定是偶數。又b=2c,b是偶數，那麼c肯定是一個整數。

接下來我們繼續

因為b=2c,那麼b*b=2c*2c=4c*c

又因為b*b=2a*a，所以a*a=2c*c

之前我們通過b*b=2a*a證明了b*b的值是4的倍數，同理我們也可以通過a*a=2c*c得出a*a的值也是4的倍數。

接下來就是見證奇迹的時候了：

因為b*b與a*a都是4的倍數，那麼b和a肯定都是偶數，那麼b和a之間肯定有公因子2。

那麼問題就來了，b和a有公因子2，與我們開始的假設＂b與a之間沒有除了1以外的公因子＂矛盾。而b和a之間有公因子2，我們是依據假設和勾股定理推倒出來的。這就隻能說明一個問題，要麼是假設錯了、要麼就是勾股定理是錯的，還有就是假設和勾股定理都是錯的。

既然畢達哥拉斯已經證明了勾股定理是對的，那麼就隻有一種可能，假設錯了，也就是BC邊的長無法用2個整數的比表示。加上之前我們證明了BC邊的長不是整數，這時我們又可以得出結論：畢達哥拉斯有關＂萬物都可以用整數或者整數之比表示＂的結論是錯的。你看，BC的邊長就既不是整數，也不能用整數之比來表示。

類似BC的長度這類無法用整數和整數之比來表示的數，後來人們把這類數稱為＂無理性的數＂，也就是無理數。

我們知道所有的數用小數來區分，隻有兩種:無限循環小數與無限不循環小數。在上篇文章中，我們已經證明了所有的無限循環小數都可以用分數(整數之比)表示，而無理數無法用整數之比(分數)表示，所以無理數隻可能是無限不循環小數。

在上高中的時候，我們都學過等比數列的求和公式：

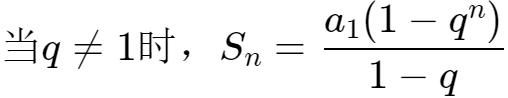
這個公式的推導過程其實很簡單，運用的是錯位相減法;

當q≠1時，

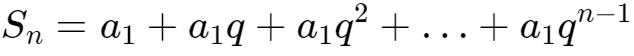
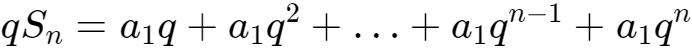
所以，兩式相減，可得：

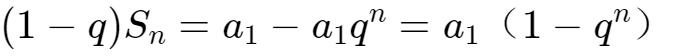
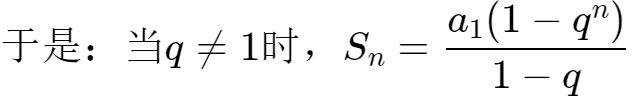
下面我用0.999…與0.67336733…進行舉例:

1、如何将0.999…轉化為分數？

首先0.999…可以看成：

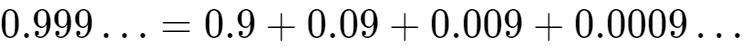
為了用上等比數列的求和公式，我們需要将上述式子向等比數列的表達形式靠齊：

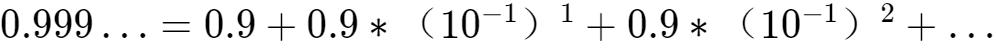
将上述式子和等比數列求和公式進行比較：

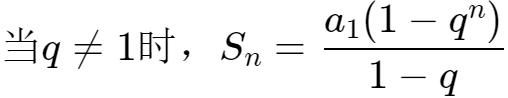
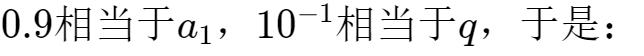
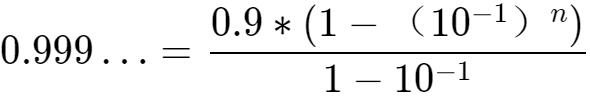
當n趨向于無窮大時，

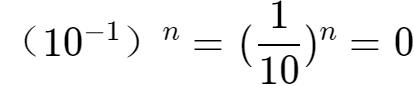
，于是：

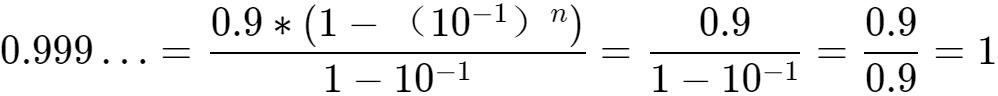
2、如何将0.673367336733…轉化為分數？

其實方法和上面是一樣的，為了用上等比數列的求和公式，可以将0.673367336733…看成：

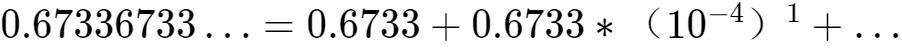
将上述式子和等比數列求和公式進行比較：

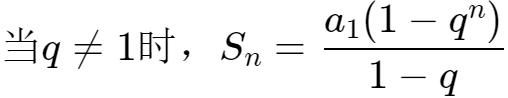
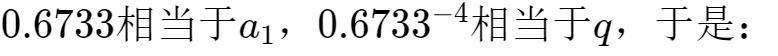
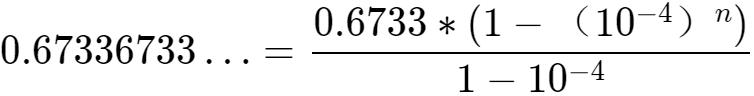
當n趨向于無窮大時，

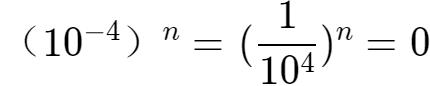
，于是：

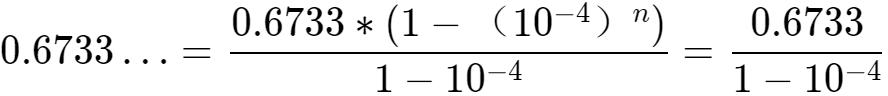
将上述式子繼續簡化，可得：

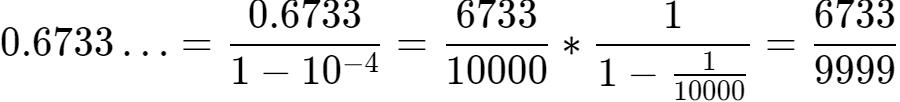
其它的無限循環小數，轉化為分數的過程和上述步驟其實是一樣的，這裡我就不再舉例。

好了，這一講就到這裡了。

我是一個緻力于科普數學、物理的科技媒體。想了解更多相關的知識，歡迎關注我的微信公衆号科學發現之曆程，期待你的到來。

更多精彩资讯请关注tft每日頭條，我们将持续为您更新最新资讯!