易混基礎概念

• 标量：單獨一個數
• 向量：一行/列數
• 矩陣：二維數組
• 張量：一般指多維（0 維張量是标量，1 維張量是向量，2 維張量是矩陣）
• 轉置：沿主對角線折疊

在 Numpy 中定義矩陣的方法，以及進行轉置的方法：

import numpy as np a = np.array([[1, 2, 3], [4, 5, 6]]) a = a.reshape(3, 2) print(a) [[1 2] [3 4] [5 6]] 複制代碼

基本算數關系

與高等數學中矩陣相乘内容一緻：

a = np.array([[1, 2], [3, 4]]) b = np.array([[5, 6], [7, 8]]) print(a * b) print(a.dot(b)) print(np.dot(a, b)) print(np.linalg.inv(a)) # 星(*) [[ 5 12] [21 32]] # 點乘 [[19 22] [43 50]] # 點乘 [[19 22] [43 50]] # 逆運算 [[-2. 1. ] [ 1.5 -0.5]] 複制代碼

範數

範數是一個函數，用于衡量長度大小的一個函數。數學上，範數包括向量範數和矩陣範數。

向量範數

我們先讨論向量的範數。向量是有方向有大小的，這個大小就用範數來表示。

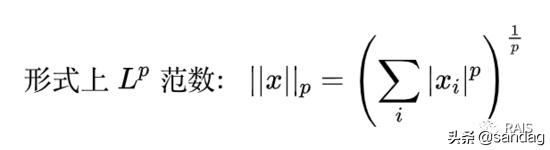
嚴格意義上來說，範數是滿足下列性質的任意函數：

• 當 p=2 時，範數(，可簡化寫成)稱為歐幾裡得範數，可以計算距離。但是我們看到這裡有一個開方運算，因此為了去掉這個開方，我們有可能求的是範數的平方，即範數，這就會減少一次開放運算，在後面提到的損失函數中，範數和平方範數都提供了相同的優化目标，因此平方範數更常用，計算起來也更簡單，可以通過計算，這速度就很快了。
• 當 p=1 時，範數()是向量各元素絕對值之和，在機器學習領域，對于區分 0 和非 0 來說，範數比範數更好用。
• 當 p=0 時，範數實際上不是一個範數，大多數提到範數的地方都會強調說這不是一個真正意義上的範數，用來表示這個向量中有多少個非 0 元素，但是實際上它是非常有用的，在機器學習中的正則化和稀疏編碼中有應用。在一個例子中是這麼說的：判斷用戶名和密碼是否正确，用戶名和密碼是兩個向量，時，則登錄成功，時，用戶名和密碼有一個錯誤，時，用戶名和密碼都錯誤。我們知道有這麼回事，在日後看到相關内容時知道就好了。
• 當 p 為無窮大時，範數也被稱為無窮範數、最大範數。表示向量中元素絕對值中最大的。

矩陣範數

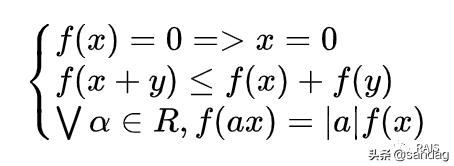
對于矩陣範數，我們隻聊一聊 Frobenius 範數，簡單點說就是矩陣中所有元素的平方和再開方，還有其他的定義方法，如下，其中表示的共轭轉置，tr為迹；表示的奇異值：

奇異值分解

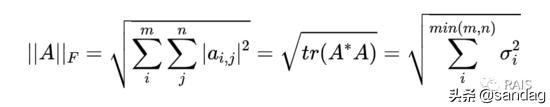
我們熟悉特征分解矩陣中：，奇異分解與之類似：，其中矩陣的行和列的值為、正交矩陣、對角矩陣、正交矩陣，矩陣對角線上的元素稱為的奇異值，其中非零奇異值是或的特征值的平方根；稱為的左奇異向量，是的特征向量；稱為的右奇異向量，是的特征向量。因為奇異矩陣無法求逆，而求逆又是研究矩陣的非常好的方法，因此考慮退而求其次的方法，求僞逆，這是最接近矩陣求逆的，把矩陣化為最舒服的形式去研究其他的性質，僞逆把矩陣化為主對角線上有秩那麼多的非零元素，矩陣中其他的元素都是零，這也是統計學中常用的方法，在機器學習中耶非常好用。

定義

• 對角矩陣：隻有主對角線含有非零元素；
• 單位向量：具有單位範數的向量，；
• 向量正交：如果兩個向量都非零，則夾角 90 度；
• 标準正交：相互正交、範數為 1；
• 正交矩陣：行向量和列向量分别标準正交；
• 特征分解：将矩陣分解為特征向量和特征值；
• 特征值和特征向量：中的和；
• 正定、半正定、負定：特征值都正、非負、都負。

總結

線性代數的一大特點是“一大串”，統一的知識體系，相互之間緊密聯系，非常漂亮，在深度學習中有重要的應用，還是應該要學好。

更多精彩资讯请关注tft每日頭條，我们将持续为您更新最新资讯!