阿基米德折線定理結論-tft每日頭條

阿基米德折線定理結論

生活更新时间:2024-12-19 20:00:56

阿基米德用窮竭法推導出：抛物線下的面積與其外接長方形的面積之比是1:3,今天我們就來讨論X^3曲線下的幾何面積

阿基米德折線定理結論（阿基米德思想的産物）1

前面我們已經讨論了抛物線x^2下的面積，用的不是純代數下的微積分，而是可視化的幾何原理，這種方法是從另一種數學思維出發得到與微積分原理相同的結論。

接着我們讨論X^3下的面積，同樣不是微積分去計算，而是優美的幾何原理。

首先，我們用初等數學可以求出X^3曲線上任意點的斜率，也就是導數，它等于3X^2.

阿基米德折線定理結論（阿基米德思想的産物）2

即：tanθ=3X^2，那麼切線與X軸所圍成的直角三角形的兩條直角邊長就是X^3, X/3。

切線與X軸交點的橫坐标就是X-X/3=2X/3

現在我們做出X^3曲線的所有切線，這就形成了完美的切線區域“切線簇”我們将所有的切線延長至與Y軸相交，以X軸為界 T區域的直角三角形和X軸下方的直角三角形相似，對邊相似比為1:2，面積之比就是1:4

阿基米德折線定理結論（阿基米德思想的産物）3

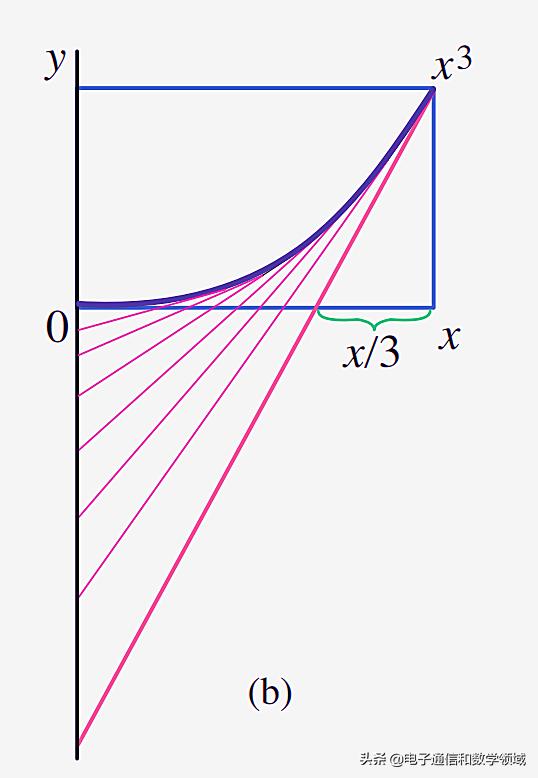
這是一個有趣的結論，為什麼呢？因為X軸上方的切線區域與X軸下方的切線區域面積之比就是1:4(因為對邊之比，也就是所謂的切線之比是1:2)，那麼X軸上方的切線區域與整個切線區域的面積之比就是1:9

由切線區域我們得到一個重要的等式：9S=S 4T,我們得到S=T/2

因為T是直角三角形，所以T的面積等于X/3*X^3*1/2=X^4/6

那麼S的面積就等于:X^4/12=T/2

最終得到X^3曲線下的面積等于S T=X^4/6 X^4/12=X^4/4

這與微積分所得到的結果一緻，

我們還可以得到一個重要的結論：X^3曲線下的面積與其外接長方形的面積之比是1:4

更多精彩资讯请关注tft每日頭條，我们将持续为您更新最新资讯!

查看全部

网友关注

生活智慧阜南怎麼下載
1、自帶軟件商店中下載：桌面找到軟件商店；在軟件商店首頁，可以直接搜索框搜索下載軟件，或者點擊屏幕的... 2023-07-04
生活玉米蒸排骨的家常做法
第一、準備好所有材料排骨一根，帶脆骨的那種、甜玉米一根、姜蒜适量。第二、甜玉米清洗幹淨，對半切開，切成四小塊。第三、姜蒜切小塊，備用。第四、排骨清洗幹淨，瀝幹水分，加入适量的花生油、醬油、蚝油、料酒、鹽，再把姜蒜一起加到碗中，用手把排骨和醬料抓均勻。用筷子攪拌沒有那麼均勻的哦，最好都是用手抓，前提要... 2023-07-04
生活虎頭茉莉和寶珠茉莉有什麼區别
1、葉片。虎頭茉莉和寶珠茉莉，它們的不同首先表現在葉片上面。虎頭茉莉的枝條比較細，葉片是小小的圓圓的，沒有葉尖，一般是單葉對着生長，若是在部分枝幹上葉子長得比較多，可能會出現葉子對生的情況；寶珠茉莉屬于灌木，高的能長到一米左右，枝條雖然也是細細的，但是有棱角，有時候還會有絨毛，全部是單葉對生。葉子一... 2023-07-04
生活綠籮的養殖方法和注意事項
1、光照：綠蘿對光照的要求不高，接受明亮的散射光就可以，不喜歡陽光直接照射。2、溫度：家中的室内溫度... 2023-07-04
生活如何防止鞋子變形
1、正确洗鞋。洗鞋的時候需要把鞋帶取下來，鞋墊最好也拿出來清洗，取出來之後用洗衣液進行清洗，洗衣液柔順清香，不損傷鞋網，表面有污垢的話就用軟刷輕輕地刷洗鞋面。2、晾鞋。晾鞋的時候不要暴曬，防止鞋子變形老化，鞋子的材質都是不經曬，而且不耐高溫，最好在通風幹燥處進行晾曬，讓鞋子自然風幹。3、收鞋。晾曬幹... 2023-07-04
生活印章材質有幾種類型
1、按質地種類分，金屬材料一般用分黃銅印和紫銅印等、不鏽鋼、鋁和為數極少的鉛鋅合金。2、晶質材料制造... 2023-07-04
生活縮小毛衣領的方法
1、首先定好左右兩邊要縫的位置，針線先打好結，針線先從反面穿上來。2、把針往右邊穿上去一小格。3、再... 2023-07-04
生活怎樣設置使得該換燈片換片完成後圖片自...
1、功能區找到[切換]選項卡，點擊打開。找到[換片方式]。2、在左邊幻燈片列表中，選中目标幻燈片。然... 2023-07-04
生活微信朋友圈的3天可見怎麼設置
1、打開手機微信客戶端，在登錄窗口輸入登錄賬号和密碼完成登錄之後，來到微信首頁，點擊底部菜單欄的“我... 2023-07-04
生活做微商的目的是什麼
1、微商的目的是移動終端在網絡新社交媒體平台通過信息傳播達到營銷行為。微商的過程是通過社交媒體找到與自己有着共同的愛好、建立關系的客戶進行銷售産品。微商是現代一種低成本、高性價比的營銷手段，與傳統營銷方式相比，微商”主張通過虛拟”與現實”的互動。2、很多人都認為，微商就是用微信做生意，其實錯了，微商... 2023-07-04
生活欲錢買千裡良駒是什麼生肖
1、欲錢買千裡良駒指的是生肖馬。良駒在這裡指的是馬，所以這裡的“欲錢買千裡良駒”猜字謎謎底就是馬。馬... 2023-07-04
生活炖雞胗的家常做法
第一、雞胗如果買到的是那種凍的，就要事先解凍，我個人建議還是買新鮮的吧，這種口感好味道也好。買回家之後清洗幹淨，上面的那些油脂去掉。第二、鍋裡燒開水之後，把雞胗放進去焯水，雞胗變色之後撈出來。第三、今天告訴大家做的這道炖雞胗不用爆鍋的，直接用電飯鍋或者高壓鍋、電飯煲就可以，鍋子清洗幹淨，放進去小蔥、... 2023-07-04
生活怎麼能快速記身份證号碼
1、首先要知道省份證号碼的構成規律：6位區域号碼+個人的8位出生日期号碼+四位分配順序号碼。2、如果... 2023-07-04
生活昌拓的寓意
昌字本義：善、正當，指正當的言論，還有興盛繁榮之義。用作人名：意指人氣興旺、事業昌達、才能過人。拓一般指開括、開辟、擴充，引申為廣闊、豁達。用作人名意指開明、豁達、謙虛包容之義。姓名：姓名，漢語詞語，意思是由姓和名組成。人的姓一般是自己的部族确定的，名字是人類為區分個體，給每個人特定的名稱符号，是通... 2023-07-04
生活 excel表格裡多個表格如何篩選
1、首先，将要篩選列的字段名稱複制到新的一列的任一單元格，如11150，11081，11094，11... 2023-07-04
生活水下降了怎麼釣魚
1、水庫的水位下降，魚會本能的遊回深水區，因為害怕被擱淺。這種情況下，可以選用抛竿，或者換細長的釣竿... 2023-07-04
生活要釣羅非魚用什麼魚漂
1、在釣羅非魚的時候可以選擇冠作漂、無極漂和阿盧漂，這三種是成功率最高，也是市場上最出名的三種專釣羅非魚的浮漂。2、冠作漂和無極漂的外形極為相似，都屬于長身短粗腳短尾碎的目漂。這樣的外形設計使得冠作漂和無極漂能夠快速翻身下水，而且靈敏度高。冠作漂和無極漂下水後先是快速下沉，快到目标釣目的時候，開始減... 2023-07-04
生活零基礎如何寫代碼
1、配置電腦編程環境：大家準備好電腦之後，為了編程，我們首先要配置好電腦的編譯環境。這樣為我們接下來... 2023-07-04
生活無氰硬金是什麼意思
1、3D硬金是通過電鍍的方式制作而成的黃金飾品，目前行業中分為兩種電鑄，有氰電鑄和無氰電鑄，有氰就是... 2023-07-04
生活廚房防水高度是多少
1、一般來說，廚房防水至少0.3米高，标準是1.3米高。廚房地面需要全部都做防水，牆面也需要返高30... 2023-07-04
生活黃康乃馨花語
1、黃色康乃馨的花語通常有兩種。第一種是對母親懷有感恩之情；第二種是希望友誼深厚、友誼長久的意思。這... 2023-07-04
生活空間簽名在哪裡設置
1、登錄QQ進入QQ空間個人中心。2、點擊導航上面的“空間快捷設置”選擇“空間設置”。3、鼠标移動到... 2023-07-04
生活碘伏棉球怎麼使用
1、以給皮膚消毒為例，首先把碘伏棉球拿出來。2、以消毒的部位為中心，面前按照一個方向旋轉消毒，直徑要達到5厘米以上。3、消毒完就可以扔掉了，因為棉球隻能用一次，不能循環使用，避免造成交叉感染。 2023-07-04
生活肥皂是酸性還是堿性
1、肥皂現在有中性的，也有堿性的和酸性的，一般來說洗衣服的肥皂都是堿性的，堿性的肥皂的去污能力比較強... 2023-07-04
生活拉杆箱怎麼設置密碼
1、将拉杆箱密碼鎖右邊的扣子向右側滑動，将拉杆箱的密碼鎖打開。2、再将拉杆箱密碼鎖下面的滑輪連續滑動... 2023-07-04
生活微信怎麼更換新狀态
1、首先打開微信APP。2、進入微信界面後，點擊右下角的我。3、在【我】的界面點擊你的狀态。4、然後... 2023-07-04
生活購買鍵盤怎麼選擇
1、看手感。大家在選擇機械鍵盤的時候，首先就要用自己的手敲打鍵盤幾聲。因為每個人的性格愛好不同，有些人喜歡彈性軟一些的，而有些人就喜歡彈性大一些的。所以，大家可以在鍵盤上敲打幾聲，就會知道自己喜歡怎樣的鍵盤。2、看按鍵數目。當前市場上最多的還是标準108鍵鍵盤，稍微好一點的鍵盤就會增加一些多媒體功能... 2023-07-04
生活自己如何正确貼手機膜
1、撕下原有手機膜。2、用贈送的擦拭手機的濕布擦拭手機，将手機擦拭幹淨後再用另一外一塊幹布擦幹水分（... 2023-07-04
生活幾月扡插金銀花
1、金銀花在7～8月間插扡。2、插扡一般在雨季進行。在夏秋陰雨天氣，選健壯無病蟲害的1～2年生枝條，... 2023-07-04
生活買洗衣機怎麼挑選
1、根據所處環境不同選：日常在辦公室不怎麼出汗，衣物一般也就染個灰塵什麼的，建議選滾筒洗衣機。日常工作環境易出汗，衣物也很容易染上髒污，建議波輪洗衣機。2、根據擺放空間選：家中空間充裕，考慮整體設計，選擇可以嵌入的滾筒洗衣機。家用空間局促，沒有合适的位置放洗衣機，選擇容易移動的波輪洗衣機，臨時調整位... 2023-07-04

tft每日頭條

> 生活

> 阿基米德折線定理結論

阿基米德折線定理結論

相关生活资讯推荐

热门生活资讯推荐

网友关注