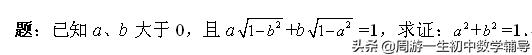
題：已知a、b大于0，且a√(1-b2) b√(1-a2)=1，求證：a2 b2=1．

這是一道經典代數證明題，對于初中生來說，最容易想到的方法是将已知等式變形——去根号，從而可得如下證法：

證法1：由已知，得：a√(1-b2)=1-b√(1-a2)，

兩邊平方，得：a2(1-b2)=1-2 b√(1-a2)b√(1-a2) b2 (1-a2)，

整理，得2b√(1-a2)=1-a2 b2，

兩邊再平方，得：4b2 (1-a2)=1 a4 b4-2a2 2b2-2a2b2，

移項、合并同類項，整理，得

a4 b4 2a2b2-2a2-2b2 1=0，

即(a4 b4 2a2b2)-2(a2 b2) 1=0，

所以(a2 b2)2-(a2 b2) 1=0，

因式分解，得(a2 b2-1)2=0，

所以a2 b2-1=0，a2 b2=1．

點評：去根号是解決無理式問題最常用的基本方法，這種證法雖然顯得有點笨拙，但笨中有巧，考驗的是大家對算式的運算能力和變形能力．

如果由已知及求證式子想到完全平方公式(x-y)2=x2 y2-2xy，并變形為xy=[( x2 y2)-(x-y)2]/2，則可以直接把已知等式中的a√(1-b2)和b√(1-a2)分别進行轉化，得到如下證法：

證法2：由完全平方公式，得

a√(1-b2)={a2 [√(1-b2)]2-[a-√(1-b2)]2}/2

={a2 1-b2-[a-a√(1-b2)]2}/2，

同理，b√(1-a2)= {b2 1-a2-[b-√(1-a2)]2}/2，

兩式相加，并整理，得

a√(1-b2) b√(1-a2)

=1-{[a-√(1-b2)]2 [b-√(1-a2)]2}

因為a√(1-b2) b√(1-a2)=1，

所以1=1-{[a-√(1-b2)]2 [b-√(1-a2)]2}，

整理，得[a-√(1-b2)]2 [b-√(1-a2)]2=0，

因為[a-√(1-b2)]2和[b-√(1-a2)]2都是非負數，

所以[a-√(1-b2)]2=0且[b-√(1-a2)]2=0，

所以a=√(1-b2)，b=√(1-a2)，

兩邊平方，并整理，均可得：a2 b2=1．

點評：完全平方公式不僅是多項式相乘運算的工具，它的變形在解決平方問題中的作用更加重要．

如果從求證的結論入手，既然a2 b2=1可以成立，則1- a2=b2，1-b2=a2，于是已知等式中的a與√(1-b2)，b與√(1-a2)就必須是分别相等的，即a-√(1-b2)=0，b-√(1-a2)=0，因此，可考慮構造[a-√(1-b2)]2 [b-√(1-a2)]2，然後證明[a-√(1-b2)]2 [b-√(1-a2)]2=0．

證法3：設s=[a-√(1-b2)]2 [b-√(1-a2)]2，則

s=a2-2 a√(1-b2) 1-b2 b2-2 b√(1-a2) 1-a2

=2-2[a√(1-b2) b√(1-a2)]，

因為a√(1-b2) b√(1-a2)=1，

所以s=2-2×1=0，

即[a-√(1-b2)]2 [b-√(1-a2)]2=0，

所以a-√(1-b2)=0，b-√(1-a2)=0，

所以a=√(1-b2),b=√(1-a2)，

兩邊平方，整理，得a2 b2=1．

點評：構造法是數學解題的重要方法之一，根據問題特征及其解題需要構造相關的式子往往是問題解決的關鍵．

如果把a2 b2作為整體，設為s，讓s參與到已知等式的變形中去，則可得如下證法．

證法4：設s= a2 b2，則

把已知等式兩邊直接平方，得

a2(1-b2) b2(1-a2) 2ab√[1-( a2 b2) a2b2] =1，

整理，得：a2 b2-2 a2b2 2ab√[1-( a2 b2) a2b2]=1，

所以s 2 a2b2 2ab√(1-s a2b2) =1，

移項，得2ab√(1-s a2b2)=1 –s 2 a2b2，

兩邊再平方，得

4 a2b2 (1-s a2b2)=1 s2 4a4b4-2s 4 a2b2-4 a2b2s，

即4 a2b2 -4a2b2s 4a4b4)=1 s2 4a4b4-2s 4 a2b2-4 a2b2s，

移項、合并同類項，得s2-2s 1=0，

所以(s-1)2=0，s=1，

所以a2 b2=1.

點評：整體思想是數學的重要思想，從整體出發，進行整體處理可以大大簡化算式的變形與化簡．

如果從已知等式結構想到勾股定理及托勒密定理——圓内接四邊形兩組對邊的乘積之和等于對角線的乘積．此時可以得到如下比較簡單的證法：

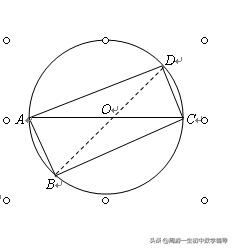
證法5：如圖，構造直徑為1的圓O．在⊙O上取點A，作直徑AC，作弦AB=a，AD=b，連接BC、CD．

因為AC為直徑，所以AC=1，且∠ABC=∠ADC=90°，

所以BC=√(1-a2)，CD=√(1-b2)，

連接BD，則由托勒密定理，得

AB·CD AD·BC=AC·BD，

即a√(1-b2) b√(1-a2)=BD，

因為a√(1-b2) b√(1-a2)=1，

所以BD=1，所以BD是⊙O 的直徑，

所以∠BAD=90°，

所以AB2 AD2=BD2，

所以a2 b2=1．

點評：聯想是數學學習的基本素養，是打開解題思路的鑰匙，由此及彼進行聯想，将問題轉化為相關的問題．

如果從已知等式中的被開方數1-a2≥0，1-b2≥0，得a2≤1，b2≤1，聯想到三角函數的正、餘弦，利用三角函數代換可得如下證法．

證法6：設a=sinα，b=sinβ（0°≤α、β≤90°），則已知等式可化為：

sinα√[(1-(sinβ)2] sinβ√[(1-(sinα)2]=1，

即sinα√(cosβ)2 sinβ√(cosα)2=1，

因為0°≤α、β≤90°，所以0≤cosα、cosβ≤1，

所以sinα·cosβ sinβ·cosα=1，

所以sin（α β）=1，

所以α β=90°，

所以sinβ=cosα,

所以a2 b2=(sinα)2 (cosα)2=1．

點評：在數學解題中進行一題多解訓練，有利于發散思維的培養，解題思路的開拓和解題能力的提高，從而誘發創新思維．

更多精彩资讯请关注tft每日頭條，我们将持续为您更新最新资讯!