指數函數基礎題-tft每日頭條

指數函數基礎題

生活更新时间:2024-12-02 20:20:40

指數函數的重要的初等函數之一，是中學函數的基本知識。教師教育網根據考試大綱整理了相關知識，如下。

一、指數函數的概念

函數y=ax(a>0且a≠1)叫做指數函數，其中x是自變量，a為常數，函數定義域為R。

二、指數函數的圖象和性質

指數函數y=ax（a＞0，且a≠1）的圖象和性質：

1.當0<a<1時，圖像如下：

指數函數基礎題（高頻考點指數函數）1

定義域：R

值域：（0， ∞）

恒過定點：圖像恒過定點（0,1），即當x等于0時，y=1

單調性：在（-∞， ∞）上是減函數

函數值的變化規律：

（1）當x<0時，y>1

（2）當x=0時，y=1

（3）當x>0時，0<y<1

2.當a>1時，圖像如下：

指數函數基礎題（高頻考點指數函數）2

定義域：R

值域：（0， ∞）

恒過定點：圖像恒過定點（0,1），即當x等于0時，y=1

單調性：在（-∞， ∞）上是增函數

函數值的變化規律：

（1）當x<0時，0<y<1

（2）當x=0時，y=1

（3）當x>0時，y>1

三、底數對指數函數的影響

1.在同一坐标系内分别作函數的圖象，易看出：當a>l時，底數越大，函數圖象在第一象限越靠近y軸；同樣地，當0<a<l時，底數越小，函數圖象在第一象限越靠近x軸。

2.底數對函數值的影響如圖：

指數函數基礎題（高頻考點指數函數）3

③當a>0，且a≠l時，函數

指數函數基礎題（高頻考點指數函數）4

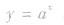
與函數y=

指數函數基礎題（高頻考點指數函數）5

的圖像關于y軸對稱。

四、指數函數圖象的應用

函數的圖象是直觀地表示函數的一種方法，函數的很多性質，可以從圖象上一覽無餘。數形結合就是幾何與代數方法緊密結合的一種數學思想，指數函數的圖象通過平移、翻轉等便可得出一般函數的圖象，利用指數函數的圖象，可解決與指數函數有關的比較大小、研究單調性、方程解的個數、求值域或最值等問題。

指數函數的知識有其抽象性，記憶需要把握其規律性，可以從函數圖像的規律中進行記憶。考生還可結合函數的知識總結的相關知識進行複習。

更多精彩资讯请关注tft每日頭條，我们将持续为您更新最新资讯!

查看全部

网友关注

生活隔水炖湯一般炖多久
1、１－２小時。2、隔水炖湯的時間并非越長越好，一般是用大火燒開，然後用文火炖１－２小時即可，如果時... 2023-07-12
生活手機優化開不了機怎麼回事
1、可能是系統不匹配問題。2、同時按住音量下鍵+電源鍵15秒重啟手機。3、使用充電器為手機充電30分... 2023-07-12
生活一分鐘教你做一個可以拉伸的心形小紙條
第一、先将小紙條對折，然後打開，然後左邊在1/4處折疊，左邊再次折疊，右邊也是在1/4處折疊，右邊再次折疊，折疊好之後，打開，形成八等分。第二、然後從紙條的左邊開始折疊到右邊的1/4處，打開，從左邊數第三份對折，同樣道理，從紙條的右邊開始折疊到左邊的1/4處，打開，從右邊數第三份對折。第三、把紙條反... 2023-07-12
生活正宗四川泡辣椒方法是什麼
1、準備好食材：花椒适量，幹辣椒适量，山奈适量，冰糖适量，白酒适量，清水适量，泡菜鹽适量，八角适量，2、在一個幹淨無油的鍋内加入準備做泡菜水的清水和鹽，加熱使鹽溶化，然後晾涼，将冷卻的鹽水倒入泡菜壇子中，水的量應該在泡菜壇子的2/3處。3、加入适量的大料（八角）、山奈、花椒、幹辣椒、冰糖、白酒，加入... 2023-07-12
生活學芭蕾舞最晚年齡是幾歲
1、芭蕾從來沒有學的早晚的問題，芭蕾動作基礎全部在于肌肉運用身體協調性以及韌帶柔韌性這三塊，具體指小腿腹部肌肉量，能否自由控制身體關節，以及身體柔韌性最具體的是劈叉)。2、但是想練成專業水平基本上可能不大，畢竟芭蕾對于軟開度要求很高，沒有基礎的情況下無論18還是20歲都再很難達到芭蕾所需的最基本軟度... 2023-07-12
生活立夏的含義和諺語
1、立夏，是二十四節氣中的第7個節氣，夏季的第一個節氣，交節時間在每年公曆5月05－07日。此時北鬥... 2023-07-12
生活小葉紫檀手磨和機磨有什麼區别
1、機器打磨大多使用磨盤，将粗加工後的一批珠子一起放入磨盤内，蓋好蓋子，開動機器高速旋轉，珠子們在磨盤裡滾動摩擦，達到快速批量打磨抛光的目的。手工打磨則是人工逐個打磨，将珠子卡在轉軸上，依次使用目數由低到高的砂紙及棉布打磨抛光，由于是人工一個一個打磨，所以加工速度比較慢，人工成本較高。2、機器打磨速... 2023-07-12
生活羅漢肉在豬的身上哪個部位
豬肝的邊沿部分。羅漢肉就是豬肝沿，豬肝沿是豬肝的邊沿部分，即豬胸腔和腹腔之間的一片平滑肌，分隔兩腔固定内髒器官，起保護作用，整片未切割前呈圓形。由于靠近肝髒部位，遂稱豬肝沿。因有運動，肉質細嫩；同時夾雜筋膜，有韌性，耐嚼。如何挑選豬肉：1、觸摸不黏手。觸摸新鮮的豬肉表面，感覺微幹或稍濕，但不黏手；而不新鮮的豬肉，摸起來會感覺表面幹燥或有些黏手。2、按壓有彈性。新鮮豬肉質地緊密且富有彈性，用手指按壓 2023-07-12
生活芹菜雞肉餡餃子怎麼做
1、準備好用料：青菜一把，胡蘿蔔一個，雞胸肉一塊，餃子皮适量，輔料西紅柿一個。2、芹菜一把，洗幹淨後将葉片去掉。燒開一鍋水，加入适量鹽和幾滴油，将芹菜放入鍋中汆燙至變色。撈出來，放入冷水中投涼，防止顔色變黃。3、将處理好的芹菜切成末，胡蘿蔔切末，雞胸肉剁成泥，一起放入盆中。4、先在胡蘿蔔和芹菜碎上淋... 2023-07-12
生活可愛的七星瓢蟲折法詳細圖解
第一、準備一張正方形紙和一支黑筆。第二、先把正方形紙的角和角對折起來。第三、再把兩側的角往下折，不要并齊，要露出下層中間的部分，兩邊的角當作瓢蟲的翅膀。第四、把紙反過來，把上面的角往下折一段。第五、再把折下來的小角往回折一小段。第六、把紙反過來，上面露出來的小尖當作瓢蟲的頭。第七、用黑筆在兩個翅膀上... 2023-07-12
生活幼兒園手工折紙——蘑菇
第一、準備一張正方形的彩紙和一支彩筆。第二、将正方形的彩紙角與角對折，再打開，得到中間的兩條對角線。第三、把三個角往中心折，壓平，下面那個角不動。第四、把上面的邊以中心點為對稱軸往下折。第五、把彩紙反過來，按平。第六、把上面的兩個角往中心線上折。第七、上層的紙不動，把中間的紙從裡面往中心線上折。第八... 2023-07-12
生活大白菜都長什麼蟲
1、菜青蟲、棉鈴蟲：幼蟲以食葉為主，啃食葉肉，留下一層透明的表皮；3齡後可蠶食整個葉片，蟲口累累，重則僅剩葉脈，影響生長發育和包心，造成減産，降低商品價值，還可導緻軟腐病。藥劑可用0.5%苦參堿，對防治菜蚜、菜青蟲、棉鈴蟲、紅蜘蛛等蔬菜害蟲有很好的效果。2、菜蚜：在葉背刺吸植物汁液，造成植株生長不良... 2023-07-12
生活曬臘肉怎麼腌制
1、買回長條的五花肉或三層肉，不用洗，抹上鹽腌制七到八小時。2、用涼開水洗淨，将肉的一頭穿上繩。這個過程有點難度，可以用刀先切開個小口，後用螺絲刀穿洞，穿上繩子，我用的是鈎針，直接就把繩拉進洞裡了。3、挂上瀝幹水份。4、将醬油，料酒，大蒜調配好也可以依個人口味加入花椒，辣椒等)，倒入瀝幹水的肉中。5... 2023-07-12
生活金苞花怎麼修剪
1、修剪時間。金苞花最佳修剪時間是在春季好秋季，春季時期萌發新芽和長葉的時機，這時應該及時将一些弱枝、舊葉修剪掉。而秋季正值它的開花季節，當花期過後應該及時将殘花修剪，避免不必要的養分消耗。冬季一般無需修剪，但是有黃葉存在的話，還是需要及時修剪掉的，以免掉入盆内，避免病害發生。2、修剪方法。在金苞花... 2023-07-12
生活怎樣看微信别人撤回的照片
1、有時候收到的圖片會被發送者撤回，這個時候就很想知道到底發送的是什麼内容；2、打開手機的文件夾管理，點擊所有文件；3、打開騰訊文件夾，找到文件名開頭是Mic的文件夾；4、根據時間排列找到時間最接近現在的那個文件夾點進去，找到名字是image2的文件夾點進去；5、找到名字是9a”，6d”等名字比較奇... 2023-07-12
生活食鹽可以去角質嗎
1、臉上角質層過厚是可以用食鹽磨掉的，但在摩擦的過程中會對皮膚造成一定的物理損傷。所以一定要注意方法，并控制好力度，否則得不償失。2、此外，食鹽的刺激性較強，皮膚本身有破損，或者角質較薄，皮膚較為敏感的人不要用食鹽去角質。3、為了避免食鹽顆粒表面過于粗糙，損傷皮膚，可以采取下面方法：取一啤酒瓶蓋食鹽... 2023-07-12
生活一般給草莓施什麼肥最好
1、草莓生長初期吸肥量很少，自開花以後吸肥量逐漸增多，随着果實不斷采摘，吸肥量也随之增多，特别是對鉀和氮的吸收量最多。定植後吸收鉀量最多，其次是氮、鈣、磷、鎂、硼。鉀和氮的吸收随着生育期的進展而逐漸增加，采摘開始時，養分需要量急劇增加，磷和鎂呈直線緩慢吸收。缺磷時草莓枯葉較多，新生葉形成慢，産量低，... 2023-07-12
生活香格裡拉在哪
1、香格裡拉位于雲南省迪慶藏族自治州香格裡拉縣青藏高原南緣，橫斷山脈腹地，是滇、川、藏三省區交彙處。... 2023-07-12
生活打籃球如何練習投三分球
1、投籃姿勢。标準的姿勢當然大有好處，但是如果你已經有了自己習慣的穩定姿勢，并且在中距離準心不錯，不妨就用自己習慣的投籃姿勢，這樣可以讓你的力量提升較快。2、善用腿部力量。單純用臂力進行遠投是很難的。投籃時微微下沉膝蓋，腳步蹬地，借由來自地面的力量，輕輕擡升身體，并順勢出手将球投出。3、提高投籃弧線... 2023-07-12
生活錦帶花怎麼種植
1、選擇花盆：種植錦帶花我們最可以用透氣的素陶盆，因為這個類型的盆排水透氣的效果相對比其他的花盆好一點，不過其他的花盆也是可以的，隻要不是塑料盆都行。2、土壤：想要種植一盆好的植物，土壤選擇是重要的一步，一般我們都會選擇土質比較疏松的肥沃的沙質土壤，沙質土壤的排水性能是最好的，而且它的透氣也比較好，這樣的土壤能給錦帶花帶來更多營養。3、澆水：在錦帶花的這個生長過程中，水分控制的好事最重要的，在春天 2023-07-12
生活女生怎麼和男生聊天
1、尋找兩個人的共通點。共通點，意思是你們彼此有所交集的，有相似性的點。對方是自己喜歡的人，誰都不想說錯話。這個時候，和男生聊天技巧可以找兩個人之間的共通點。2、聊對方想說的。看到這個，有人會問：我怎麼會知道他想說什麼？我要知道我就不擔心聊天了。所以這一步的聊天技巧之前，我們要先知道對方想說什麼。可... 2023-07-12
生活烤箱預熱是指怎樣預熱
1、插上電烤箱電源。2、打開電烤箱開關控制器。3、查看控溫燈是否亮起，亮起表示電源已經接通并開始加熱。4、等待十分鐘左右。5、查看電源燈是否熄滅，熄滅表示已經達到想要控制的溫度。6、放入要烘烤的食品。 2023-07-12
生活發橫财最靈的方法
1、佩戴貔貅貔貅是我國自古以來一直十分受人敬仰的神獸，他的獨到之處在于，可以幫助世人得到更多的财富。... 2023-07-12
生活繡球花移栽的最佳時間是什麼時候
1、最合适的季節是春季和秋季，春天移栽最好是趁着還沒有開花去進行移栽，如果開花了建議不要去嘗試進行移栽，這時候還是靜靜的觀賞花卉比較重要，等到花開完進入秋季落葉之前也是可以進行移栽的，隻要保證在這期間進行移栽，不管是對于恢複還是生長都是特别有利的。2、移栽之前我們需要給它進行修剪，像一些不健康的枝條... 2023-07-12
生活蒸餃怎麼包
1、首先我們把餃子皮擀好，捏成這種形狀，然後從底部開始，一點點的往前捏，步伐”均勻一緻，心态要放好，千萬不能着急，尤其是剛開始學包餃子的新手。2、其二，要特别注意的地方是，包餃子的時候，如果感覺餃子皮不黏，可以蘸點清水上去，這樣黏合起來就容易多啦！ 2023-07-12
生活用輸液管怎麼編挂件
第一、輸液管拆開，留下輸液管的零部件。第二、輸液管拆開，留下輸液管的零部件，把輸液管剪成3-4根，對半折第三、然後用帶圈的零部件固定到，用剪刀剪細輸液管第四、再剪一些小的輸液管，用來裝飾，放在已固定好的輸液管上，圖案可以自己想像第五、還可以裝上一些金屬扣，放在自己喜歡的物件上面裝飾，很好看第六、還可... 2023-07-12
生活異地學駕照需要哪些條件
1、報考駕駛證是有戶籍限制的。根據規定，異地憑1年以上的暫住證可以考C1以下的駕駛證。B2以上的駕駛證必須在戶籍所在地考試。2、異地考取的駕駛證隻能在異地發證的交管部門換證C1以下駕駛證不需要年審，六年換證就可以了)。3、如果你在異地取得C1以下駕駛證後，可以将駕駛證轉到你戶籍所在地的交管部門，轉證... 2023-07-12
生活牆紙怎麼清潔
1、色筆污漬的清潔。如果壁紙上不慎有色筆的污漬，特别是家裡面有小孩的朋友。可以選擇用橡皮、肥皂水等清除上的污迹。一般鉛筆漬就用橡皮輕輕擦拭表面；如果是水彩筆漬則可用肥皂水擦拭，然後用柔軟的幹布擦看景；如果是蠟筆漬則用海綿輕輕擦幹淨；圓珠筆漬需要用半濕毛巾來清潔。2、表面灰塵處理。對于壁紙表面的灰塵，... 2023-07-12
生活山藥怎樣曬幹
1、用清水将山藥清洗幹淨。2、削去山藥的外皮。3、用刀将山藥切成片。4、将山藥片放入90度溫水中浸泡半個小時（目的是将山藥的粘液浸泡出來）。5、接着将山藥片擺放在案闆上曬制。6、曬制2~3天，幹山藥已經曬制完成。 2023-07-12
生活沉香怎麼區分真假
1、看沉香紋路是否清晰，色澤是否雷同，如果是，那麼沉香便是假的。2、用手揉擦沉香表面，如果表面有油膩... 2023-07-12

tft每日頭條

> 生活

> 指數函數基礎題

指數函數基礎題

相关生活资讯推荐

热门生活资讯推荐

网友关注