我們的數學課本給出了常用函數求導的數學過程和結果,但其過程包含的優美的數學規律卻很少體現,本篇我們就以指數函數為例來發現數學的美
如下是一個有關2為底的指數函數:2^t,我們在這裡研究下它的導數所蘊含的數學規律
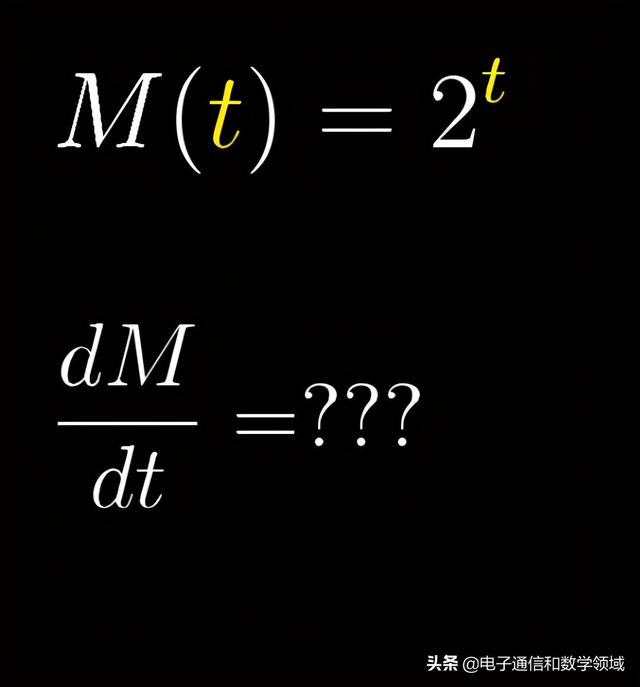
根據函數的求導原理,2^t的導數的表達式就是

以及2^t導數所表示的切線斜率就是
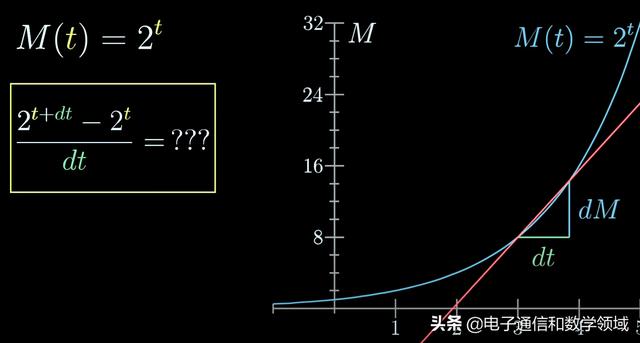
我們将2^(t dt)進行整合,如下圖可以分拆為2^t 和2^dt
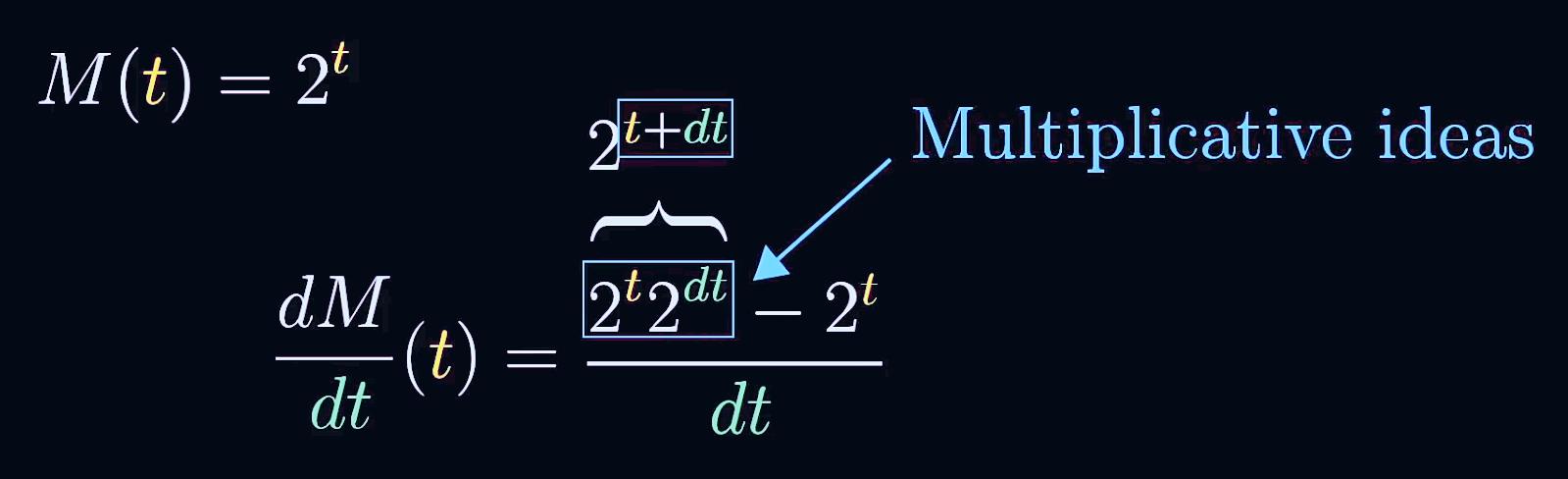
我們将2^t提取出來,如下圖,我們現在要解決的就是等式右邊括号内的式子

這是本篇的重點,我們假設dt=0.001,那麼其結果等于
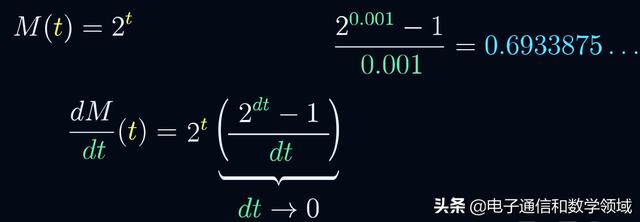
我們将上述dt繼續縮小100倍,其結果仍是0.693……那麼這個值是不是一個常數呢?
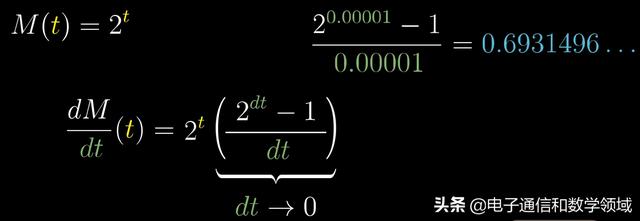
為了驗證我們的猜測,我們繼續将上述dt縮小1000倍,結果仍然是0.693……隻是不斷地趨于一個常數
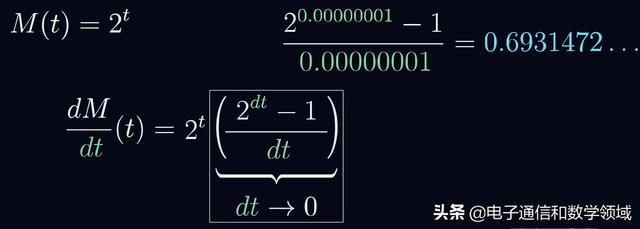
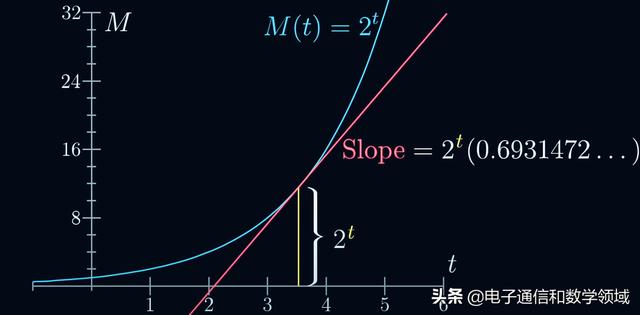
所以我們可以肯定2^t的導數就是2^t乘以一個常數,這是所有指數函數都有的特性
更多精彩资讯请关注tft每日頭條,我们将持续为您更新最新资讯!




