數姐有話

今天數姐給大家帶來的是初二下冊去年的期中考試題，注意考察了一元二次方程，勾股定理，平行四邊形等章節内容。本卷考察不難，但同學們要注意的是，中考時，這三章内容都比較重要，适合出中等偏難的試題。

一、精心選一選（每小題3分，共24分）

1．已知x=2是一元二次方程x2 mx﹣8=0的一個解，則m的值是（　　）

A．2 B．﹣2

C．﹣4 D．2或﹣4

2．将方程x2 4x 2=0配方後，原方程變形為（　　）

A．（x 4）2=2 B．（x 2）2=2 C．（x 4）2=﹣3 D．（x 2）2=﹣5

3．直角三角形兩邊長分别是3、4，第三邊是（　　）

A．5 B．

C．5或

D．無法确定

4．四邊形ABCD的對角線AC、BD互相平分，要使它成為矩形，需要添加的條件是（　　）

6．若關于x的方程（m﹣2）x2﹣2x 1=0有兩個不等的實根，則m的取值範圍是（　　）

A．m＜3 B．m≤3

C．m＜3且m≠2 D．m≤3且m≠2

7．如圖，已知四邊形ABCD中，R，P分别是BC，CD上的點，E，F分别是AP，RP的中點，當點P在CD上從C向D移動而點R不動時，那麼下列結論成立的是（　　）

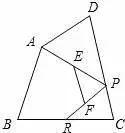
A．線段EF的長逐漸增大

B．線段EF的長逐漸減少

C．線段EF的長不變

D．線段EF的長與點P的位置有關

8．如圖，以Rt△ABC的斜邊BC為一邊在△ABC的同側作正方形BCEF，對角線交于點O，連結AO，如果AB=4，AO=4

，那麼AC的長等于（　　）

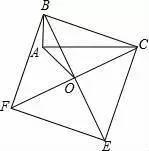
A．12 B．16

C．4

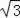
D．8

二、細心填一填（每空2分，共24分）

9．方程x2=2x的解是．

10．如圖，等邊△BCP在正方形ABCD内，則∠APD=度。

11．矩形的兩條對角線所夾的銳角為60°，較短的邊長為12，則對角線長為．

12．若關于x的方程x2﹣2x﹣m=0有一個實數根為x=3，則方程的另一個根為；m的值為．

13．菱形ABCD中，對角線AC、BD交于點O，若AC=6cm，BD=8cm，則菱形ABCD的周長為cm，面積為cm2．

14．如圖，正方形網格的邊長為1，點A，B，C在網格的格點上，點P為BC的中點，則AP=．

15．如圖，已知正方形ABCD的邊長為

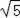
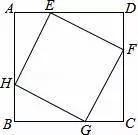
，點E，F，G，H分别在正方形的四條邊上，且AE=DF=CG=BH，則四邊形EFGH的形狀為_______，它的面積的最小值為_______．

16．如圖，AD∥BC，AB⊥BC，動點E從點A開始沿AD運動，動點F從點B開始沿BC運動，AM=10cm，BN=8cm

（1）若動點E的速度為2cm/s，動點F的速度為1cm/s時，當運動時間為秒時，以E，F，N，M為頂點的四邊形為平行四邊形；

（2）若AB=4cm，當點E、F的運動速度比

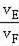
=時，在某一時刻，四邊形EMFN為菱形.

三、作圖題（3分）

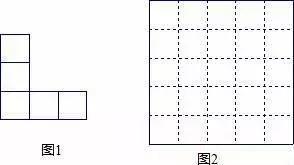
17．現有5個邊長為1的正方形，排列形式如圖1，請在圖1中用分割線把它們分割後标上序号，重新在圖2中拼接成一個正方形．（标上相應的序号）

四、耐心算一算（每小題4分，共16分）

18．用配方法解方程：2x2 2x﹣1=0．

19．用适當的方法解關于x的一元二次方程：

（1）x（3x 4）=2（公式法）

（2）（2x 1）2﹣3（2x 1） 2=0

（3）mx2﹣（4m﹣1）x 3m﹣1=0（m≠0）

五、解答與證明（共33分）

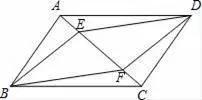
20．已知：如圖，在▱ABCD中，E、F是對角線AC上的兩點，且AE=CF．求證：四邊形BFDE是平行四邊形．

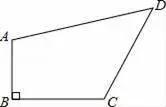
21．已知：如圖，四邊形ABCD中，AB⊥BC，AB=1，BC=2，CD=2，AD=3，求四邊形ABCD的面積．

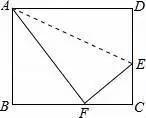
22．如圖，小紅用一張長方形紙片ABCD進行折紙，已知AB=8cm，BC=10cm．當小紅折疊時，頂點D落在BC邊上的點F處（折痕為AE），求EC．

23．已知：關于x的方程mx2 （3m 1）x 3=0．

（1）求證：不論m為任何實數，此方程總有實數根；

（2）如果該方程有兩個不同的整數根，且m為正整數，求m的值．

24．如圖，已知在△ABC中，DE∥BC交AC于點E，交AB于點D，DE=

BC .

求證：D、E分别是AB、AC的中點．

25．如圖，已知正方形ABCD和正方形AEFG，連結BE、DG．

（1）求證：BE=DG，BE⊥DG；

（2）連接BD、EG、DE，點M、N、P分别是BD、EG、DE的中點，連接MP，PN，MN，求證：△MPN是等腰直角三角形；

（3）若AB=4，EF=2

，∠DAE=45°，直接寫出MN=．

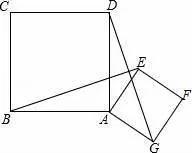
26．如圖，在正方形ABCD外側作直線DQ，點C關于直線DQ的對稱點為P，連接DP、AP，AP交直線DQ于點F，交BD于點E．

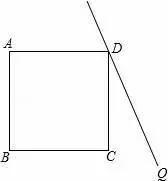
（1）依題意補全圖形；

（2）若∠QDC=25°，求∠DPA的度數；

（3）探究線段AE、EF、FP的等量關系并加以證明．

六、附加題：思維拓展（本題6分，計入總分）

27．已知直線y=

x 3分别交x軸、y軸于點A、B．

（1）求∠BAO的平分線的函數關系式；（寫出自變量x的取值範圍）

（2）點M在已知直線上，點N在坐标平面内，是否存在以點M、N、A、O為頂點的四邊形為菱形？若存在，請直接寫出點N的坐标；若不存在，說明理由．

關注初中數學微信公衆号，回複“423”獲取詳細解析！

更多精彩资讯请关注tft每日頭條，我们将持续为您更新最新资讯!