大家好，我是李工，希望大家多多支持我。

在前面我已經給大家介紹了三種振蕩器，Colpitts 振蕩器、皮爾斯振蕩器、哈特利振蕩器。如果錯過的話，可以點擊下方标題直接跳轉。

colpitts振蕩器電路圖分析，幾分鐘，立馬搞定colpitts振蕩器電路

皮爾斯振蕩器電路工作原理圖解，幾分鐘，立馬搞定皮爾斯振蕩電路

不會設計哈特利振蕩器？圖文 案例，手把手教你哈特利振蕩器設計

今天給大家講一下RC振蕩器。

使用電阻和電容元件的振蕩器可以獲得良好的頻率穩定性和波形，這種振蕩器稱為RC或者相移振蕩器。

RC振蕩器是一種正弦振蕩器，用于在線性電子元件的幫助下産生正弦波作為輸出。RC振蕩器包括一個反饋網絡和一個放大器。

RC 振蕩器的工作原理是利用 RC 網絡（如下圖所示）提供響應信号所需的相移的電路。

RC 振蕩器具有出色的頻率穩定性，可以為各種負載産生純正弦波。

下圖左邊的電路顯示了單個電阻電容網絡，其輸出電壓“超前”輸入電壓某個角度小于 90°。

在純或理想的單極 RC 網絡中，它将産生恰好為 90 °的最大相移，但由于振蕩需要 180 °的相移，因此在RC 振蕩器設計中必須使用至少兩個單極網絡。

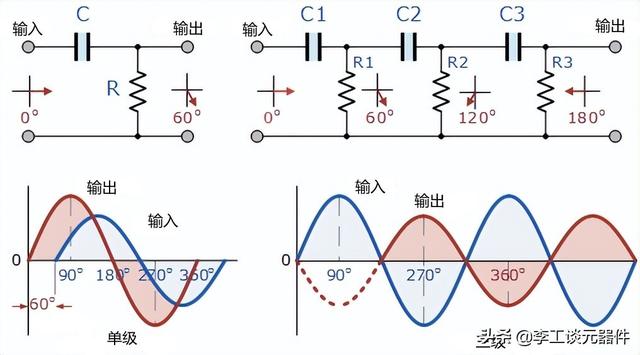
RC振蕩器相移網絡

然而，實際上每個 RC 級很難獲得準确的 90 °相移，因此我們必須使用更多級聯的 RC 級來獲得振蕩頻率所需的值。

電路中的實際相移量取決于電阻 (R) 和電容 (C) 的值，在選定的振蕩頻率下，相位角 ( φ ) 如下公式所示。

RC 相位角

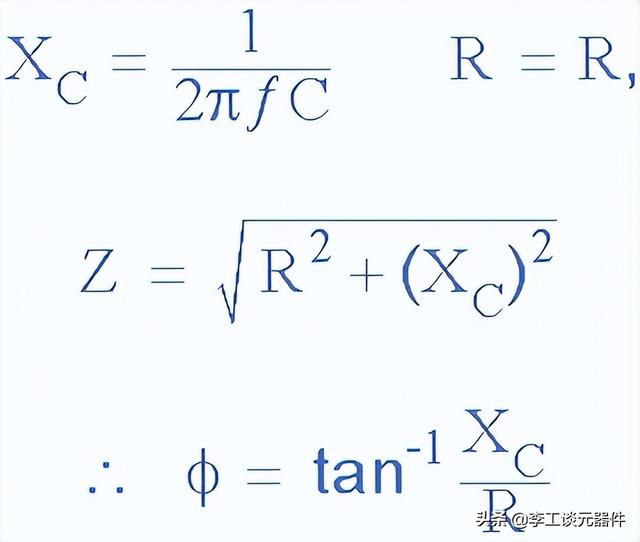
RC振蕩器相位公式

其中： X C是電容的容抗，R 是電阻的阻值，而ƒ是頻率。

在上面的簡單示例中，已選擇R和C的值，以便在所需頻率下，輸出電壓領先輸入電壓約 60 °的角度，然後每個連續 RC 部分之間的相位角再增加 60 °，從而在輸入和輸出之間産生 180 ° (3 x 60 ° )的相位差，如下面的矢量圖所示。

矢量圖

通過将三個這樣的 RC 網絡（如上圖右側）串聯在一起，我們可以在所選頻率下在電路中産生 180 °的總相移，這形成了“RC 振蕩器”的基礎，也稱為相移振蕩器，因為相角在通過電路的每個階段都移動了一定量。

相移發生在各個 RC 級之間的相位差中。運算放大器電路采用四路 IC 封裝，例如，LM124 或 LM324 等，因此四個 RC 級 也可用于在所需的振蕩頻率下産生所需的 180 °相移。

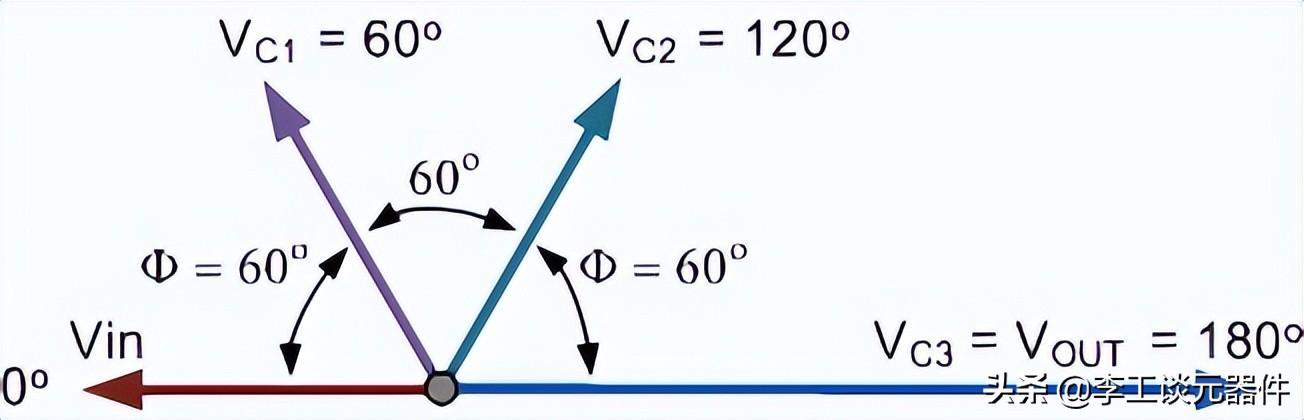
RC振蕩器矢量圖

在使用雙極晶體管或反相運算放大器配置的放大器電路中，它會在其輸入和輸出之間産生 180 °的相移。

如果三級 RC 相移網絡作為反饋網絡連接在放大器電路的輸出和輸入之間，則産生所需再生反饋的總相移為：3 x 60 ° 180 °= 360 ° = 0 °。如下圖所示。

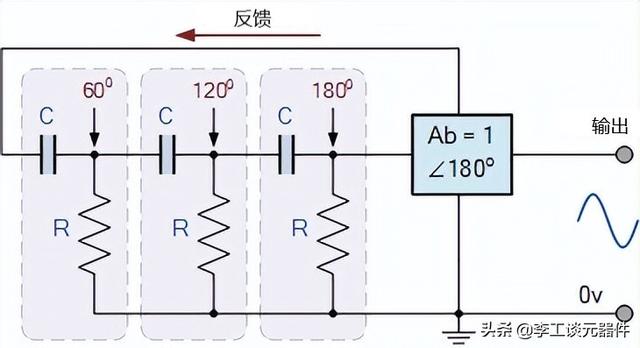
基本RC反饋電路

三個 RC 級級聯在一起以獲得穩定振蕩頻率所需的斜率。當每級相移為-60°時，反饋回路相移為-180 °。這發生在jω = 2piƒ = 1/1.732RC為 ( tan 60 °= 1.732 ) 時。

然後，要在 RC 振蕩器電路中實現所需的相移，就要使用多個 RC 相移網絡。

基本RC 振蕩器也稱為相移振蕩器，它使用從電阻電容 (RC) 梯形網絡獲得的再生反饋産生正弦波輸出信号。這種來自RC網絡的再生反饋是由于電容器能夠存儲電荷（類似于 LC 諧振電路）。

該電阻電容反饋網絡可以如上圖所示連接以産生超前相移（相位超前網絡）或互換以産生滞後相移（相位延遲網絡）結果仍然相同，因為正弦波振蕩僅發生在總相移為 360 °的頻率。

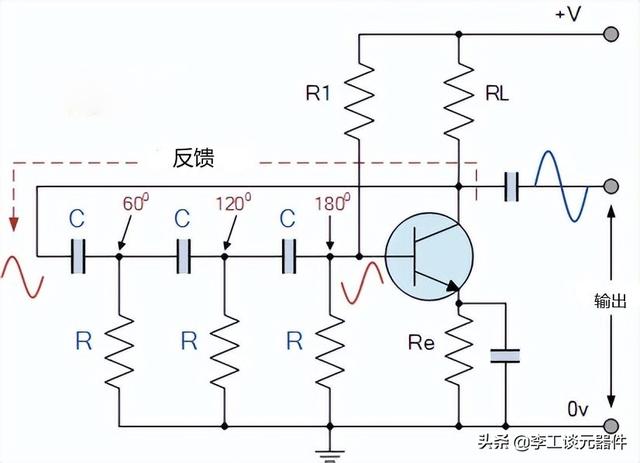
RC振蕩電路設計

通過改變相移網絡中的一個或多個電阻或電容，可以改變頻率，通常這是通過保持電阻器相同并使用 3 組可變電容來完成的。

因為容抗 (X C ) 随電容變化，由于電容是頻率敏感元件，因此頻率會發生變化。但是，可能需要針對新頻率重新調整放大器的電壓增益。

如果三個電阻 R 的值相等，即R 1 = R 2 = R 3 ，并且移相網絡中的電容 C 的值也相等， C 1 = C 2 = C 3，則頻率由 RC 振蕩産生的振蕩簡單地給出為：

RC振蕩器頻率公式

• ƒ r 是以赫茲為單位的振蕩器輸出頻率
• R 是歐姆的反饋電阻
• C 是以法拉為單位的反饋電容
• N 是RC反饋級數。

這是相移電路振蕩的頻率，上面的簡單示例中，級數為 3，因此 N = 3 (√ 2*3 = √ 6 )。對于四級 RC 網絡，N = 4 (√ 2*4 = √ 8 ) ，其他的依此類推。

當用作 RC 振蕩器時，運算放大器 RC 振蕩器比其雙極晶體管振蕩器更常見。振蕩器電路由負增益運算放大器和産生 180 °相移的三段RC網絡組成。相移網絡從運算放大器輸出連接回其“反相”輸入，如下所示。

由于反饋連接到反相輸入，因此運算放大器連接在其“反相放大器”配置中，該配置産生所需的 180 °相移，而RC網絡在所需頻率（180 ° 180 °）。

這種與串聯電容器和連接到地 (0V) 電位的電阻器的反饋連接稱為相位引線配置。

換句話說，輸出電壓超前于輸入電壓，産生一個正相角。

我們也可以通過簡單地改變 RC 組件的位置來創建相位滞後配置，使電阻串聯連接，電容連接到地 (0V) 電位，如下圖所示。這意味着輸出電壓滞後于輸入電壓，從而産生負相角。

運算放大器相位滞後 RC 振蕩器電路

然而，由于反饋分量的反轉，相位超前 RC 振蕩器的頻率輸出的原始方程被修改為：

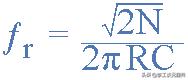
RC振蕩電路頻率公式

盡管可以僅将兩個單極RC級級聯在一起以提供所需的 180 相移 (90 ° 90 ° )，但振蕩器在低頻下的穩定性通常很差。

RC 振蕩器最重要的特性之一是其頻率穩定性，即它能夠在變化的負載條件下提供恒定頻率的正弦波輸出，通過将三個甚至四個RC級級聯在一起（4 x 45 °），可以大大提高振蕩器的穩定性。

通常使用具有四級的RC 振蕩器，因為常用的運算放大器采用四路 IC 封裝，因此設計一個相對于彼此具有 45 °相移的 4 級振蕩器相對容易。

RC 振蕩器是穩定的，并提供形狀良好的正弦波輸出，其頻率與1/RC成正比，因此，使用可變電容時可以實現更寬的頻率範圍。然而，RC 振蕩器受限于頻率應用，因為它們的帶寬受限，無法在高頻下産生所需的相移。

現在需要一個基于運算放大器的3 級 RC 相移振蕩器來産生 4kHz 的正弦輸出頻率，如果在反饋電路中使用 2.4nF 電容，請計算頻率确定電阻的值和維持振蕩所需的反饋電阻的值，還要畫出電路。

相移 RC 振蕩器的标準方程為：

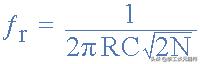
RC振蕩器頻率

該電路将是一個 3 級 RC 振蕩器，因此将由相等的電阻和三個相等的 2.4nF 電容組成。由于振蕩頻率為 4.0kHz，因此電阻值計算如下：

運算放大器增益必須等于 29 才能維持振蕩。振蕩電阻的阻值為6.8kΩ，因此運算放大器反饋電阻R ƒ的值計算如下：

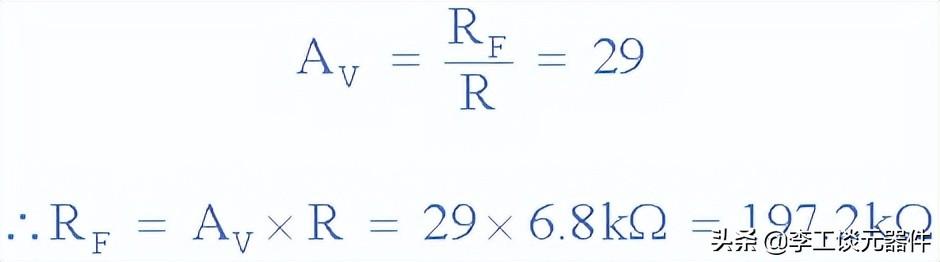
反饋電阻R ƒ

RC 振蕩器運算放大器電路如下圖所示：

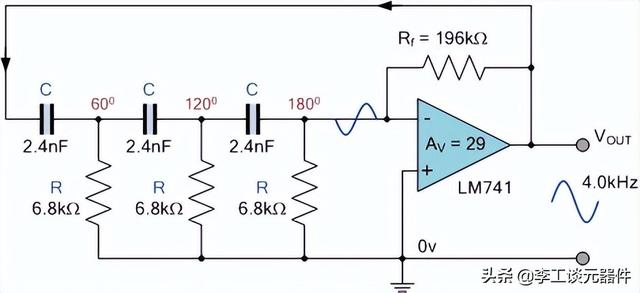
RC 振蕩器運算放大器電路

使用BJT的 RC 相移振蕩器如下圖所示。該電路中使用的晶體管是放大級的有源元件。晶體管有源區域内的直流工作點可由 Vcc 電源電壓和 R1、R2、RC 和 RE 電阻設置。

使用 BJT 的 RC 相移振蕩器

CE 電容是一個旁路電容，在這裡，三個 RC 段被視為相等。

R1 和 R2 電阻是偏置電阻，它們性能優越，因此對交流電路的運行沒有影響。此外，由于 RE-CE 的組合可獲得微不足道的阻抗，因此對交流操作也沒有影響。

當向電路供電時，噪聲電壓開始在電路内振蕩。在晶體管放大器上，一個小的基極電流放大器産生一個可以相移180° 的電流。

每當這個信号響應放大器的輸入時，它就會再次被移相 180 °。如果環路的增益等于 1，則将産生持續的振蕩。

該電路可以通過使用等效交流電路來簡化，然後我們可以得到如下所示的振蕩頻率：

f = 1/ (2πRC √ ((4Rc / R) 6))

當 Rc / R << 1 時，則

f= 1/ (2πRC√ 6)

從上述等式中，為了改變振蕩頻率，必須改變電容和電阻的值。

然而，為了滿足振蕩的條件，三段值應該同時改變。實際上，這是不可能的，因此，RC 振蕩器就像固定頻率振蕩器一樣用于各種實際用途。

• 由于沒有昂貴且體積龐大的高價值電感，電路設計簡單，非常适合低頻範圍
• 可以産生較為純正弦波形
• 固定在一個頻率上，良好的頻率穩定性
• 成本也非常低，因為它包含成本不高的電阻和電容
• 輸出是正弦的，所以輸出沒有失真
• 不需要穩定裝置和負反饋
• 具有廣泛的頻率範圍，即從幾赫茲到幾百赫茲
• 自啟動，使用反饋來啟動振蕩并最終達到動态平衡
• 低噪聲，如果布局正确，系統的噪聲會受到運算放大器噪聲功率譜密度的限制
• 可調增益，與任何其他運算放大器電路一樣，可以通過将反饋電阻設置為适當的值來選擇輸出增益

• 反饋較小，輸出也非常少
• 在輸出中産生 5% 的失真水平
• 增益受限，RC振蕩器電路需要高增益，但實際上是不可能的
• 由于各種電路元件的溫度、老化等影響，頻率穩定性較差
• 反饋很小，電路開始振蕩有點困難
• 需要高壓電池來産生大而足夠的反饋電壓
• 帶寬受限，運算放大器的帶寬限制了高頻下的可用增益，超出單位增益帶寬，增益将降至 0 dB 以下

以上就是關于RC振蕩器的一些内容，希望能夠對大家有幫助。

圖片來源于網絡

更多精彩资讯请关注tft每日頭條，我们将持续为您更新最新资讯!