例 1 證明對角行列式（其中對角線上的元素是，未寫出的元素都是0）
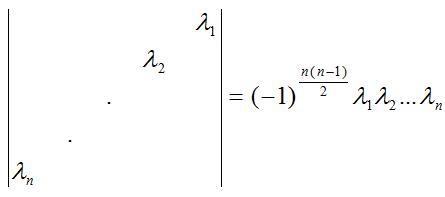
證 第一式是顯然的，下面隻證第二式。
若記，則依行列式定義
,
其中為排列的逆序數，故。 證畢。
兩個對角陣，我們可以理解為n維的正超立方體，隻不過兩者向量的方向不同。至于正負号的問題，我們有個簡單的判斷方法。以列為向量空間的維度數，從左到右設為1、2、...、n維，從1維到n維算起，向量坐标值的符号不變；從n維到1維算起，向量坐标值都取它的相反數，那麼，偶數階行列式不變号，奇數階行列式變負号（2階行列式除外）。
例2
對角線以下（上的元素都為0的行列式）叫做上（下）三角行列式，它的值與對角行列式一樣。
證明下三角行列式
證 由于當時，，故中可能不為0的的元素，其下标應有，即。
在所有排列中，能滿足上述關系的排列隻有一個自然排列12...n，所以中可能不為0的項隻有一項，此項的符号，所以。
任一元素的行、列标的組合是123...n對123...n的兩兩配對。以自然排列的情形為基礎，互換兩個列标，比如1、4互換，就會出現14和41兩個配對。那樣肯定有列标比行标大的情況。而在三角行列式中，當列标大于行标時，元素是0。那麼，除了自然排列外，所有的排列都是0。
例3 設
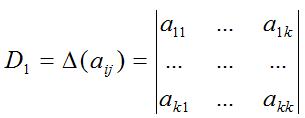
證明 。
證 記，其中
。
考察的一般項
,
由于當時，，因此隻有在中選取時，該項才可能不為0，而當在中選取時，隻能在中選取。于是中可能不為0的項可以記作
，
這裡，，而為排列的逆序數，以分别表示排列及的逆序數，應有。于是
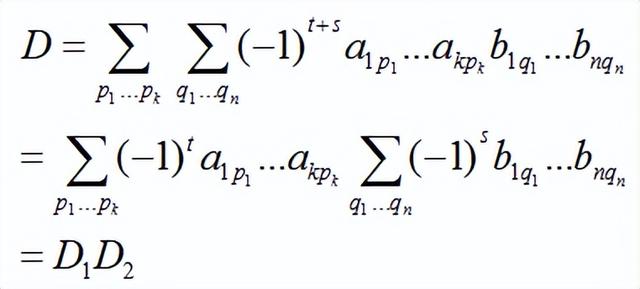
這裡面有點繞啊。我們先不看排列本身，而是看一個排列裡面行标與列标的兩兩配對，行、列标都是12...k...n。有行标1~k配列标k~n，肯定就有列标1~k配行标k~n，所以在一個排列裡，有ab的地方一定有c0，除非ab能把這個排列占滿。
那麼，所有排列可以分三類，ab排列、abc0排列，c0排列，隻ab排列不為0。
,更多精彩资讯请关注tft每日頭條，我们将持续为您更新最新资讯!
zpostcode 
Recruit 
weather 
mreligion 
Yellowpages 
sport 
constellation 
shopping 
name 
game 
directory 
literature 
Word 
tour 
furnish 
Lottery 
tftnews 
lyrics 
News 
digital 
car 
dir 
Edu 
Finance 
