随機變量及其概率分布講解-tft每日頭條

随機變量及其概率分布講解

生活更新时间:2024-11-27 01:32:58

分布函數的定義：

對于任意實數x，記函數F(x)=P{X<=x},x取值範圍實數全集，稱F(x)為随機變量X的分布函數。

分布函數F(x)是定義在實數集上的一個實值函數，F（x）的值即為事件“X<=x”的概率。

分布函數的性質：

分布函數具有如下性質：

随機變量及其概率分布講解（概率論與數理統計之随機變量及其分布函數知識點總結）1

分布函數的性質

題型一：利用分布函數的性質求參數的值

例1：

随機變量及其概率分布講解（概率論與數理統計之随機變量及其分布函數知識點總結）2

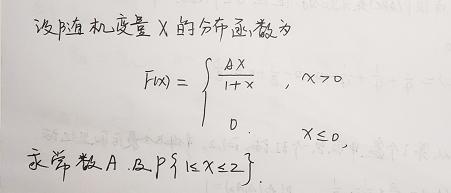
解題思路：利用分布函數的性質來解題，這是考研中經常考察的題型。

解：由分布函數的性質得：

随機變量及其概率分布講解（概率論與數理統計之随機變量及其分布函數知識點總結）3

題型二：已知分布函數，求随機變量在一點的概率值

例2：

随機變量及其概率分布講解（概率論與數理統計之随機變量及其分布函數知識點總結）4

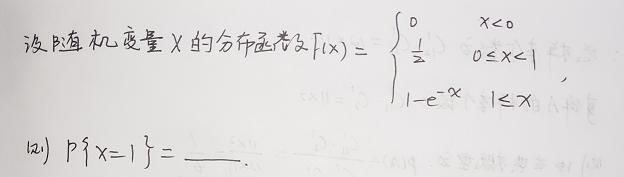
解題思路：根據分布函數的性質來計算。

解：根據分布函數性質5可得：

随機變量及其概率分布講解（概率論與數理統計之随機變量及其分布函數知識點總結）5

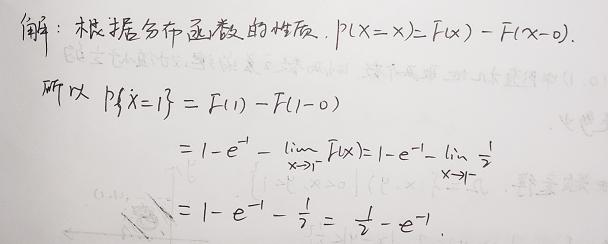
總結：本節需要熟練掌握分布函數的性質，分布函數的性質是考研中經常考察的知識點，需要重點掌握。

更多精彩资讯请关注tft每日頭條，我们将持续为您更新最新资讯!

查看全部

网友关注

生活持倉盈虧和累計盈虧的區别是什麼
1、從性質上說，持倉損益是當前賬戶整體所持倉庫發生的損益，累計損益是一定期間内賬戶整體的損益水平。2... 2023-06-28
生活怎麼存放楊桃
1、常溫下：楊桃在常溫下，它會迅速的變軟、失水、腐爛，所以我們采摘下楊桃後，一定要及時的儲存，防止變... 2023-06-28
生活怎麼申請面試成績審核
1、從2019下半年各省發布的教師資格面試考試公告當中的内容來看，考生若對成績有異議，可以申請成績複... 2023-06-28
生活電腦上怎麼截屏發給别人
1、使用快捷鍵：先把需要截圖的畫面調出來，在鍵盤上找到“PrtscSysRq”鍵并點擊，即可把整個頁... 2023-06-28
生活在人耳處減少噪音的方法有哪些
1、對付噪音的最好辦法就是窗戶要嚴封，不管是單層窗還是雙層窗，密封是最主要的。木桶的承載量是由最短的... 2023-06-28
生活怎麼在蘋果平闆上玩電腦闆我的世界
1、因為蘋果系統是需要專用的AppStore商店下載應用的，所以我們需要打開iPad上的AppSto... 2023-06-28
生活香奈兒香水5号有幾款香奈兒5号香水的...
2023-06-28
生活簡單方法自制火柴
1、首先我們要準備質量好的火柴，蠟燭，和紙。2、點燃蠟燭将蠟燭油滴在紙上。3、用蠟燭将紙上的蠟燭塗抹... 2023-06-28
生活怎麼樣瘦肚子最快最有效
1、跑步跑步是健身中最有效的減肥方式，跑步不僅能減去肚子上的贅肉，而且能讓全身都處于運動狀态，想要減... 2023-06-28
生活草酸能除鏽嗎
2023-06-28
生活農村合作醫療是醫保嗎
農村合作醫療是針對農村人口推行的醫保保障政策、福利，農村合作醫療僅屬于醫保的一部分，醫保還包括城鎮居... 2023-06-28
生活全棉時代是哪裡生産的
1、全棉時代是在深圳生産的。2、全棉時代是指深圳全棉時代科技有限公司是穩健醫療集團的子公司，全棉時代... 2023-06-28
生活筋膜槍是智商稅嗎怎麼使用才能起到按摩...
2023-06-28
生活阿裡怎麼搜索産品
1、直接輸入名稱：阿裡作為一個電商的網站很多的東西，和淘寶都是一樣的，就拿搜索來說，直接要什麼就搜什... 2023-06-28
生活冬季面試怎麼穿
1、技巧一：大衣+修身版長褲+短靴經典的雙排扣紅色呢子大衣，高腰線的設計，非常顯高。大口袋，小圓領更... 2023-06-28
生活荸荠煮多久殺死寄生蟲
1、荸荠煮10分鐘可以殺死寄生蟲。2、寄生蟲的主要成分是蛋白質和水分，不耐高溫，很容易煮熟，蛋白質在... 2023-06-28
生活個人如何開啟網課
1、首先，我們填好用戶名和密碼的信息，接着點擊“登錄”按鈕，登錄自己的學習賬号上去。2、接着，我們登... 2023-06-28
生活凡爾賽尾款人是什麼意思
1、通過付尾款這件事情，用反向的表述不經意透露出自己高貴、奢華的生活。2、例如：一想到還要付2億的尾... 2023-06-28
生活京東打白條後怎麼還款京東白條開了可以...
2023-06-28
生活 12329人工時間
2023-06-28
生活北方的蟑螂會飛嗎
2023-06-28
生活深秋釣鲢鳙方法
1、一是釣位要選對深秋釣位應選擇淺水與深水的過渡段水域，或鲢鳙魚常遊弋的水段及水路；如果沒有明顯的魚... 2023-06-28
生活微信朋友圈動态不顯示怎麼辦
1、首先打開手機，打開手機裡的微信，找到“我”的界面。2、然後打開“設置”選項。3、之後再選擇打開“... 2023-06-28
生活好聽的微信昵稱男生霸氣
1、傲氣逼人2、路還長别太狂3、請注意你的素質4、很酷很霸氣5、别講道理砍他6、爺′狠潇灑7、冷劍狂... 2023-06-28
生活鹌鹑蛋一天吃幾個合适
1、鹌鹑蛋是一種營養價值非常高的蛋，其營養含量遠高于雞蛋。通常，一天吃三個就足夠了，這樣就可以有效地... 2023-06-28
生活五岔路口怎麼看紅綠燈
2023-06-28
生活被辣椒水噴眼睛怎麼辦
1、如果辣椒水進到眼睛，緊急處理的辦法是用流動的自來水沖洗，沖洗的時間要稍微長點，或者把患者送到醫院... 2023-06-28
生活小米路由器開dns上不了網
1、如果你路由器設置了MAC白名單卻忘了綁自己的設備，那絕對就會出現這種情況，這時進入路由器設置MA... 2023-06-28
生活龍井茶的功效與作用龍井的營養價值
2023-06-28
生活空調制熱30度還是不熱怎麼解決
1、空調長期不清理：過濾網的作用是吸附空氣中的灰塵，如果長期得不到清理，過濾器積塵太多、會使内外機通... 2023-06-28

tft每日頭條

> 生活

> 随機變量及其概率分布講解

随機變量及其概率分布講解

相关生活资讯推荐

热门生活资讯推荐

网友关注