在數資中容斥問題是高頻考點之一

今天，小編和大家分享

容斥問題的兩大重點題型

快來和小編開啟今日份學習之旅吧~

容斥問題是曆年的常考題型, 也是小夥伴們的的得分重點。該類題目中會給出多個條件(概念), 各條件(概念) 之間存在交叉關系。

例如: 某班參加物理競賽的有30 人, 參加數學競賽的有32 人, 兩科都參加的有20 人。在這裡物理競賽是第一個條件, 數學競賽是第二個條件, 滿足第一個條件和第二個條件的人數分别是30 人和32 人, 同時兩科都參加的有20 人, 這20 人是即參加物理競賽又參加數學競賽的, 說明物理競賽和數學競賽存在交集。

通過以上描述可知, 在做題的過程中, 要知道容斥問題的題目特征是非常重要, 同時确定了題型之後我們要知道如何解決這類問題。容斥問題在考試中考查兩大類題型:兩集合和三集合。這兩類題型都有相應的公式, 以及需要我們注意的問題。快來和小編一起破解這兩大類題型吧~

【例1】（2019江蘇）市電視台向150位觀衆調查前一天晚上甲、乙兩個頻道的收視情況, 其中108 人看過甲頻道, 36 人看過乙頻道, 23 人既看過甲頻道又看過乙頻道, 則受調查觀衆中在前一天晚上兩個頻道均未看過的人數是:

A. 17 B. 22 C. 29 D. 38

【答案】C

【解析】

第一步，本題考查容斥原理中的二集合容斥原理，用公式法解題。

第二步，設受調查觀衆中在前一天晚上兩個頻道均未看過的人數為x，根據二集合容斥原理公式可列方程：108＋36－23＝150－x，解得x＝29。因此，選擇C選項。

【例2】(2018年聯考)某試驗室通過測評Ⅰ和Ⅱ來核定産品的等級: 兩項測評都不合格的為次品, 僅一項測評合格的為中品, 兩項測評都合格的為優品。某批産品隻有測評Ⅰ合格的産品數是優品數的2 倍, 測評Ⅰ合格和測評Ⅱ合格的産品數之比為6 ∶ 5。若該批産品次品率為10%, 則該批産品的優品率為:

A. 10% B. 15% C. 20% D. 25%

【答案】C

【解析】

第一步，本題考查容斥問題，屬于二集合容斥類。

第二步，賦值優品數為2，則隻有測評Ⅰ合格的為4，那麼測評Ⅰ合格的為6。根據合格之比為6∶5，可推知測評Ⅱ合格的為5，則隻有測評Ⅱ合格的為5－2＝3，那麼合格的為6＋5－2＝9，由産品次品率為10%，可知合格率為90%。則不合格産品為1，總數為10。

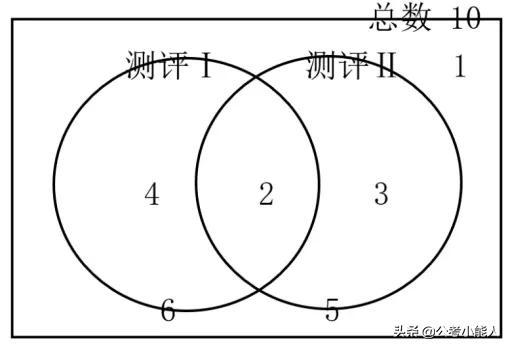
第三步，該産品的優品率為2/10=20%

因此，選擇C選項。

【例3】（2020年新疆）某單位共有240名員工, 其中訂閱A 期刊的有125 人, 訂閱B 期刊的有126 人, 訂閱C 期刊的有135 人, 訂閱A、B 期刊的有57 人, 訂閱A、C 期刊的有73人, 訂閱3 種期刊的有31 人, 此外, 還有17 人沒有訂閱這三種期刊中的任何一種。問訂閱B、C 期刊的有多少人?

A. 57 B. 64 C. 69 D. 78

【答案】B

【解析】

第一步，本題考查容斥原理。

第二步，題目中滿足兩個條件的集合人數是分别給出的，應用三集合标準型容斥原理公式解題。設訂閱B、C期刊的有x人，可列方程：125＋126＋135－57－73－x＋31＝240－17，解得x＝64（也可利用尾數法求得尾數為4）。

因此，選擇B選項。

【例4】（2019年河北）某班參加學科競賽人數40人, 其中參加數學競賽的有22 人, 參加物理競賽的有27 人, 參加化學競賽的有25 人, 隻參加兩科競賽的有24 人, 參加三科競賽的有多少人?

A. 2 B. 3 C. 5 D. 7

【答案】C

【解析】

第一步，本題考查容斥問題，屬于三集合容斥類，用公式法解題。

第二步，設參加三科競賽的有x人，根據三集合非标準型容斥原理公式可列方程：40－0＝22＋27＋25－24－2x，解得x＝5。

因此，選擇C選項。

以上就是今天的備考技巧

覺得不錯的話

記得幫小編點個贊＋關注呦

也可私信小編領取更多公考資料

更多精彩资讯请关注tft每日頭條，我们将持续为您更新最新资讯!