正切函數的圖象
8等分法作正切曲線
01
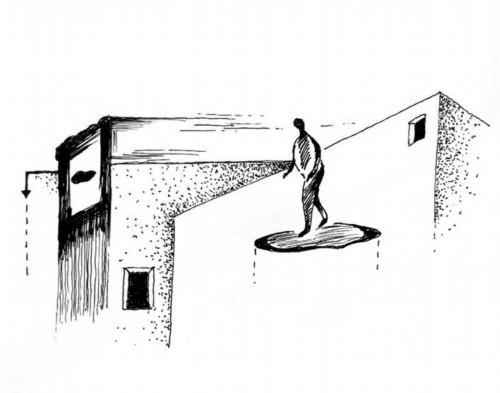
将單位圓（-π/2，π/2）間的半圓弧8等分，同時将x軸上的區間（-π/2，π/2）作8等分，将角x對應的正切線向右平移，使它的起點與x軸上表示數x的點重合，再把這些互切線的終點用光滑的曲線連接起來，就得到正切函數在（-π/2，π/2）上的圖象，最後根據正切函數的周期性，把所得到的圖象向左、右平移π 的整數倍，就得到y=tanx的圖象，我們把它叫做正切曲線.
拓 展
（1）不用等分法，直接動态展示由正切線生成正切曲線的過程如下（觀察白線）：
正切線生成正切曲線
（2）同樣地，生成正弦曲線（觀察藍線）、餘弦曲線（觀察紅線）對應的過程分别如下：
正弦線到正弦曲線
餘弦線到餘弦曲線
“三點兩線法”快速畫正切函數的簡圖
02
先畫出直線x=±π/2作為正切函數圖象的漸近線，然後根據三個特殊點（-π/4，-1），（0，0），（π/4，1）及對正切函數圖象的認識畫出草圖，最後，由周期性畫出整個正切函數圖象的草圖.
動圖如下：
三點兩線畫正切
敲黑闆！看重點！
（1）正切函數在(-π/2 kπ，π/2 kπ)（k∈Z）上遞 增 ，不能寫成閉區間；
（2）正切函數沒有單調 減 區間.
正切曲線是被相互 平行 的直線x=π/2 kπ，k∈Z（稱為漸近線）所隔開的無窮多支曲線組成的，即正切函數有 無數 多條漸近線，漸近線方程為x=π/2 kπ，k∈Z，相鄰兩條漸近線之間都有一條正切曲線，且單調遞增.
正切函數與正弦函數的異同點
【示範例題】
例題1.(解析題)觀察正切曲線，寫出滿足下列條件的x的取值範圍.
tan x>0;tanx=0;tanx<0
【答案】見解析
【解析】使用“三點兩線法”快速畫出y=tanx，-π/2<x<π/2的簡圖，觀察圖象可得，當0<x<π/2時，tanx>0，故所求的的取值範圍為(kπ，kπ π/2），k∈Z.
同理可得tanx=0的x的取值範圍為﹛x|x=kπ,k∈Z﹜；
tanx<0的x的取值範圍為(kπ-π/2，kπ），k∈Z.
【破題】先用“三點兩線法”快速畫出正切函數的簡圖，再利用圖象解決問題.
内容摘自：包學習APP_動态教輔《正切函數的性質與圖象（高中數學必修四1.4.3）》，歡迎下載學習更多知識
本文轉載自包學習網站。
曆史使人聰明詩歌使人機智數學使人精細包學習APP溫馨提示大家：掌握得高分，細心才能得滿分呦！在函數學習中每一個符号都很重要！要認真審題和仔細答題哦~~
更多精彩资讯请关注tft每日頭條，我们将持续为您更新最新资讯!
zpostcode 
Recruit 
weather 
mreligion 
Yellowpages 
sport 
constellation 
shopping 
name 
game 
directory 
literature 
Word 
tour 
furnish 
Lottery 
tftnews 
lyrics 
News 
digital 
car 
dir 
Edu 
Finance 
