這篇連連看教程我嘗試換一種方式，多講一些算法思路和編程思想，少貼一些代碼。

大家應該都玩過連連看，遊戲規則不多說了，我們先看看設計思路。

第一件事要根據遊戲玩法确定程序的數據結構，不同的數據結構決定了不同的算法設計，用錯了數據結構可能直接讓代碼複雜好幾倍。

連連看中玩家操作的數據是一個個的圖片，多個圖片組成一個棋盤式的矩陣界面。程序根據玩家的點擊位置計算兩個圖片的連接路線，這要求程序以最快、最簡單的方式獲得矩陣中每個格子的數據。

用二維數組表示遊戲中的矩陣界面比較合适，因為數組可以通過索引快速訪問數據，二維數組的兩個索引剛好對應矩陣界面的(x, y)坐标。例如：

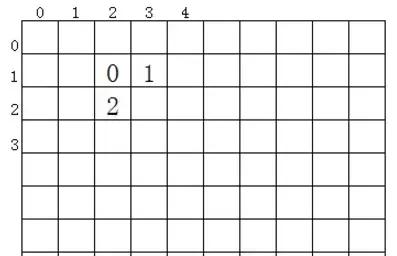
圖中矩陣數據在代碼中應該這樣表示：

可以用不同的數字代表不同的圖片，比如：

那麼上面的矩陣繪制的時候就會是這樣：

0表示空格，不顯示圖片。初始化時的空格或消除後的空格，都會被設置為0。

接下來要初始化數據，我打算用8種不一樣的圖片，每種6張，随機放入矩陣中，矩陣最外一圈是空的。這個算法可以用标準庫函數 std::random_shuffle 來完成。std::random_shuffle 用于把容器内的數據随機打亂，因此按順序把數據放入數組中，然後調用 std::random_shuffle 就可以完成初始化。

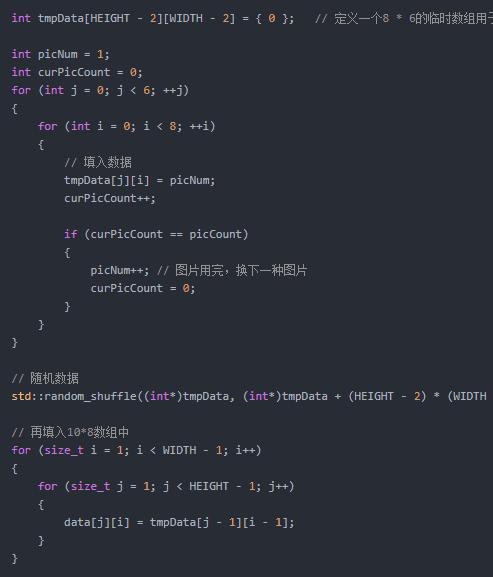
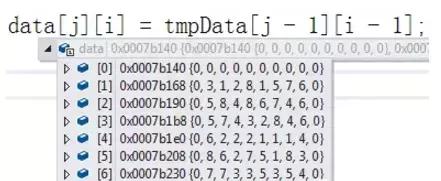
斷點運行觀察數組數據，和我們設計的一樣：

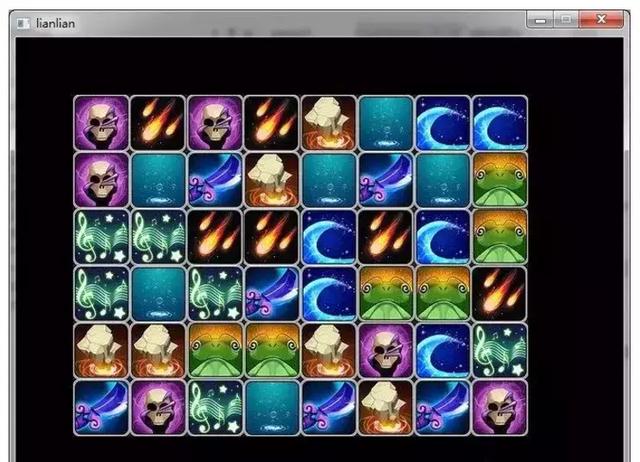
貼上圖片看起來還不錯：

現在來分析遊戲玩法。這個遊戲的難點是兩個圖片連接的判定算法，要求連接線隻能轉折兩次。

我的第一反應這是一個尋路算法，要求找到轉折兩次以下的最短路徑。教科書上常見的廣度優先搜索、深度優先搜索、DijKstra算法或是遊戲中常用的A星算法，稍作修改加上兩次轉折的限制都能解決這個問題。

但是如果我用這些比較複雜的算法來教新手，顯然是在勸退。所以還是考慮找一找連線判定的算法有沒有簡單的規律。

多玩幾次遊戲，把不同種類的連線記錄下來，總結後可以發現總共有3種連線類型，分别是不轉折連接、轉折一次和轉折兩次。

還是從最簡單的情況開始考慮。這是解決難題的通用方法：從最簡單的情況開始考慮，再逐步增加複雜的條件。

最簡單的不轉折連接，有兩種情況，橫向連線和縱向連線：

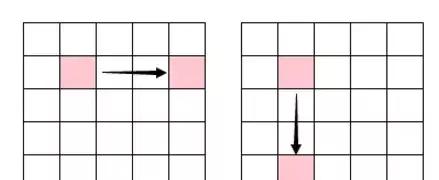
這兩種情況很容易處理，橫向、豎向依次檢查每個格子是否被阻擋即可。

最後把這兩個合并就是不轉折的情況下：

轉折一次：

轉折一次的算法也是比較明顯的，像上圖中的兩種情況，找到綠色點的位置，如果這個點可以不轉折連到兩個紅色的圖片，那麼這兩個紅色的圖片就可以通過一次轉折連接。

綠點的位置是由兩個紅點決定的，隻有上圖中的兩種可能。

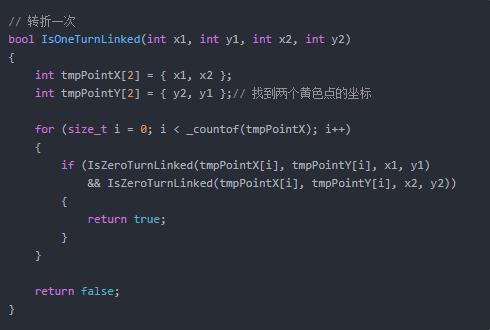
轉折兩次的情況就多了，下圖同樣是連接紅色圖片，要繞過綠色圖片。

轉折兩次的情況很多，這裡無法一一列舉，但是仔細思考可以發現和轉折一次本質上是一樣的，就是找到兩個點，這兩個點可以分别和紅色圖片無轉折連接，并且這兩個點也可以無轉折連接。

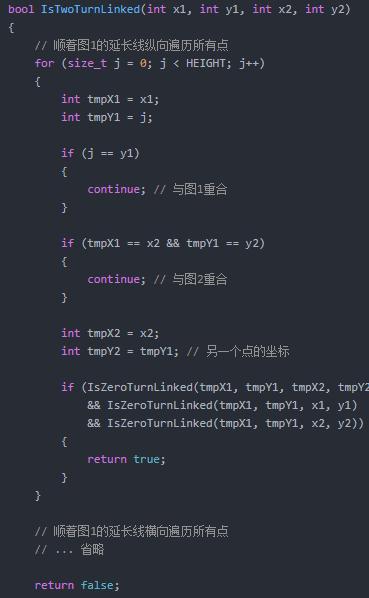
這兩個點需要位于經過紅色圖片的十字線上，并且隻要确定一個了其中一個點，就能對應地找到另一個點：

因此隻要遍曆其中一個圖片的兩條十字線經過的所有的點，并計算出另一個圖片十字線上對應點的位置，檢查這兩個點和兩個紅色圖片是否可以無轉折連接：

代碼碼完了，添上圖片和鼠标檢測的代碼跑一跑試試。

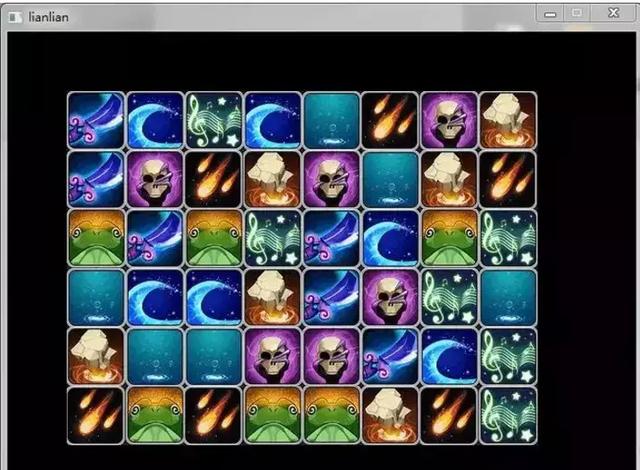
右邊顯示臨時顯示字符用于測試連通性，多次測試沒有問題。

最後加上連線，并清除被點擊的兩個格子，就完成了連連看的核心邏輯。你學會了嗎？

最後，想要成為一個優秀的程序員，最最重要的是盡可能的提升自己的編程能力以及編程思維，并且，與其想着怎麼去提升，不如從現在開始動手動腦，如果對于C/C 感興趣的話，可以加q。569，268，376，學習不怕從零開始，就怕從不開始。

,

更多精彩资讯请关注tft每日頭條，我们将持续为您更新最新资讯!

查看全部