一道初中幾何題-求梯形的面積
等腰梯形ABCD的兩個底為AB和CD，AB<CD, 腰AD=BC，點A到BC， CD和BD的距離分别是15， 18和10， 求梯形的面積。
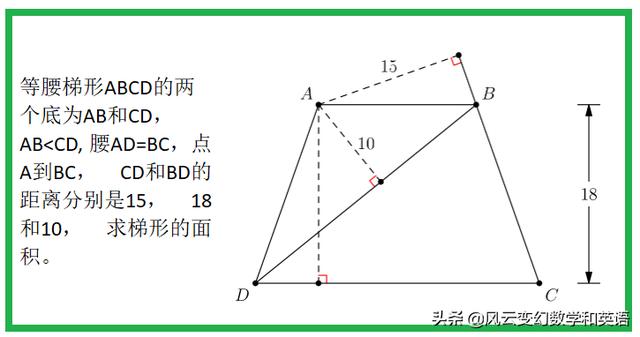
解： 如圖，設上底AB=x, 高線AF與BD的交點為H， 并AH=y,
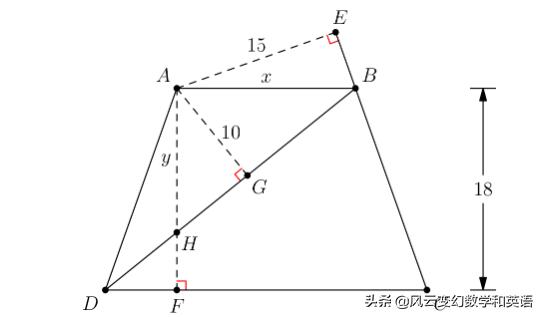
顯然HF=18-y,
根據勾股定理有：
以及：
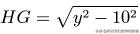
因為三角形ABG相似于三角形HAG，所以：
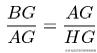
所以有：
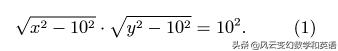
另外三角形AHB相似于三角形HFD，所以：
帶入後：
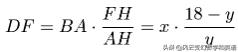
此外，由于是等腰梯形，相對應的一個底角等于對頂的外角，所以三角形EBA和三角形FDA相似：
帶入數值：
在三角形ADF利用勾股定理有：
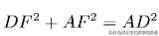
即：
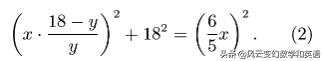
将方程1和2聯立可以解出：
即上底：
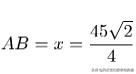
和下底：
最後梯形的面積為：
解法2： 如圖，
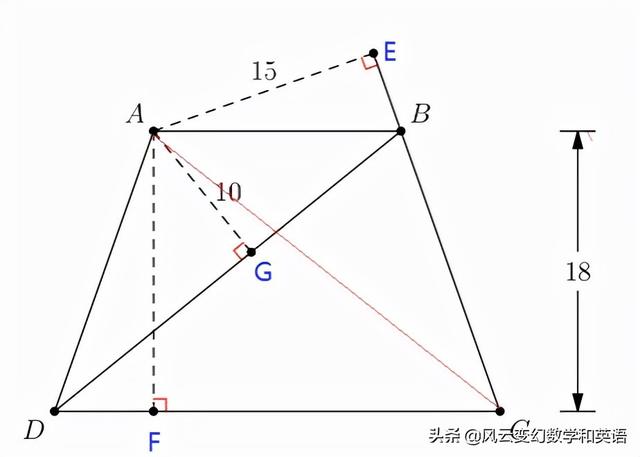
設三個垂足分别是E， F和G， 顯然這裡存在兩對相似的三角形， 分别是三角形ADF相似于三角形ABE， 以及三角形ADG相似于三角形ACE。
此外這裡需要兩個引理：
由此設AD=a,
根據相似性可以求出：
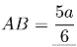
以及：
根據托勒密定理：
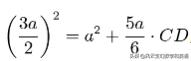
得出:
因此：
在三角形ADF中利用勾股定理：
解得：
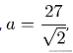
最後梯形的面積：
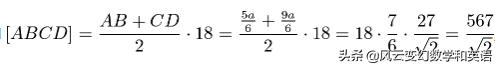
更多精彩资讯请关注tft每日頭條，我们将持续为您更新最新资讯!
zpostcode 
Recruit 
weather 
mreligion 
Yellowpages 
sport 
constellation 
shopping 
name 
game 
directory 
literature 
Word 
tour 
furnish 
Lottery 
tftnews 
lyrics 
News 
digital 
car 
dir 
Edu 
Finance 
