-1-
微積分(Calculus)是微分學(Differentiation)和積分學(Integration)的總稱,微分學就是‘無線細分’,積分學就是‘無限求和’,無限就是極限,微積分的基礎就是極限的思想。微積分是建立在實數、函數和極限的基礎上的,主要内容包括極限、連續、可微和重積分,最重要的思想就是“微元”和“無限逼近”。
微積分主要包括極限、微分學、積分學及其應用。微分學包括求導數的運算,是一套關于變化率的理論。它使得函數、速度、加速度和曲線的斜率等均可用一套通用的符号進行讨論。積分學,包括求積分的運算,為定義和計算面積、體積等提供一套通用的方法。
到了十七世紀,有許多科學問題需要解決,這些問題也就成了促使微積分産生的因素。歸結起來,大約有四種主要類型的問題:
第一類是研究運動的時候直接出現的,也就是求即時速度的問題。
第二類問題是求曲線的切線的問題。
第三類問題是求函數的最大值和最小值問題。
第四類問題是求曲線長、曲線圍成的面積、曲面圍成的體積、物體的重心、一個體積相當大的物體作用于另一物體上的引力。
用數學的語言描述這一概念,我們定義直線的斜率為:
如果一條直線的斜率是2/5,那麼當x增加5個單位時,y會增加2個單位,緩緩上升。但如果斜率是5/2,則表明當x增加2個單位時,y整整增加了5個單位,此時攀升速度相當快。
通過點(x1,y1)和點(x2,y2)的直線的斜率的定義:

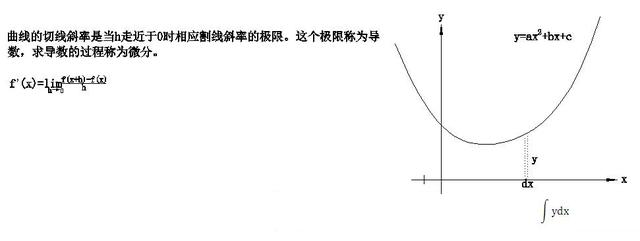
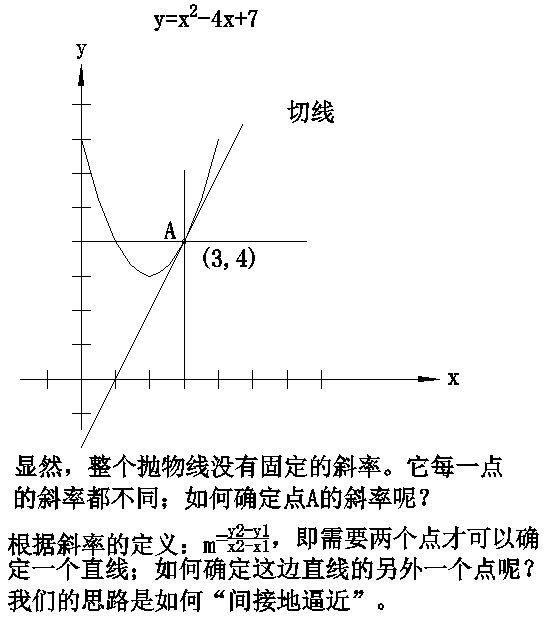
如何确定曲線的斜率呢?如y=4x^2 2x 9,顯然,整個抛物線沒有固定的斜率,每一點的斜率都不同。如何确定點P0(2,29) 斜率呢?從圖上看,在點P0畫出這個抛物線的切線,切線的斜率就是抛物線的點P0處的斜率。
但如何求切線的斜率呢,因為斜率的定義需要直線上的兩個點來計算,現在隻有P0點而已,微分學給出了繞過這一障礙的方法,那就是間接地逼近這條切線的斜率,這是一條絕妙的進攻路線。
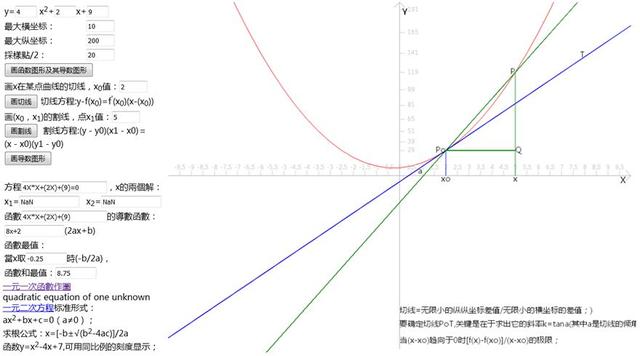
我們需要求出的是曲線在x=2處的斜率,首先我們考慮:選取靠近x=2處的一個點,先選取x=5這一個點P(5,119),兩點PP0連成了一條割線,用割線的斜率來近似點P0的切線的斜率。
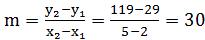
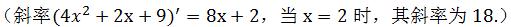
| x | y | 割線斜率 | |
| 5 | 119 | 30 | |
| 4 | 81 | 26 | |
| 3 | 51 | 22 | |
| 2.5 | 39 | 20 | |
| 2.1 | 30.84 | 18.4 | |
| 2.01 | 29.1804 | 18.04 | |
| 2.001 | 29.018 | 18.004 | |
| 2.0001 | 29.0018 | 18.0004 | |
| 2.00001 | 29.00018 | 18.00004 |
有一個顯然的趨勢,選取點越靠近P0點(x=2),對應的割線也旋轉着更加靠近這條切線。
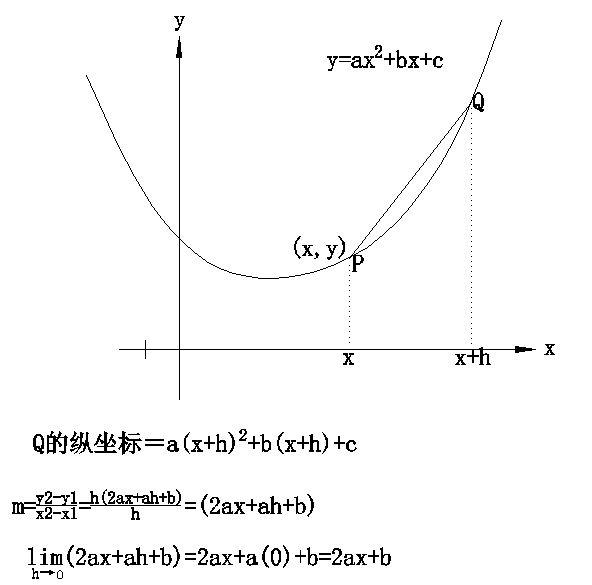
這樣,需要有一個一般的方法去求ax^2 bx c上任意點P0(x0,y0)處的斜率公式:選取一個鄰近點P(x,y),x=x0 h;
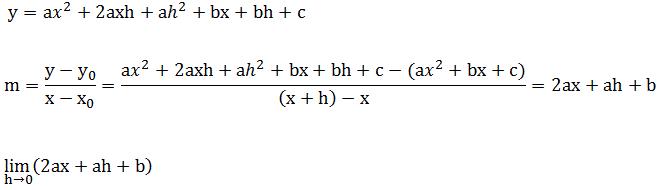
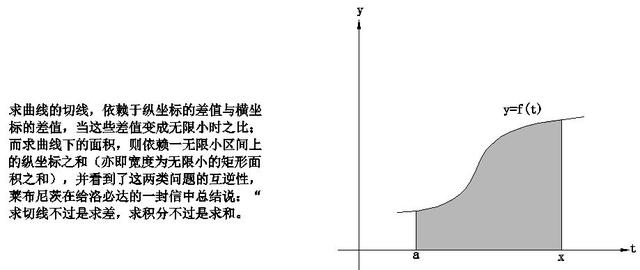
曲線的切線斜率是當h趨近于0時相應割線斜率的極限,這個極限稱為導數,求導數的過程稱為微分。
微分學的目标就是發展更一般的公式。我們肯定不想局限于處理抛物線。使用與上面的過程類似的思路,數學家從一般函數y=f(x)開始,求其上任意點(x,y)處的切線的斜率。同上,我們在這條曲線上選擇一個鄰近點,坐标是(x h,f(x h)),接下來,确定割線的斜率:
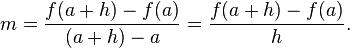
最後求當h→0時,上面這個商的極限值。
萊布尼茨把導數記為:
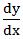
後來約瑟夫﹒路易﹒拉格朗日(1736-1813)引入更強大的記法,使用符号f’(x)表示f(x)的導數。
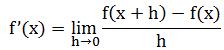
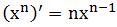
求曲線的極大值和極小值的關鍵是我們前面讨論的斜率,在小山的頂部或狹谷的底部,曲線的切線是水平的,即是一條水平直線,它的斜率是0.用代數的語言表示,求函數的極值,可以轉換為求函數的導數等于0的方程解。
我們可以從一個實例去充分領略微分學的風範。
意大利數學家吉羅拉莫﹒卡爾達諾(1501-1576)有一個論斷:不存在兩個實數(設為x,y)滿足其和等于10且其積等于40;利用微分學,我們很容易證明他的結論。
f(x)=xy=x(10-x)=-x*x 10x,求其極大值。
f’(x)=-2x 10,當x=5時,f’(x)=0,xy=25,和等于10的兩個實數有極大積25.
如果讨論周長為20的幾何體,哪一類及相應參數設計如何達到面積最大?圓,面積可達100/pi.
微分的概念是在解決直與曲的矛盾中産生的,在微小局部可以用直線去挖替代曲線,它的直接應用就是函數的線性化。微分具有雙重意義:它表示一個微小的量,同時又表示一種與求導密切相關的運算。
微分的思路就是一個線性近似的觀念,利用幾何的語言就是在函數曲線的局部,用直線代替曲線,則線性函數總是比較容易計算的,因此就可以把線性函數的數值計算結果作為本來函數的數值近似的值,這就是利用微分方法進行近似計算的基本思想。
函數與其導數是兩個不同的函數,而導數隻是反映函數在一點的局部特征,如果要了解函數在其定義域上的整體特征,就需要在導數和函數之間建立起聯系。微分中值定理(包括羅爾定理、拉格朗日中值定理和柯西定理、泰勒定理)是溝通導數值與函數值的橋梁,是利用導數的局部性質去推斷函數整體性質的工具。
利用中值定理通過導數去研究函數的形态,如判斷函數的上升、下降、極限值、凹形、凸形和拐點等重要形态,從而把握住函數圖像的各種幾何特性。
中值定理刻畫了函數在區間上的增量與函數在敬意内的某一點的導數的關系。
在數學中,微分是對函數在局部變化率的一種線性描述,微分可以近似地描述當函數自變量的取值作足夠小的改變時,函數的值是怎樣改變的。
-3-
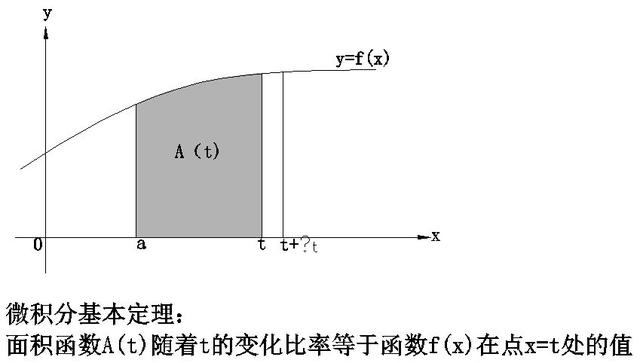
微分學研究的是曲線的斜率,而積分學描述的是曲線下的面積;對于圓和梯形等不同圖形的面積我們需要應用不同的公式,相對而言,積分采用更一般的視點,尋找一個統一的方法求任意函數界定的面積。
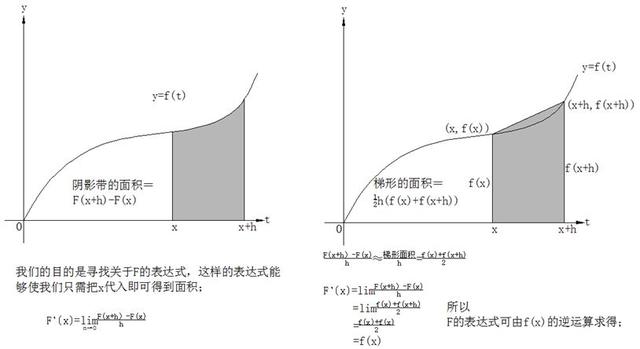
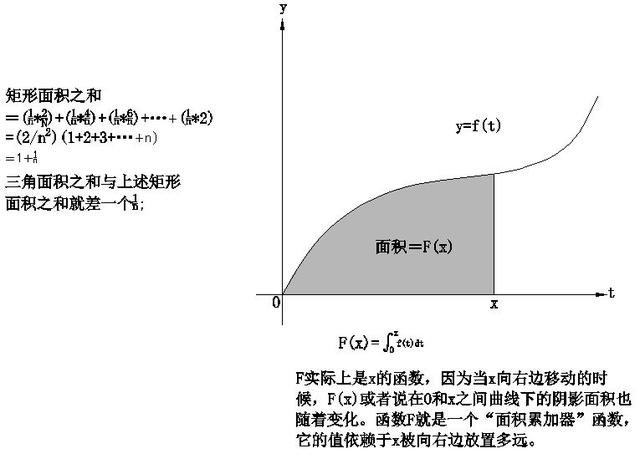
如前面微分學的思路,由割線的斜率去逼近目标點的切線的斜率,曲線下面積的求法的思路也可從矩形的面積累積:構造的矩形的高可由t的值,通過y=f(t)求得,如下圖,曲線下面積≈矩形面積之和= f(t1)△t1 f(t2)△t2 f(t3)△t3.顯然,這個面積隻是粗略地近似。如何改進它呢?合适的技巧就是更多的細分:利用極限的思路,不要止于一千或一百萬個矩形,讓它們的數量沒有限制地增加,甚至到了它們的寬度逼近0.
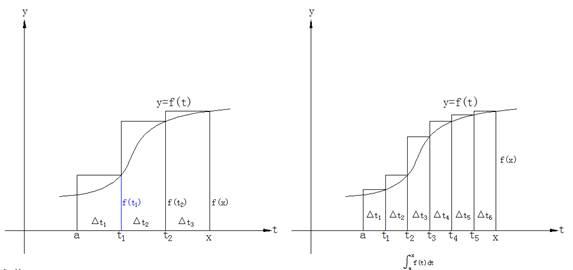
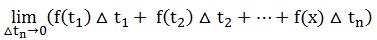
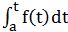
我們可以考慮先從一個最簡單的例子開始,求直線y=f(t)=2t下從t=0到t=1的面積,如下圖所示。它的面積借助三角形的知識,可知面積是1.

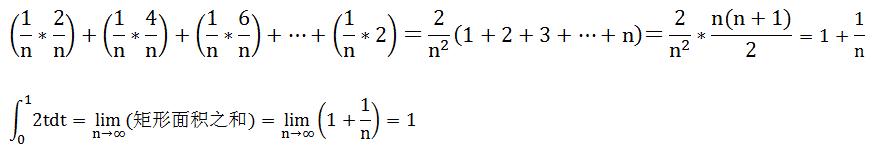
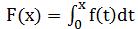
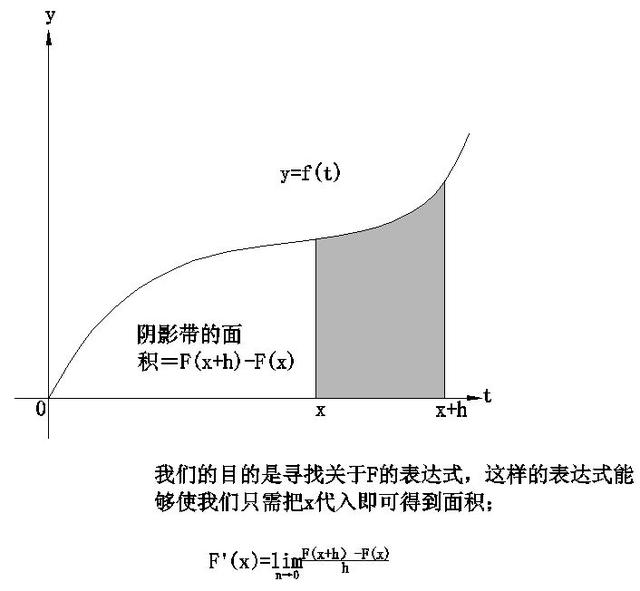
數學家的目标就是要尋求關于F的某類公式,這樣使得我們隻需把x代入到F裡就可以确定這個面積。
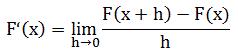
根據F的定義,我們知道F(x h)是由曲線y=f(t)在t=0到t=x h之間所圍成的面積。因此F(x h)-F(x)是它們的面積之差。
我們連接(x,f(x))和(x h,f(x h))兩點,使用梯形面積近似求得不規則帶的面積:1/2h[(f(x) f(x h))],F(x h)-F(x)=不規則帶的面積≈梯形面積=1/2h[f(x) f(x h)]

變上限積分
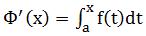
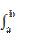
定積分的概念的産生來源于計算平面上曲邊形的面積,解決的基本思路是用有限代替無限。
不定積分的概念是為了解決求導和微分的逆運算而提出的。
-4-
4.1 正方形鐵皮, 邊長為a,截去四角,做成一個無蓋的盒子,怎樣截角可能做到盒子體積最大?

4.2 一張A4紙大小的鐵皮,截去四角,做成一個無蓋的盒子,怎樣截角可能做到盒子容積最大?

4.3 任意長寬的平面w*L

-5-
5.1 求切線不過是求差,求積分不過是求和 ↓

5.3 割線斜率的極限 ↓
5.4 斜率(間接地逼近) ↓
5.5 求導過程 ↓
5.6 牛頓方法 ↓
5.7 基本求導和積分公式 ↓

5.8 面積函數的導數 ↓
5.9 面積函數的導數是原曲線函數(面積近似于梯形) ↓

5.10 面積函數與曲線函數 ↓
5.11 微積分基本定理的啟發式推導 ↓
記得剛參加工作那會,剛好是農村責任田按每家每戶人口數量調整的時候。對責任田的丈量涉及到兩個知識點,一是單位的換算,農村習慣使用的單位是多少畝多少分的田(1畝=10分=666.67平米);二是責任田的形狀确定的問題。
因為大部分田的形狀并不是規整的幾何形狀,對于形狀不規整的田的面積的丈量,其思路也很簡單,就是劃分出若幹小的規整的形狀,對于一些形狀也可以是割多填少的方式,通過測量每個劃分出的小形狀(如方形、梯形等)并彙總這些小形狀的面積即可。自然,劃分得越細,最後求和得出的數據與實際的面積越接近。
The End
,更多精彩资讯请关注tft每日頭條,我们将持续为您更新最新资讯!



