正态分布有什麼意義?正态分布也叫高斯分布，是大家最熟悉的概率分布正态分布概率密度函數大家也都知道，長的很像鐘，所以也叫鐘型曲線那有一個很有意思的問題就是為什麼這條曲線長成這個樣子，今天就給聊聊這個很有意思的話題，下面我們就來聊聊關于正态分布有什麼意義?接下來我們就一起去了解一下吧!

正态分布有什麼意義

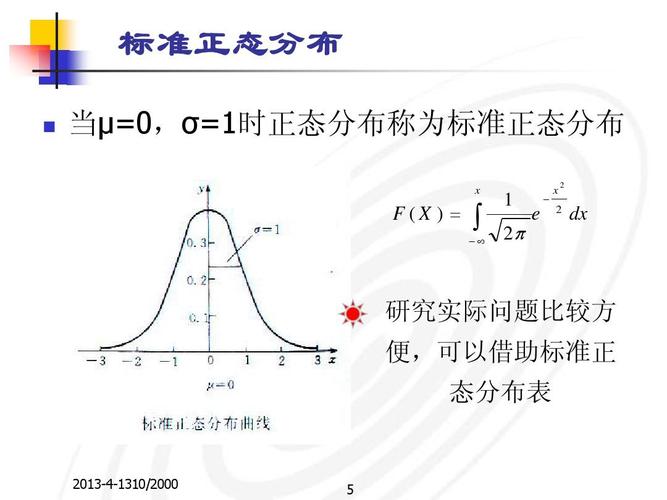
正态分布也叫高斯分布，是大家最熟悉的概率分布。正态分布概率密度函數大家也都知道，長的很像鐘，所以也叫鐘型曲線。那有一個很有意思的問題就是為什麼這條曲線長成這個樣子，今天就給聊聊這個很有意思的話題。

其實正态分布的出現和最小二乘法類似來自對誤差的計算，當然那個時代很多概率統計公式大都來自于對誤差的計算。什麼意思呢？就是說比如我對一個物體長度進行測量，我假設這個物體的長度為1米--事實上我不知道，當然我也不可能知道，這個是永遠都不能測量準确的大家應該都知道--我在多次測量時，會出現以下結果，如：1.01,1.02,1.15,0.99,0.85等等數據。總之在我測量時可能會出現比1大的數據，也會出現比1小的數據。這個我覺得大家都能理解，有誤差，有大有小才對。而且誤差越小則出現的概率越大，或者說誤差小的數值出現的可能性要比誤差大的數值出現的可能性要大。舉個例子，比如你測量出來1.05這個值的概率肯定比你測量出10米(這個值有些誇張)的概率要大，而且誤差在真實值兩側是對稱的。這個對稱的意思是說，你可以測量出一個1.01(比1大0.01)的值當然你就可以測出一個0.99(比1小0.01)；1.01和0.99出現概率是一樣的。也就是說這個誤差在真實值兩側有對稱性。到現在為止出現了兩個原則：1，誤差越大其出現的概率越小；2，誤差在真實值兩側對稱；接下來就是第三點了，這個真實值到底是什麼。或是這個真實值到底該怎麼求呢。高斯給出了一個方法，就是求平均值。這個方法到底對還是不對？其實在今天看來好像是沒有什麼問題，但是在當時提出時，可能就是一片噓聲--wtf。那高斯到底是如何來思考這個問題的呢？或是說高斯是怎麼自圓其說的呢？

其實高斯給出的說法是，我想知道我測量的誤差到底是怎麼樣的，或是我測量的誤差的概率到底是呈現一個怎麼樣的形态，我先假設這個誤差概率分布為f(x)（這也是概率密度函數，因為連續随機變量單個值的概率為0，這裡面讨論的是連續随機變量），假設真實值是θ，而測量值為X1，X2，X3.....Xn，那麼我假設有這個函數

L（θ；X1，X2，X3.....Xn）=f(θ-X1)*f(θ-X2)*f(θ-X3)...f(θ-Xn),我想找到一個θ，使得這個函數L的值最大。當L達到最大後的θ就可以作為我們想要的真實值的估計了(或是就作為真實值了)。那麼為什麼要使得L的值最大呢？上文已經提到了，你測量時，不管真實值是多少，你距離真實值越近這個值出現的概率就越大。所以你如果每一個值都靠近真實值，則測量的越準确。可是問題依然解決不了，f(x)是什麼呢？θ也不知道。盡管讓L取最大值沒有問題，可是問題依然解決不了。高斯這個時候就将平均值(X1 X2 X3..... Xn/n)作為θ的真實值，然後來求f(x).最終得出的結論是f(x)是正态分布也就是那個鐘型曲線。能服衆否？其實勉強可以服衆，因為平均值自古以來就是一個很好的求真實值的方式，這樣正态分布就出來了

但是終究有很多讓人覺得别扭的地方：就是算數平均是個好的方式，所以誤差要服從正态分布；而用了這個正太分布以後你在誤差最小可以推導出最小二乘法很好用(平均值就是最小二乘法一個特殊形式)。結果怎麼說都是正确的。不過後來拉普拉斯用了他的中心極限定理給這個正太分布進一步的加注了一下。在這裡要先說一下，拉普拉斯的中心極限定理出現的時間要比正态分布要早。

是不是可以這麼理解一組數和他平均數之間呈現着這麼一種關系，這種關系就是正态分布？

本文參考了：陳希孺數理統計簡史

更多精彩资讯请关注tft每日頭條，我们将持续为您更新最新资讯!