訓練2重點依舊是球體問題和最值問題，難度定位為中上難度。

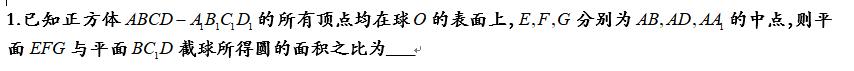
截面圓的面積比取決于截面圓半徑的比值，而球體内截面圓的半徑的平方可用球體半徑的平方減去球心到圓心距離的平方得到，因此計算出球心到兩個截面圓心的距離即可，因為三角形EFG和三角形BC1D均為等邊三角形，所以球心到截面圓心的距離就等于球心到兩個面的距離，求距離時可建系來解，也可用三元一次方程表示出平面的方程，利用點到平面距離公式也可。

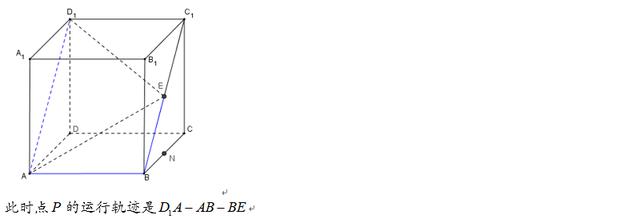
截面問題不是高中立體幾何中的常見問題，很多同學也比較容易忽視，但是在2018年高考中第12題的位置曾經出現過以截面形式的最值問題，在本題目中是以向量的形式出現，D1,P,E,F四點不一定共線，但一定共面，而不共線的三點構成一個平面，因此隻需要考慮D1,E,F三點構成的平面即可，由于點F是AD上的動點，F點的變化會影響截面的變化，因此可通過特殊位置确定出點F在A,D兩點處的截面，從而确定出截面變化的區域。

這裡需要糾正一個很容易誤判的結論，在正四面體中側面和底面所形成的二面角并不是60°，而是一個比60°大的銳角，題目沒什麼難度，需要注意為什麼有兩個取值。

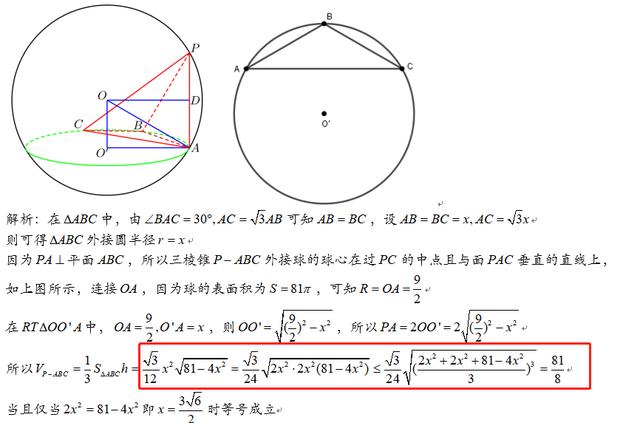
這種題目是高考中常見的題目，有的題目是底面确定，高不确定，讓求體積的最值，有的是高确定但底面不确定，在本題目中底面是一個确定的形狀，但邊長并不确定，可通過設底面三角形中某個邊長為x，用x表示出高的值即可，還是需要先根據兩個特殊面确定出球心的位置，表示出體積後不要貿然換元，可通過變形轉化為均值不等式的擴展形式求最值即可。

題目給的條件并不完整，但根據特殊性屬于一般性的原則，可把題目中描述的幾何體看作是一個正四棱錐，注意并不是所有棱都相等，另外即便所有棱都相等，側面和底面形成的二面角也不是60°，設點用兩個法向量即可求出二面角的餘弦值。

本題目是一個非常有意思的題目，由于截面具有随意性，讓求截面所形成的直角三角形斜邊的最小值，需要将斜邊表示出來，但直角邊并不能直接表示出來，加之題目中給定的是直三棱柱，可通過在側面上構造直角三角形來表示出三邊，進而找到滿足斜邊最小時的條件。

下面是某位同學問到的兩個題目：

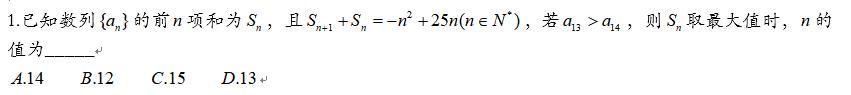
這種題目在初學等差數列中經常遇到，例如遞增且首項為負的等差數列，n取何值時和有最小值，這種題目的做法有兩種，第一種直接表示出等差數列的前n項和的式子，利用二次函數的最值來做，要麼找到等差數列正負分界時的n值即可，在本題中也是如此，先判斷出數列是遞減的等差數列，找到正負分界時的n即可。

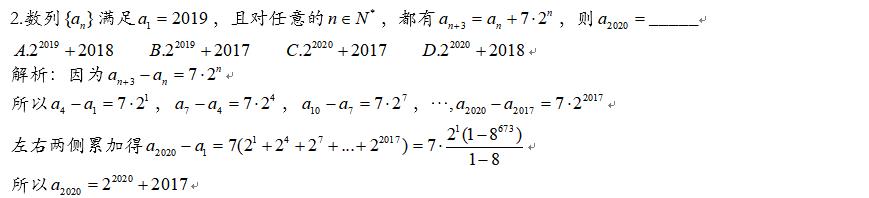
本題目是類似于遞推公式中的累加法，但是并不是前後兩項相減的形式，所以不可按照常規的從n=1,2,3...這樣寫，中間會有幾項消不掉，所以應該按照n=1,4,7,10...的形式寫，這種題目無論是中間差幾項都是如此，前後相鄰隻是一種特殊情況，要學會分析和舉一反三。

更多精彩资讯请关注tft每日頭條，我们将持续为您更新最新资讯!