一、前言

• 背景：ABTester實驗是具有一定前瞻性，統計性，科學性的特點。用好了就實現了在大數據時代的充分利用數據分析問題，解決問題，為決策提供強有力的依據，但是有時候用戶在使用ABTester時候，會出現一些痛點和疑惑。
• 痛點：
• 每次實驗需要多少流量
• 實驗時間開多長沒有概念
• 解決問題：
• 為了驗證某一個功能特性，一個實驗需要開多少流量。
• 一個實驗需要開多長時間

二、基礎概念1、研究對象總體X：研究問題某個數量指标。2、入手點個體：總體中的一個元素xi 樣本：一部分個體Xi3、工具--統計量

4、抽樣分布

• 标準正态分布N(0, 1)
• Ka方分布
• t-分布
• F-分布

5、抽樣定理簡單介紹幾個

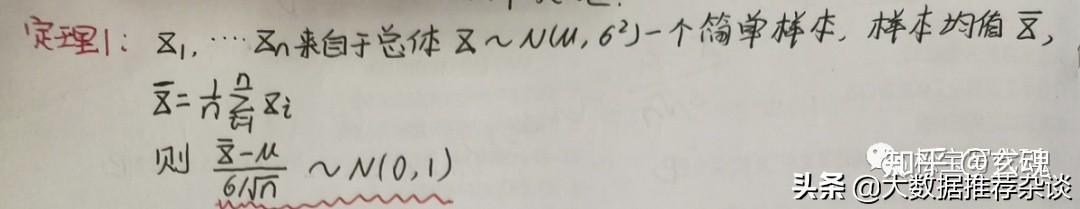
6、參數估計通俗的說：樣本參數去估計總體的參數。舉個 ：

• 樣本均值估計總體均值，
• 用樣本比例去估計總體比例，
• 用樣本方差估計總體方差

（1）分類：點估計和區間估計

• 點估計通俗的說：用樣本的統計量的值直接作為總體參數的估計值。
• 區間估計通俗的說：在點估計的基礎上，給出總體參數估計的一個區間範圍。

（2）置信區間和置信水平 通俗的說：區間估計中，樣本統計量構造的總體參數的估計區間，稱為置信區間。舉個 ：

• 100個樣本，每一個樣本構造一個置信區間，100個樣本構造的總體參數的100個置信區間中，有95%的區間包含了總體參數的真值，5%則沒有包含。

大樣本下，樣本均值的置信區間：

（3）總體均值的區間估計原理 大樣本下，根據中心極限定理，可以得到的樣本均值的抽樣分布。

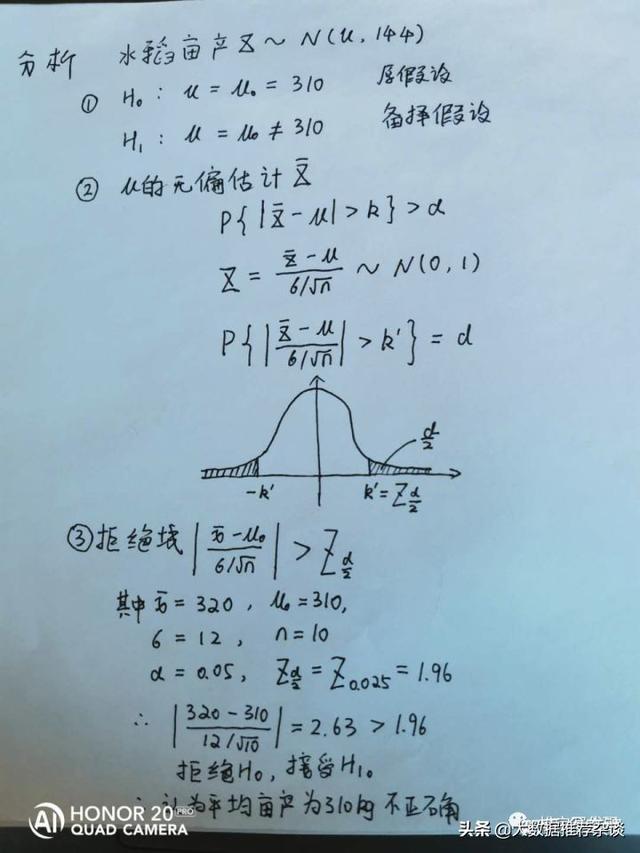
7、假設檢驗我們來看一下一個簡單的假設性檢驗的例子：根據水稻長勢，估計平均畝産310kg，收割時，抽取10塊地，測平均畝産320kg，如水稻産量服從正态分布N(u, 144)，問所估計平均畝産是否正确？（a = 0.05，Z0.05 = 1.645，Z0.025 = 1.96） 分析：當方差已經的情況下，使用Z檢驗；未知的時候，使用t檢驗

三、一個簡單并完整的ABTester例子1、背景和設置

• 背景：有個web應用，接入了咱們sdk，上報各種事件埋點。
• 确認優化的目标：注冊流程改版，從而提供注冊轉換率。
• 注冊流程的A/B測試：之前是使用了圖片校驗碼的方式，但是注冊轉化率偏低。提出設想：圖片校驗碼方式改成短信校驗碼方式，是因為降低了用戶輸入的難度從而可以提高注冊轉換率。
• 我們設置
• 核心指标：注冊轉化率
• 設置版本：1個對照版本（圖片校驗碼）。1個實驗版本（短信驗證碼）。
• 設置版本流量：總流量我們設置50%，各個版本均勻分配。
• web應用引入我們客戶端分流sdk的，然後将版本代碼插入到項目中。

2、結果分析分别為兩個版本分配了25%的用戶流量，通過2個自然周左右的實驗觀察，數據顯示。結果：新版本（短信校驗碼）的注冊轉化率提升了接近10%，并且95%置信區間是[8%, 12%]， 分析：說明這個實驗版本推廣到全量用戶之後，95%的概率下至少會有8%到12%的提升。決策：基于這個實驗結果，産品經理選擇将新版本注冊流程推送給全部用戶，顯著提升了注冊轉化率。四、詳細介紹樣本量計算1、注冊流程改版例子實驗運行後，用戶開始進組。1天後數據統計

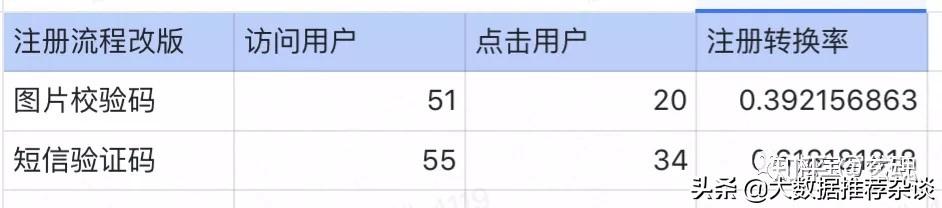
這就能說明：短信驗證碼的功能有效提高注冊轉換率？2天後數據統計

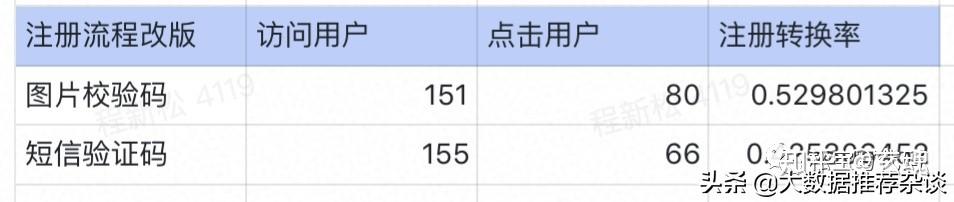
這就能說明：圖片驗證碼的功能有效提高注冊轉換率？那麼到底，注冊流程改版對于提高注冊轉換率是否有顯著性提高呢？暫時是不能給出結論的，因為數據樣本還不夠大，不能充分說明。理論上：樣本量越多越好。現實上：1、自身樣本不夠大；2、試錯成本大。選擇樣本數量是個技術活：樣本量太小，有人罵娘；樣本量太大，還是有人罵娘。那麼問題來了：如何确定一個“最小”的樣本數量，在保證實驗“可靠性”的同時，不會浪費過多流量？2、最小樣本公式統計學裡有最小樣本量計算的公式：

說明：1、n是每組所需樣本量，因為A/B測試一般至少2組，所以實驗所需樣本量為2n；2、α和β分别稱為第一類錯誤概率和第二類錯誤概率，一般分别取0.05和0.2；3、Z為正态分布的分位數函數；4、Δ為兩組數值的差異，如注冊轉換率50%到60%，那麼Δ就是10%；5、σ為标準差，是數值波動性的衡量，σ越大表示數值波動越厲害。從而可知：實驗兩組數值差異Δ越大或者數值波動性σ越小，所需要的樣本量就越小。3、方法一：假設兩個轉換率方差相等條件：假設兩個轉換率的方差（可變性）相等。上面公式轉換為：

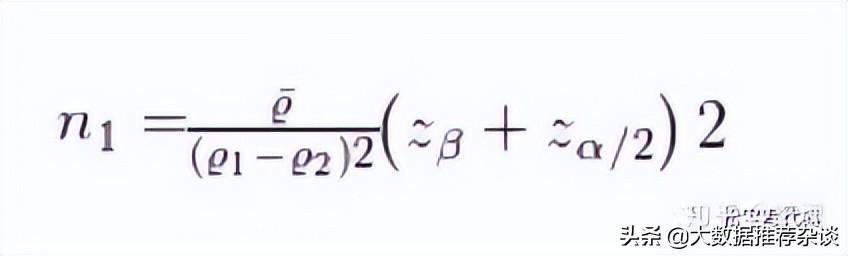
說明：1、e1和e2是真實的注冊轉換率。2、e 是合并方差估計量。3、α是顯著性水平（通常α = 0.05） 4、β是期望功效（通常β = 0.8） 5、Zβ和Zα/2針對給定參數的臨界值α和β 固定值：α = 0.05時，Zα/2 = 1.96。β = 0.8時，Zβ = 0.84。【注冊流程改版例子 】具體計算過程：（1）兩個版本權重相等的情況 這裡使用合并估計量作為方差。

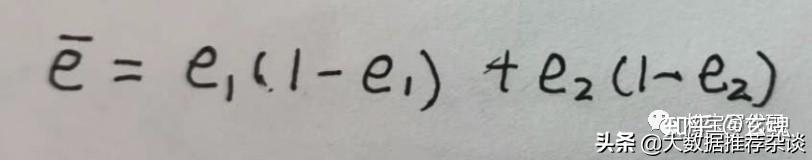
如果我們不假設兩個轉換率的方差相等，則公式會略有不同，後邊給出代入公式，得到最終的樣本的公式：

我們來真實計算一下：1、注冊轉換率e1為50%，e2為60% 2、假設最小标準值為0.8的期望功效 3、顯著性水平α為0.05

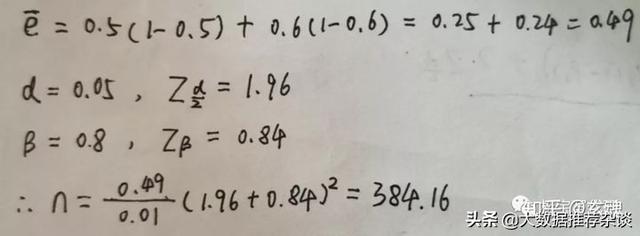
因此。每組（對照組和實驗組）的最小樣本量為385。（2）兩個版本的注冊轉換率權重不等的情況 這種情況下，第一步，假設各組大小相等，計算總樣本量；然後，可以根據兩組實際比率k來調整此總樣本量大小N，而修改後的總樣本大小N '，可以通過下面公式來計算：

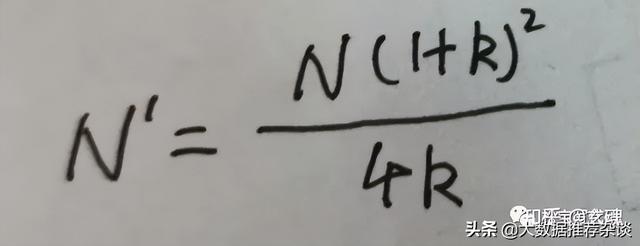
以上兩組中，每個樣本的樣本大小分别為N '/（1 k）和kN '/（1 k）。4、方法二：使用假設性檢驗适用範圍：

• 假設性檢驗本身可以對單個總體參數或者兩個總體參數進行。
• 假設的内容可以是雙側檢驗。比如參數是否等于某個值，還可以參數是否大于或者小于某個值。

AB實驗背景下，我們通常使用的是雙總體雙側檢驗。具體實施 原假設：μ1=μ2 備擇假設：μ1≠μ2構造統計量 條件：兩個樣本間 相互獨立 且樣本量大 我們實際進行兩總體均值差是否為0的雙側檢驗

實際計算中，總體方差可以用樣本方差代替，原假設的背景下u1 - u2 = 0，所以計算統計量z，所需要的數據都可以依據樣本得到。還有假設兩組的總體方差相等的情況，實際上，AB實驗中并不常見。上圖是概率密度曲線：

• 黃色是AA實驗的均值差的分布，藍色是AB實驗（以指标提升為例）的均值差的分布。
• 兩個紅箭頭分别标識 -1.96*指标标準差 1.96指标标準差
• power 即 藍色曲線在紅色（右）箭頭右側的面積。
• delta是上圖 藍色的中軸位置，即 AB實驗（以指标提升為例）的均值差的期望。

得出power的計算公式 power = 1 - norm.cdf( norm.ppf(1 - α / 2) - np.sqrt( sampleperversion * (delta * 2) / 2 * ( metric_variance * 2 ) ) )其中：cdf 累積分布函數，是概率密度函數的積分，能完整描述一個實随機變量X的概率分布。ppf 分位點函數 metric_variance 指标方差 delta 均值的差反推出樣本量

sampleperversion = 2 * (norm.ppf(1 - α / 2) - norm.ppf(β)) * 2 * metric_variance / (delta * 2)

其中：ppf 分位點函數 norm.ppf正态分布的累計分布函數的逆函數，即下分位點。

alpha 默認5%，其中norm.ppf(1 - α / 2) = 1.96，norm.ppf(β)為映射值。

metric_variance 指标方差。

delta 均值的差。

更多精彩资讯请关注tft每日頭條，我们将持续为您更新最新资讯!