（撰文：小留洋•Yvonne）

IMO，International Mathematical Olympiad，國際奧林匹克數學競賽是數學競賽賽道上最璀璨的明珠了，是最高競賽獎項。

但它也不是我們高攀不起的，有些題隻要認真琢磨，就能發現解謎線索，在這過程中你會感覺到自己像柯南，像福爾摩斯，像偵探️‍♀️在探案，那種揭秘的樂趣隻有體驗了才知道有多爽。

來道考古題，1959年IMO第二天第4題。

Construct a right triangle with a given hypotenuse c such that the median drawn to the hypotenuse is the geometric mean of the two legs of the triangle.

用給定的斜邊c構造一個直角三角形，使得到斜邊的中線長度是三角形兩條邊邊長的幾何平均值。

給定斜邊做一個直角三角形，要畫一條從頂點到斜邊的中線，還要知道幾何平均值。回想一下腦子裡的基礎知識。①圓的直徑對應的圓周角是直角，放一邊備用；②取一邊中點，連接對側的頂點就是中線，也不難，等會兒畫；③幾何平均值就是2個數的乘積開平方。

根據已有信息，我們先把斜邊c畫上，考慮直角三角形的那個直角頂點可能在什麼地方。觀察下圖。紅色C點在圓上，△ABC一定是直角三角形。

再把到斜邊c的中線畫出來，以便觀察。

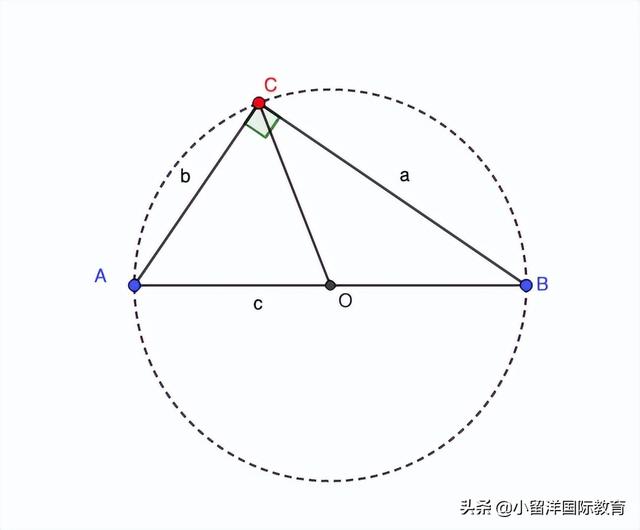
還不足以确定C點的具體位置，繼續探索。

還有一個關鍵信息沒用上，中線長度是a和b兩個直角邊的幾何平均值。CO=√(a•b). 我們列公式觀察幾個變量的關系。中線CO也是半徑，c是直徑，所以CO=c/2。根據勾股定理，a² b²=c²。

代換變形都用上，看看能得到什麼有用信息。

有點意思了，也就是說，隻要能構造出一個c線段√3/2倍長的線段，我們就構造出了a b，就是相當于把a和b兩條線段拼接在一起了。

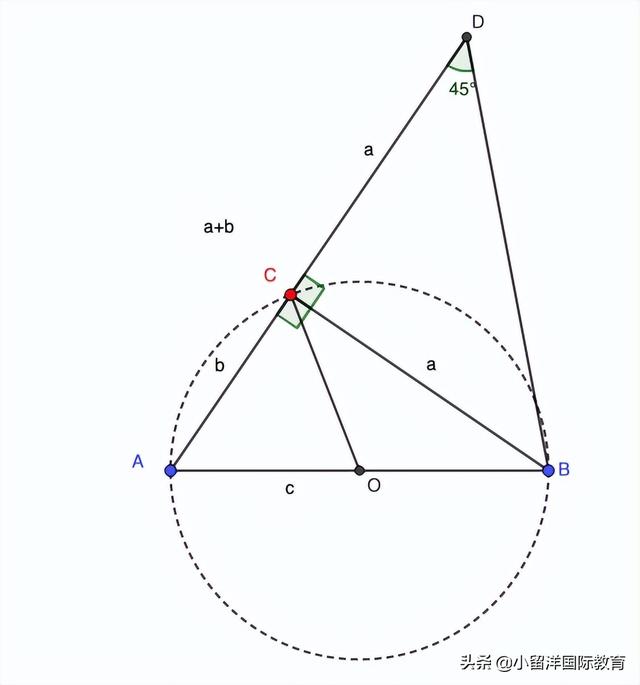
我們再從預期的結論往前推看看有什麼線索。看上圖，假定圖已經做出來了，将AC延長至D，CD長度等于a，那麼AD就是a b，可知，CDB是等腰直角三角形，∠D是45°。

好像差不多了，如果AD也就是a b這條線段已經得到，線段c也是已知的，我們在D點做一個45度角，以A為圓心c為半徑做圓，與45度角的射線交于B，再從B做一條垂線垂直于AD，垂足是C，這樣三角形ABC就得到了。

至于如何得到√3/2c長的線段，我們下面有個圖，大家自己琢磨一下，我們在講做鹦鹉螺曲線的文章裡講過。

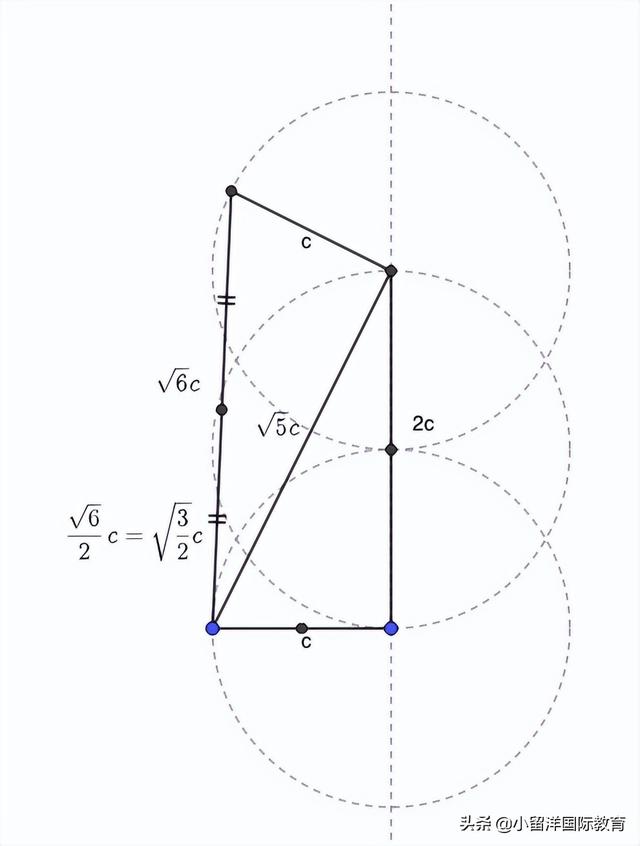
繪制a b線段，也就是√(3/2)c長度的線段。

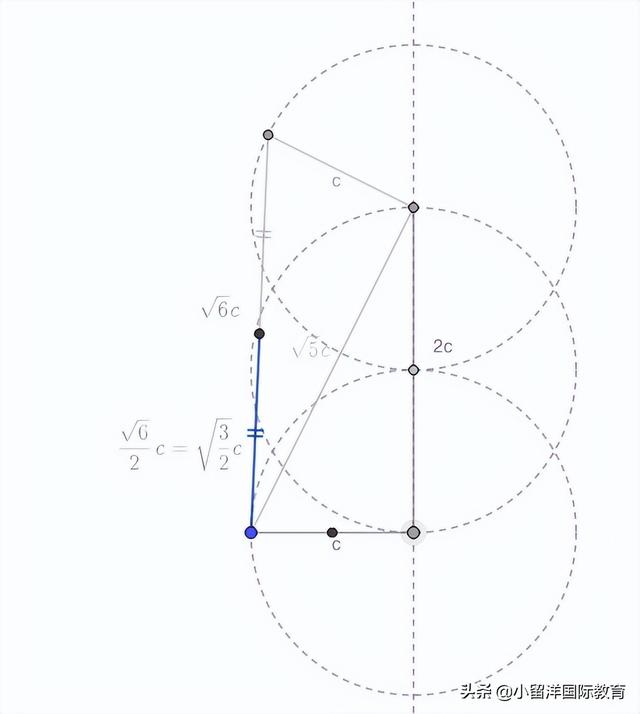
以D為頂點做45度角，做射線。

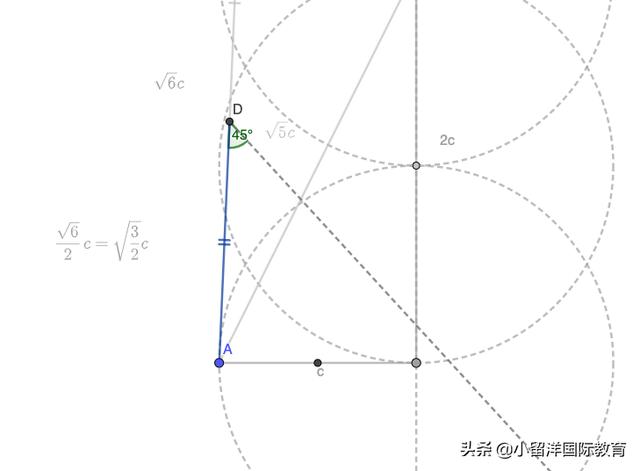
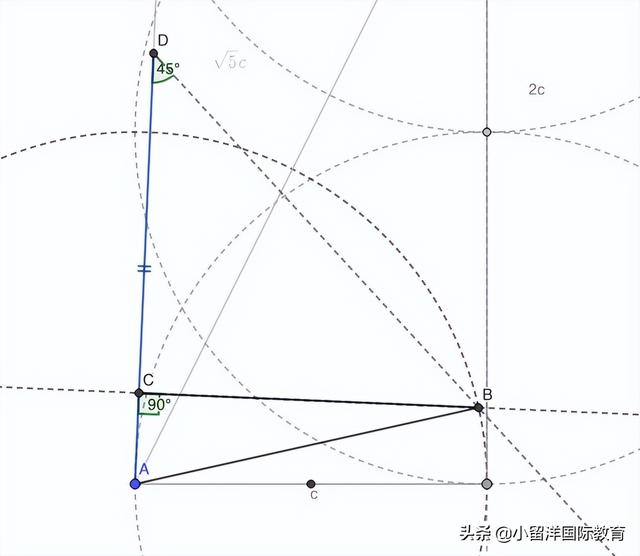
以A為圓心，c為半徑做圓，交射線于B。

過B點做AD的垂線，垂足是C點，連接ABC，完成作圖。

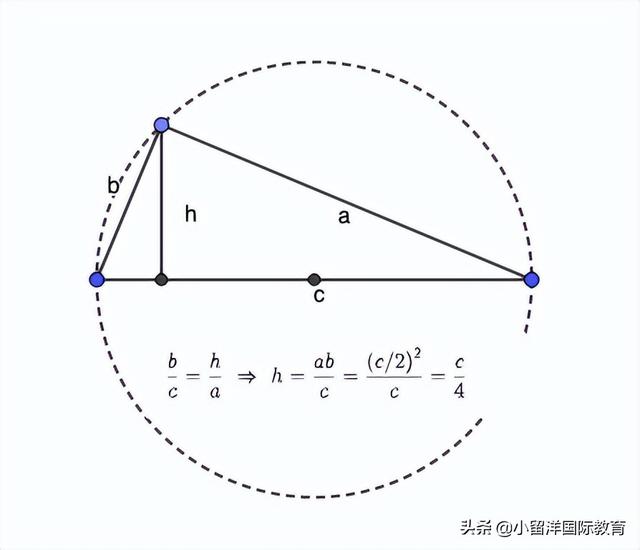
還有沒有其他方法？做三角形的高h觀察。利用相似三角形做變化，得到高h為c/4。知道高，C點又在圓上，作圖可以更簡單。

做c/4線段

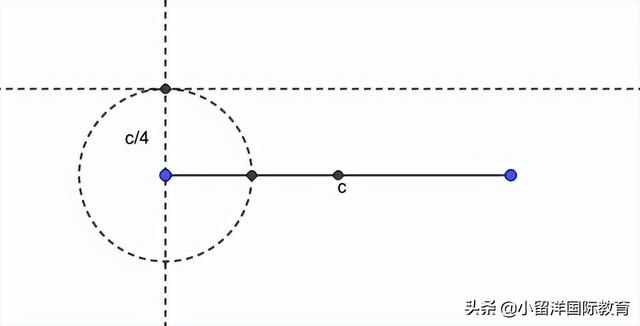
做斜邊c的平行線，距離c/4

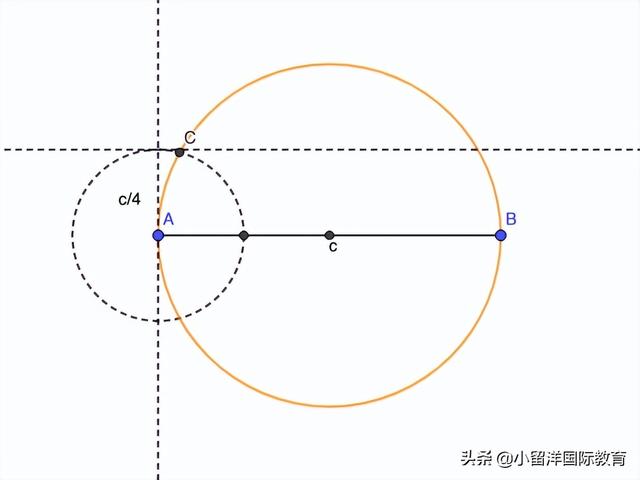
以斜邊c為直徑做圓，交平行線于點C

連接ABC，作圖完成。

☎ 關注「小留洋」，獲取更多海外K12教育資料。

更多精彩资讯请关注tft每日頭條，我们将持续为您更新最新资讯!