整體思想是一種重要的數學思想,它抓住了數學問題的本質,是直接思維和邏輯思維的和諧統一.有些數學問題在解題過程中,如果按照常規解法運算較繁,而且容易出錯;如果我們從整體的高度觀察、分析問題的整體形式、整體結構、整體與局部之間的關系、聯想相關的知識,就能尋求捷徑,從而準确、合理地解題. 這種思想方法在解題中往往能起到意想不到的效果．學生如果能應用整體思想思考問題，不僅有助于學生找到鋸決問題的便捷方法，而且有助于鍛煉學生的思維，提高學生解決實際問題的能力．

類型1、整體思想在求值題中的應用

在代數中有一類題目，給出一個含有未知變量的等式，而該等式的分解因式不能輕易看出，甚至根本沒有辦法在整式範圍内分解，這為解出未知變量增加了難度，此類問題用最常規的思維方法來解，必然要先求出未知變量，然後代進所求的式子中進行求解．這種常規方法雖然可以求出答案，但是過程繁瑣，計算複雜．而用整體法求解則會截然不同．

【點評】此題考查了代數式求值，利用了整體代入的思想，熟練掌握運算法則是解本題的關鍵．

【點悟】 本題簡捷求解的關鍵是充分利用根與系數的關系和根的概念得出m n=1,mn=-3,n2=n 3,整體代入所求代數式求值.

類型2、整體思想在解方程中的應用

整體思想在解方程中的應用，主要表現在整體換元法，整體換元法主要是指在方程中未知數不易求的時候，将式子的一部分用另一個未知數來代替，解出所設的未知數．

【點評】本題考查了換元法解一元二次方程．把一些形式複雜的方程通過換元的方法變成一元二次方程，從而達到降次的目的．

類型3、整體思想在求解陰影部分面積中的應用

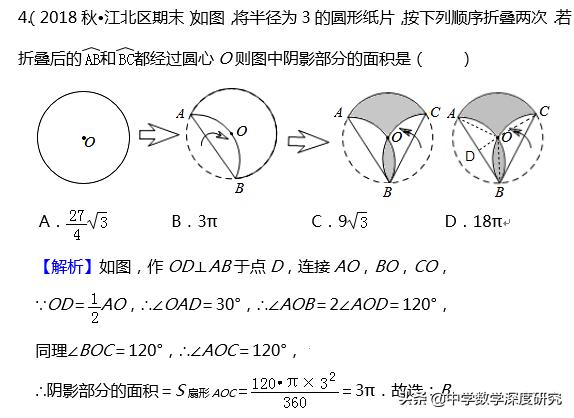
【點悟】 (1)本題的求解着眼于整體,把不規則圖形的面積整體把握,化為規則圖形的面積的和或差,站在一定的高度上求解,給人以大氣、豪邁的感覺.

(2)求解圖中的陰影部分的面積的方法很多:求差法、分割法、割補法、等積法、整體法、特殊法、直接法等.

類型4、整體思想在解應用題中的應用

整體思想在解答應用題中的應用，難點在于能夠抛開細枝末節，放眼整個題目，然後從題目的整體意思去體會所求未知量與已知量之間的關系，并能夠摒棄題目中的幹擾數據，抓住題目的本質，從而避免走彎路，直接求出未知量．

5.小明和小麗家相距1.8千米，有一天小明與小麗同時從各自家裡出發，向對方家走去，小明家的狗和小明一起出發，小狗先跑去和小麗相遇，又立刻回頭跑向小明，相遇後又立刻跑向小麗……如此小狗一直在小明與小麗之間跑動．已知小明的速度是50米/分，小麗的速度是40米/分，小明家的狗的速度為150米/分，當小明與小麗相遇時，小狗一共跑了______ 米．

分析： 通過分析很容易想到，要求小狗一共跑的距離，就必須知道每次小狗遇到兩人時，走的各段的路程，然後将這些段的路程加起來即為一共行走的距離，此種方法解題是因為在小明往返的過程中多次碰見小明和小麗，如果一次次地計算路程，必然因為次數較多，思路稍有疏忽就很容易将總路程計算錯誤．而用整體思想，無需考慮繁瑣的過程，隻需要知道路程等于時間與速度的乘積，又速度已知，時間即為小明和小麗相遇所用時間，解題思路清晰，方法巧妙，且不易出現計算上的問題．

【解答】設經過x分鐘兩人相遇，依題意，得：（50 40）x＝1800，

解得：x＝20，∴小狗跑的路程為150×20＝3000（米）．故答案為：3000．

更多精彩资讯请关注tft每日頭條，我们将持续为您更新最新资讯!