在我們解決數學問題時，經常遇到探索規律或者方案确定問題。這是一類非常重要的問題，無論是在平時考試中還是在數學競賽中，都是一個重點内容。它涉及到統籌法的應用、容斥原理和歸納的數學思想方法，本篇文章就分類來講解這類問題的思路和方法：
一、核心知識1．統籌法的應用——生活中會遇到這樣一些問題：完成一件事怎樣合理安排，才能做到所用的時間最少；把一批貨物從一個地方運到另一個地方去，選擇什麼樣的運輸方案，才能運費最省；車站設在什麼地方，才最方便附近工作的乘客等．此類問題都涉及到如何統籌，目标是選擇最佳．
2．容斥原理的應用：
（1）數集：把若幹個數聚在一起叫數的集合，簡稱數集．例如0，1，2三個數，可寫成集合{0，1，2}，其中0，1，2叫做這個集合的元素，一般集合用A、B、C等表示，用a、b、c等表示集合的元素，用|A|、|B|分别表示集合A、B元素的個數，用A∩B表示A和B的公共部分（即交集），用A∪B表示A或B的部分（即并集）．
如設集合A={0,1,2,3,4}，B={2,3,4,5}，則|A|=5，|B|=4，A∩B={2,3,4}，A∪B={0,1,2,3,4,5}．
（2）容斥原理公式：
3．歸納思維——通過特例的觀察、實驗、抽象概括，引起直覺上的共鳴，發現事物的共性，這種規律性的思維過程稱為歸納思維（即不完全歸納法）．
二、例題講解（一）統籌法的初步應用【點拔】關注分析等待修理時間長的機床數的多少，哪一種更有利？
【解答】7x5 8x4 10x3 15x2 29x1=156(分鐘）
156x5=780（元）
【反思與小結】一般地，哪一個修理的時間最短，下修理哪一個.從整體上來說，先修理用時最短的，其他等待的總時間最短，從整體的經濟效益來說，損失最小。
【點拔】思考哪些事情是必須的，哪些事情可以同時做？從整體上統籌．
【解答】解：開水壺2分鐘→燒開水15分鐘（洗熱水瓶1分鐘，洗茶杯3分鐘，拿茶葉2分鐘）→沏茶，所以最少需要17分鐘．
【反思與小結】要從整體統籌，清洗水壺、燒水是必須的，而其他的事情可以在燒水的時間去做，因此要從整體上思考才能做到所用的時間最短。
【點拔】要使時間最短，必須每次同時烤兩面，怎樣做到每次同時烤兩面呢？
【解答】最少需要9分鐘
（二）容斥原理的應用【點拔】注意弄清題意，搞清此題是求哪些集合的公共部分，然後根據容斥原理解決．
【解答】設三種外語都懂的為x人，則91=47 50 50-22-21-23 x, 所以x=10
既三種外語都懂的有10人
【反思與小結】解決此類問題，通常利用“韋恩圖”的方法來解決。如左圖。
其中A、B、C分别表示具有A、B、C三種性質的集合，而A、B的公共部分表示
具有A、B兩種性質的集合，A、B、C的公共部分具有A、B、C三種性質的集合。
【點拔】關注找到能被4整除的數、被6整除的數分别有幾個，既能被4整除的數又能被6整除的數有多少個。
【解答】解：設A={1000-2000能被4整除的數}，B={1000-2000能被6整除的數}
則需要計算的是|A∪B|
能被4整除的數第一個是1000，最後一個是2000，則|A|=（2000-1000）/4 1=251
能被6整除的數第一個是1002，最後一個是1998，則|B|=(1998-1002)/6 1=167
A∪B={1000—2000既能被4整除又能被6整除的數}={1000—2000能被12整除的數}
因為能被12整除的數第一個是1008，最後一個是1992，則
| A∩B |=(1992-1008)/12 1=83
所以| A∪B |=|A| |B|-|A∩B|=251 167-83=335
即在1000—2000之間，包括1000和2000，能被4或6整除的數有335個
【反思與小結】運用容斥原理解決有關問題，一定要搞清楚每個集合的對象，以及集合中元素的個數，尤其關注相關集合之間的公共部分、并集部分的元素以及數目不要搞錯。
（三）歸納思維問題一：a、b為兩個正整數，且滿足a b=10，探究ab的值？
猜想：當a=________，b=________時，ab的值最大，最大是______________；
問題二：a、b為兩個正數，且滿足a b=10，
猜想：當a=________，b=________時，ab的值最大，最大是______________；
簡要說明：設a=5 x，則b=________，則ab=________，
此時當x=________時，ab最大，最大是_____________；
圖形說明：觀察圖形，分别用兩種方法表示陰影部分的面積：
第一種：______________________________；第二種：______________________________；
得到關于a、b的公式是：______________________________；
觀察下列發現當a、b接近時，陰影部分的會越來越_______________；
猜想：當ab、滿足_________關系時，ab的值最大，最大是_______；此時陰影部分的面積為_______；
問題三：a、b為兩個正數，且滿足a b=m，其中是固定的正數，
猜想：當a=________，b=________時，ab的值最大，最大是______________；
問題四：a、bc、為三個正數，且滿足a b c=m，其中是固定的正數，
猜想：當a=________，b=________，c=________，時，abc的值最大，最大是______________；
【反思與小結】利用歸納方法探究問題一般遵循“特殊——一般——特殊”的規律。從特殊的數字、位置研究某一問題，歸納出具有一般意義的結論，再在特殊數字、位置中驗證所得到的結論正、誤。本例利用歸納得出兩個正數的和是一個定值，當兩個正數相等時，乘積最大。
（1）如圖1，延長△ABC的邊BC到點D，使CD=BC，連結DA．若△ACD的面積為S1，
則S1=______（用含a的代數式表示）；
（2）如圖2，延長△ABC的邊BC到點D，延長邊CA到點E，使CD=BC，AE=CA，連結DE．若△DEC的面積為S2，則S2=__________（用含a的代數式表示）；
（3）在圖2的基礎上延長AB到點F，使BF=AB，連結FD，FE，得到△DEF
（如圖3）．若陰影部分的面積為S3，則S3=__________（用含a的代數式表示），
并運用上述（2）的結論寫出理由．
發現：像上面那樣，将△ABC各邊均順次延長一倍，連結所得端點，得到△DEF（如圖3），此時，我們稱△ABC向外擴展了一次．可以發現，擴展一次後得到的△DEF的面積是原來△ABC面積的多少 倍．
應用：去年在面積為的△ABC空地上栽種了某種花卉．今年準備擴大種植規模，把向外進行兩次擴展，第一次由△ABC擴展成△DEF，第二次由△DEF擴展成△GHI（如圖4）．求這兩次擴展的區域面積共為多少？
【反思與小結】三角形之間的面積關系，可以通過比較兩個三角形的底、比較它們的高發現兩者之間的關系.
④=_________；⑤=_________；……
則第個等式是：______________________________；能否證明第個等式？
【點撥】觀察每個等式的結果與四個因數中哪些因數有關？能否歸納其規律？
對于等式的正确性需要利用多項式乘法進行證明，證明時，能否根據從等式右邊的結果出發，思考左邊利用乘法結合律與“整體”的數學思想進行證明？
【點撥】能否通過第一次操作、第二次操作、第三次操作尋找規律，進行解答？
【反思與小結】本題體現了一般與特殊的數學思想，首先對于比較複雜的數字問題，通過用字母表示數，發現其中的規律，這是由特殊到一般的過渡，在數學上稱為一般化的方法；由一般化的方法所得到的規律，可以進行實際的應用，解決具體的問題，這是一種由一般到特殊的過渡，在數學上稱為特殊化的方法.
【點拔】能否找到使f(n)不是質數的的值？
【反思與小結】從特例中悟出規律，也就是從具體實例的個性悟出個性中所隐含的共性（規律性的東西）的思維是一種不完全歸納，隻能是合情推理，其結論可能是正确的，也可能是錯誤的，隻有通過邏輯證明（以後還要學習），才能确立猜想的正确性．所以對歸納思維應保持積極的态度，既要大膽猜想發現的規律，又要小心求證。
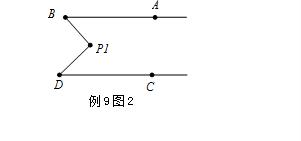
（2）在圖2中，如果AB∥CD，探究∠ABP1、∠CDP1、∠BP1D的之間的數量關系，并說明理由；
（3）在圖3中，如果AB∥CD，探究∠ABP1、∠BP1P2、∠CDP2、∠P1P2D的之間的數量關系，并說明理由；
（4）在圖4中，如果AB∥CD，探究∠ABP1、∠BP1P2、∠CDP2、∠P1P2D的之間的數量關系，并說明理由；
容斥原理是數學競賽的四大原理之一，在初中競賽中多有涉及，是計數方法必不可少的知識。就是有重疊計數的就減去，有少計數的就加上，在平時習題中大家注意多加練習。而歸納思維在數學各個階段、各個分支中都有着重要的作用，在中考題中還專門有探索規律的專題。他考察學生分析、比較、探索、歸納的能力。從變化中尋找不變，在不變中發現規律。這是同學們學習數學也是生活中必備的能力。
,更多精彩资讯请关注tft每日頭條，我们将持续为您更新最新资讯!
zpostcode 
Recruit 
weather 
mreligion 
Yellowpages 
sport 
constellation 
shopping 
name 
game 
directory 
literature 
Word 
tour 
furnish 
Lottery 
tftnews 
lyrics 
News 
digital 
car 
dir 
Edu 
Finance 
