大約在公元前450年，安那克薩哥拉斯（一位著名的古希臘哲學家）終于有了一些閑暇來思考，因為這位希臘數學家聲稱“太陽不是神，而是一塊像伯羅奔尼撒半島那麼大的發光岩石”而入獄。作為一位相信“理性統治世界”的哲學家，他曾在獄中提出了一個直到如今依然廣為人知的數學問題，“用圓規和直尺，你能否為一個給定的圓做出一個面積相等的正方形? （即化圓為方）”

令人驚訝的是，一直到今天數學家們仍在研究這個問題，上周由馬塞，諾伊爾和皮卡克在網上聯合發布的一篇論文就是在探讨這個古老問題，在論文中科學家們展示了如何通過将圓切割成可視化和可繪制的碎片來将圓形變換為同樣面積的正方形。

安那克薩哥拉斯提出的問題最早在1882年得到了證明，當時德國數學家費迪南·馮·林德曼證明了用經典工具（圓規和直尺）是不可能将圓形變更為同樣面積的正方形。他證明了π是一個超越數，超越數是一種無法被整除的無理數。你不可能畫出一個長度等于超越數的線段，也不可能畫出一個半徑等于超越數的圓。

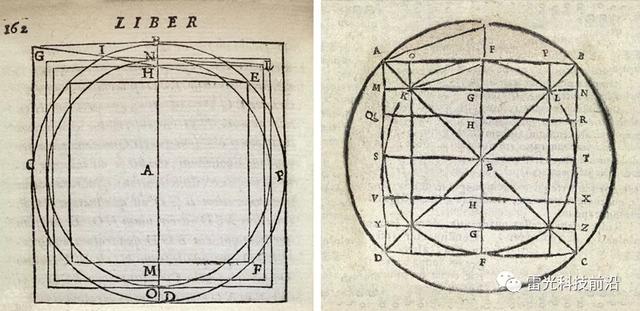
到這裡故事可能就結束了，但在1925年阿爾弗萊德•塔爾斯基通過改變前提使這個問題重新煥發了生機，不是使用圓規和直尺而是其它切割方法可以化圓為方嗎？他提出，是否可以通過将一個圓切成有限數量的小片，然後在一個平面内移動，再重新組裝成一個面積相等的正方形。換句話說，如果兩個物體可以被分成大小和形狀相同的碎片，那麼我們就可以完成這項任務了。

直到1990年拉茲科維奇回答了這個問題，并給出了一個明确的結論：一個圓可以被重新組合變成一個正方形。為了形象化拉茲科維奇的結論，我們可以想象在一頁紙上一個圓形和一個正方形并排在一起。他提出的觀點是，如果把一個圓最多分成1050塊碎片，這些碎片都是複雜且形狀奇特的，可以在不旋轉的情況下移動，直到它們完全填滿正方形。然而令人遺憾的是，這些碎片是如此地抽象以至于人們根本無法将這1050塊的碎片畫出來。

幾十年後，馬克斯和多倫多大學的斯賓塞·昂格一起，做出了重大的改進，提供了第一個完整的“化圓為方”的數學證明——通過嚴格的數學證明确定了切片的方式是普适的，沒有任何例外。“但是我們論文的缺點是”，馬克斯不得不承認，“即使從數學公式的角度上明确地定義并證明了我們的結論，然而遺憾的是我們很難将這些碎片可視化。” 在馬克斯的基礎上，我們本期的主角們，馬塞，諾伊爾和皮卡克等人更進一步。他們将圓一共切成了大約10200個碎片，更重要的是這些碎片形狀更簡單、可視化。

皮卡克甚至已經有了進一步的想法，減少碎片的總數或使它們形狀更均勻。他已經做了一些計算機實驗，這些實驗表明——盡管并沒有嚴格證明——可以用22個部件來完成化圓為方的結果，甚至他認為所需的碎片數量可以更小。

本文參考Quanta magazine文章，“An Ancient Geometry Problem Falls to New Mathematical Techniques”，如有興趣還可查閱原文。

如有侵犯版權還請告知，我們将在24小時内删除

更多精彩资讯请关注tft每日頭條，我们将持续为您更新最新资讯!