高中數學100個立體幾何方法-tft每日頭條

高中數學100個立體幾何方法

教育更新时间:2024-05-11 17:43:04

在高考試題中，立體幾何是必考試題，在解答題中立體幾何必有一題，且出題的模式相對比較穩定，題目的難度屬于中等或中偏下，但是從近幾年的試題分析來看，立體幾何題的得分情況不容樂觀，得分率比較低。參加高考閱卷的老師反映，很多學生一步也沒做。新教材的立體幾何的講解偏重于向量法，正确的建立直角坐标系，成為解題的關鍵，本文列舉了幾種常見的幾何模型，在這幾個幾何模型下，給出常見的建系方案！

高中數學100個立體幾何方法（高考數學立體幾何十類常見圖形）1

一、棱柱

①長方體，正方體等

天然擁有三條棱兩兩垂直的優勢，直接建系

高中數學100個立體幾何方法（高考數學立體幾何十類常見圖形）2

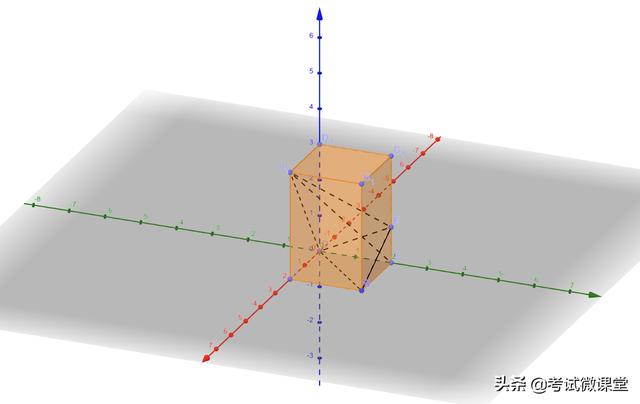
完成建系

高中數學100個立體幾何方法（高考數學立體幾何十類常見圖形）3

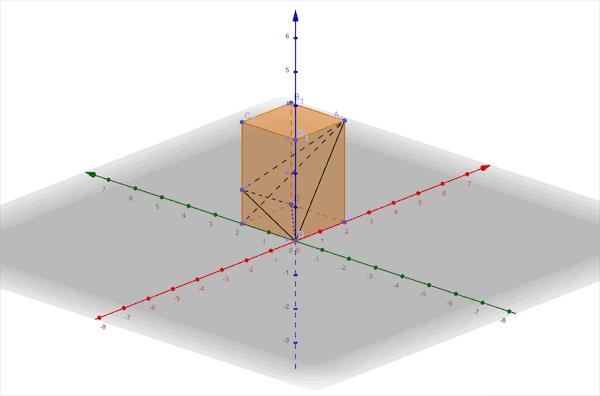
動态展示

②正三棱柱

依靠側棱垂直于底面，底面一個内角是60°，作出直角，建立坐标系

高中數學100個立體幾何方法（高考數學立體幾何十類常見圖形）4

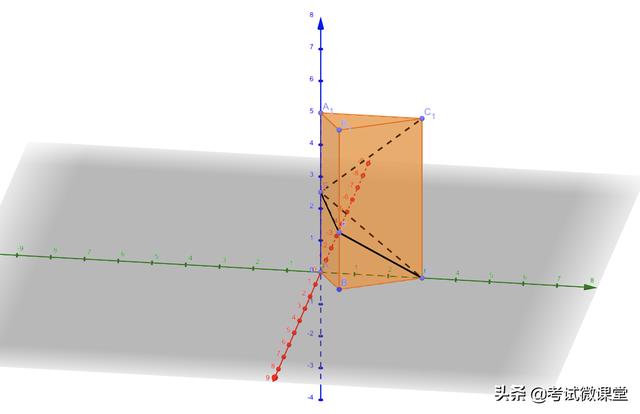
完成建系

高中數學100個立體幾何方法（高考數學立體幾何十類常見圖形）5

動态展示

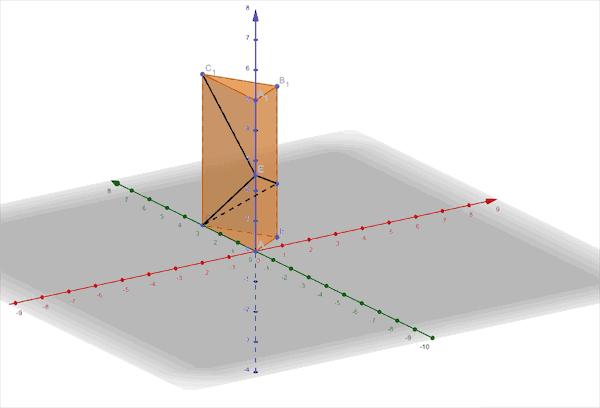
③橫置正三棱柱

高中數學100個立體幾何方法（高考數學立體幾何十類常見圖形）6

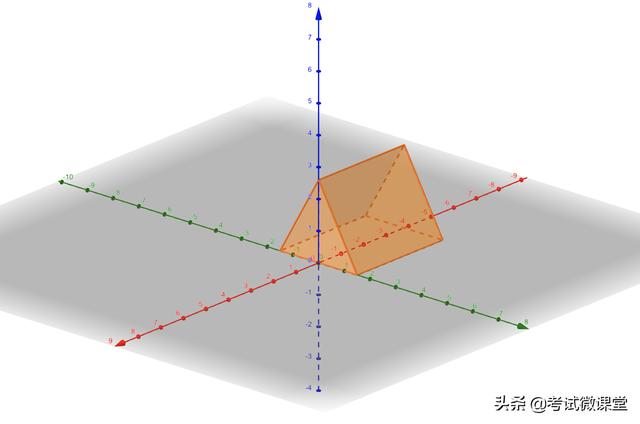
完成建系

高中數學100個立體幾何方法（高考數學立體幾何十類常見圖形）7

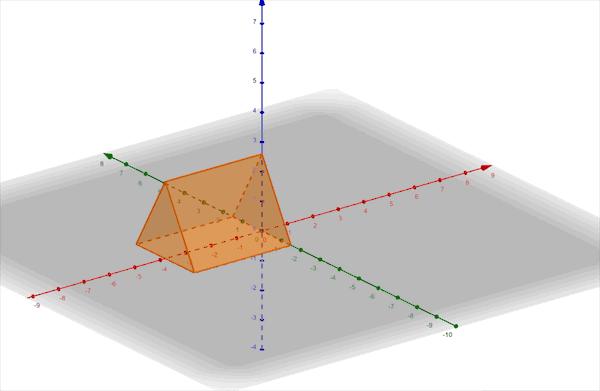
動态展示

二、棱錐

①側面與底面垂直的棱錐

依靠側面與底面垂直，在根據側面三角形的特殊性，先證明一條線垂直于底面，充當z軸

高中數學100個立體幾何方法（高考數學立體幾何十類常見圖形）8

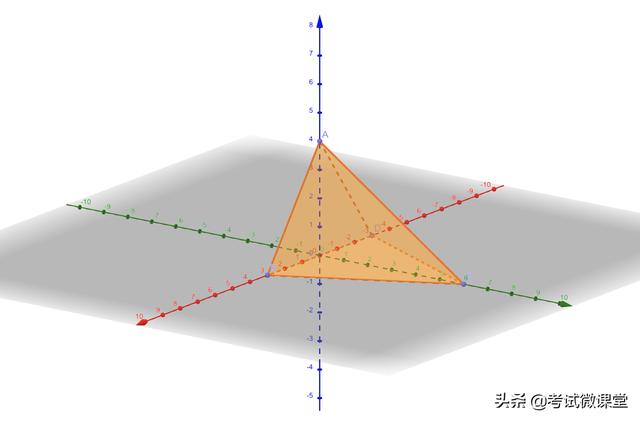
一步建系

高中數學100個立體幾何方法（高考數學立體幾何十類常見圖形）9

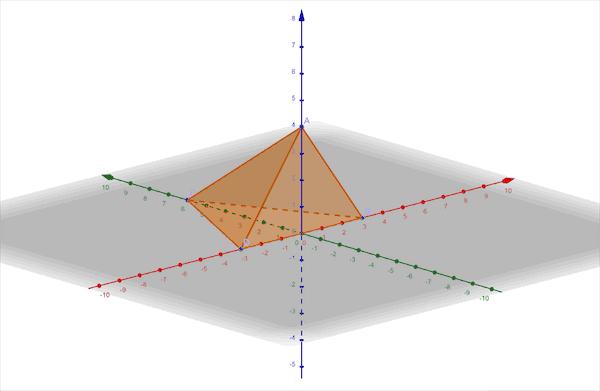
動态展示

②正三棱錐

高中數學100個立體幾何方法（高考數學立體幾何十類常見圖形）10

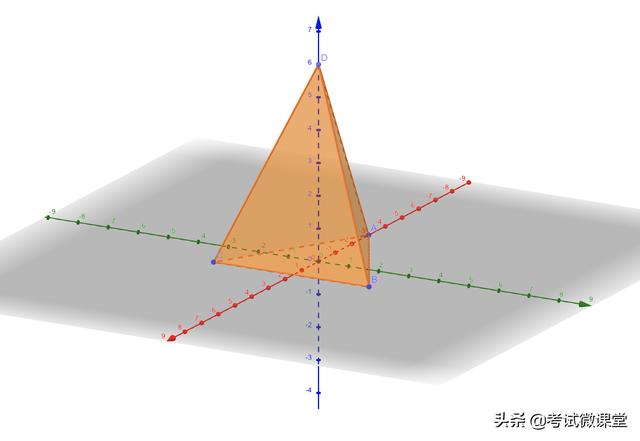
一步建系

高中數學100個立體幾何方法（高考數學立體幾何十類常見圖形）11

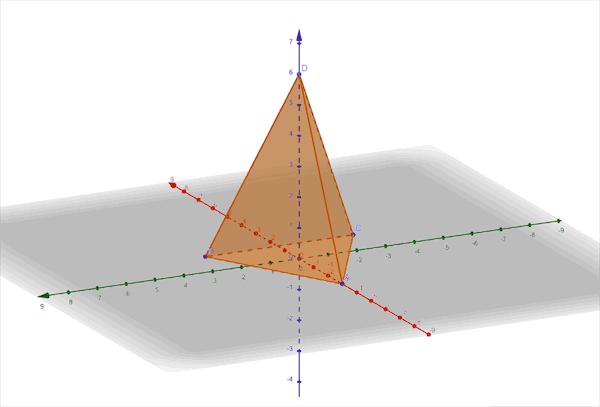
動态展示

③底面矩形四棱錐（頂點射影在中心）

依靠矩形相鄰兩邊互相垂直

高中數學100個立體幾何方法（高考數學立體幾何十類常見圖形）12

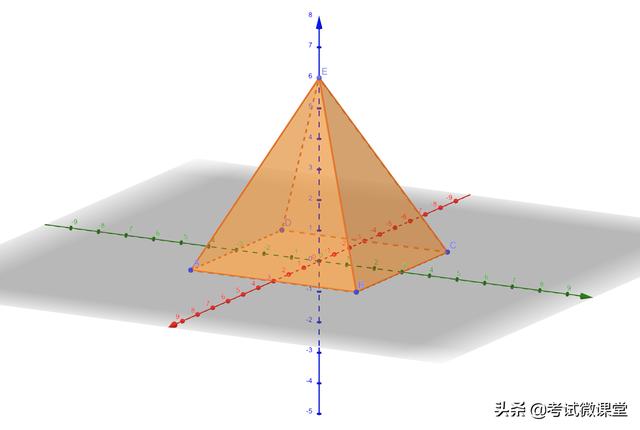
一步建系

高中數學100個立體幾何方法（高考數學立體幾何十類常見圖形）13

動态展示

④底面菱形四棱錐（頂點射影在中心）

依靠菱形對角線互相垂直

高中數學100個立體幾何方法（高考數學立體幾何十類常見圖形）14

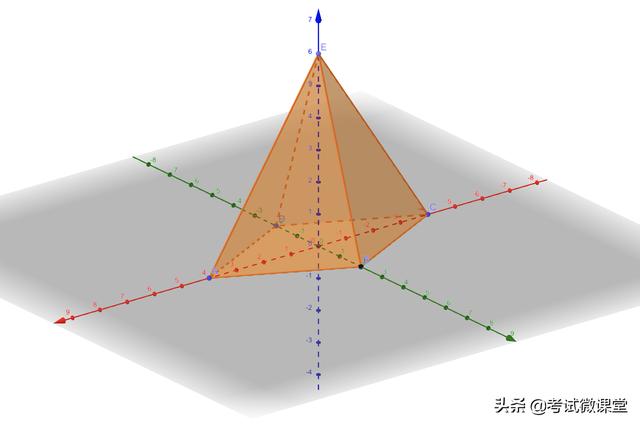
一步建系

高中數學100個立體幾何方法（高考數學立體幾何十類常見圖形）15

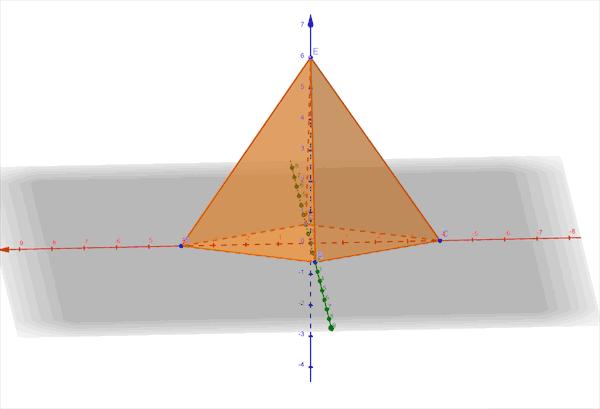
動态展示

⑤正四棱錐

以上兩個做法均可

三、棱台

以三棱台為例

高中數學100個立體幾何方法（高考數學立體幾何十類常見圖形）16

一步建系

高中數學100個立體幾何方法（高考數學立體幾何十類常見圖形）17

動态展示

動态圖像由Geogebra制作，感興趣的朋友歡迎評論區留言

更多精彩资讯请关注tft每日頭條，我们将持续为您更新最新资讯!

查看全部

网友关注

教育閱讀簽字家長怎麼簽
閱讀簽字家長這樣簽既真誠又符合要求：1、首先表達家長對孩子讀書态度的肯定。如：孩子讀完《XX》這本書... 2023-07-07
教育黃梅時節家家雨的意思
1、黃梅時節家家雨的意思：梅子黃時，家家都被籠罩在雨中。2、《約客》作者：趙師秀黃梅時節家家雨，青草... 2023-07-07
教育一萬年太久隻争朝夕的意思
1、“一萬年太久，隻争朝夕”的意思是在一萬年後才取得勝利，這實在是太久了，我們要争取利用更多的時間。... 2023-07-07
教育日環食發生在什麼時候
1、在陽光照射下，月亮和地球在du背向太陽的方向拖着一條影子。月亮掃過地zhi面，産生了日食。日食必... 2023-07-07
教育難過的詞語
1、哀涼，哀鳴，哀歎，哀凄，愁悶，愁苦，愁思，愁緒，憂愁，憂郁2、悲歎，哀傷，悲觀，哀痛，哀愁，哀憐... 2023-07-07
教育 985211雙一流大學名單
1、雙一流大學名單包括兩部分。2、世界一流大學，42所，是在原有39所985院校基礎上增加了鄭州大學... 2023-07-07
教育曾子殺豬文言文
1、原文曾子之妻之市，其子随之而泣。其母曰：“女還，顧反為汝殺彘（zhì）。”妻适市來，曾子欲捕彘殺... 2023-07-07
教育醉翁亭記原文
1、環滁皆山也。其西南諸峰，林壑尤美，望之蔚然而深秀者，琅琊也。山行六七裡，漸聞水聲潺潺，而瀉出于兩... 2023-07-07
教育幼兒園老師分享正能量的一段話
1、幼兒園畢業啦，讓我的祝福像那美麗的娃娃陪伴在你的身邊，伴你健康的成長！2、飛吧，飛吧，在生活的田... 2023-07-07
教育 2020年報考哪些專業就業前景較好
1、一般來說文科裡面比較好的專業也像經濟管理類專業，比如說金融學專業，經濟學專業，會計學專業，管理學... 2023-07-07
教育财務報表如何做
1、準備：每個月将公司的一切财務狀況，包括收入、支出、納稅等等用表格記錄下來，并在月末和年末将每個項... 2023-07-07
教育年利率公式
1、年利率總額是指本息合計金額，按照單利和複利兩種方式計算。單利計息：年利率＝1＋月份*每月利率複利... 2023-07-07
教育舉世矚目是什麼意思
1、舉世矚目，漢語成語，拼音是jǔshìzhǔmù，意思是指全世界的人都注視着，形容影響很大。2、近... 2023-07-07
教育 rst是什麼意思
1、RST代表複位電路的意思。2、RST是RESET的簡寫,RESET信号一般用于有CPU的電路中,... 2023-07-07
教育千山萬水總是情的意思
1、意思是即使遠隔萬水千山也難舍那份情牽挂。表達了對愛情的堅貞不渝。千山萬水總是情出自于《秋思》2、... 2023-07-07
教育但少閑人如吾兩人者耳翻譯
1、但少閑人如吾兩人者耳翻譯：隻是缺我們兩個清閑的人罷了閑人：無事可做閑适自得。2、原文：元豐六年十... 2023-07-07
教育八面玲珑打一生肖
1、老鼠。玲珑：精巧細緻，指人靈活、敏捷。原指窗戶寬敞明亮，後來用來形容人處（鼠）事圓滑，不得罪人。... 2023-07-07
教育 2020年開學第一課觀後感
每一年的開學第一課我都會有很大的收獲，因為它陪伴了我很多年，從小學一年級到現在，每一次都學到不少新的... 2023-07-07
教育九十八和一是什麼意思
1、九十八和一意思是雜（上面是個九,下面是個十和八）鐘（和加一豎）。還有一句完整的,春蟲蟲九十八和一... 2023-07-07
教育主持詞範文
1、各位親愛的嘉賓，朋友們：大家晚上好！首先非常感謝大家在百忙之中抽出寶貴的時間來參加泛華金融集團湖... 2023-07-07
教育春華秋實的近義詞
1、春華秋實近義詞：開花結果。2、意思是春天開花，秋天結果。比喻人的文采和德行。現也比喻學習有成果。... 2023-07-07
教育關于教師節的作文
1、教師節：九月十日，是個人人皆知的日子——教師節。在這即将來臨的節日裡，我衷心地向老師說一聲：“老... 2023-07-07
教育大學教師算什麼編制
1、在編老師為事業單位工作人員。非在編教師即為臨聘人員或者稱作合同工。2、教師作為事業單位工作人員，... 2023-07-07
教育關于感恩節的英語資料
1、感恩節由來Thanksgivingdayistheunitedstatesandcanada,t... 2023-07-07
教育湯姆索亞曆險記概括50字
1、《湯姆索亞曆險記》這本書記述了主人公湯姆·索亞因反對死闆嚴格的家庭生活，厭煩學校裡枯燥乏味的功課... 2023-07-07
教育四大文明古國是什麼
1、四大文明古國，華夏關于世界四大古代文明的統稱。分别是古巴比倫（位于西亞，今地域屬伊拉克）、古埃及... 2023-07-07
教育中秋節作文怎麼寫
1、既然是佳節，就要盡情地玩。玩是積累生活素材。你不玩，寫作就缺少素材，即使你是”巧婦“，也難為”無... 2023-07-07
教育錢學森觀後感
1、看完電影《錢學森》，深深地被偉大的科學家錢學森堅貞的民族氣節和崇高的愛國精神所感動。同時，也深刻... 2023-07-07
教育節約用電标語
1、冷氣空調要省電，溫度控制要做好。2、照明品質要提高，省電燈具不可少。3、節約用電，人走燈滅。4、... 2023-07-07
教育大展鴻圖與大展宏圖有什麼區别
1、“大展宏圖”的“宏”是指宏偉壯觀，主要形容建築，建設，或者事業方面。“大展鴻圖”的“鴻”是天鵝的... 2023-07-07

tft每日頭條

> 教育

> 高中數學100個立體幾何方法

高中數學100個立體幾何方法

相关教育资讯推荐

热门教育资讯推荐

网友关注