用代碼畫畫，必需要懂很多數學知識？如果數學基礎沒那麼好，是否就無法肆意表達，領略其中的樂趣？

其實不然。很多時候，隻要用簡單的數學知識，也能做出複雜精妙的作品。

希望通過下文，可以讓你破除對數學的恐懼，從基礎的概念入手，與三角函數“共舞”。

什麼是三角函數？

如果要問哪個數學函數在圖形創作上使用頻率最高，那三角函數估計能排在前幾位。

三角函數，用簡單的話來講，是用來描述直角三角形邊長和角度關系的函數。常用的三角函數有正弦函數（ sin ），餘弦函數（ cos ），正切函數（ tan ）。

用一張圖來舉例。假如有一個直角三角形 ABC,其中 a,b 是直角邊,c 是斜邊。

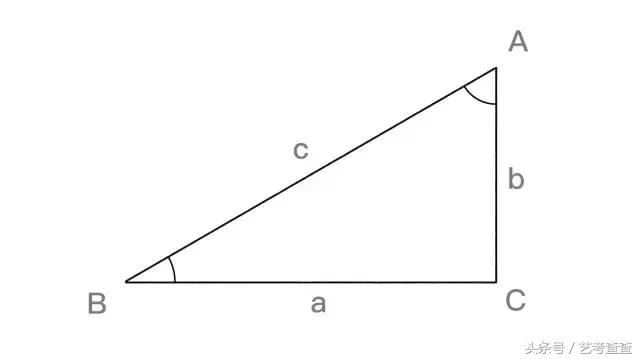
關于三角函數我們可以記住這樣一個性質：直角三角形中，邊與角的這種比例關系是固定的，所以無論是多大或多小的三角形，隻要兩個三角形比例相似，相對應兩個角的 sin 值，總是恒定的，因為邊長的比例固定。反過來，如果我們已知某三角形某個角的 sin，cos 或 tan 值，結合一定條件，也能反過來推算出角度值。

為了更好地理解，這裡再拿一個特殊的直角三角形來舉例。假如一個直角三角形它的各個角分别為 30 度，60 度，90 度。那它的對邊之比，就分别為 1：√3：2。

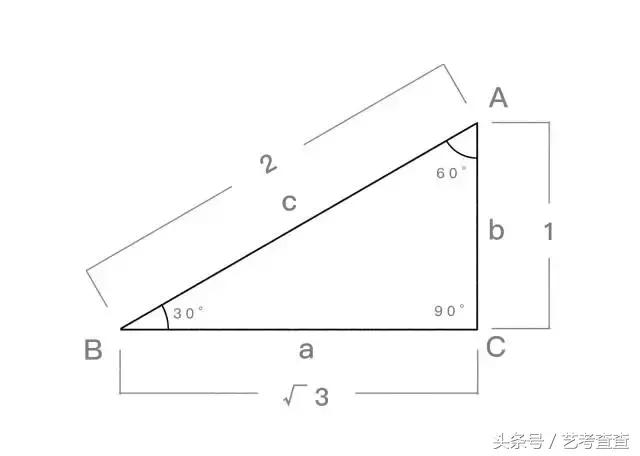
現在，我們隻要将各邊對應的比例關系代入，就能手動計算出正弦函數和餘弦函數的數值。比如 sin 30 度就為 1/2 ，即 0.5。cos 30 度就為 √3/2,約等于 0.866。

這就是三角函數的數學定義。看到這裡，相信你已經對它有了基本的了解，接下來我們可以學習在程序上的使用方法。

在 Processing 中使用三角函數

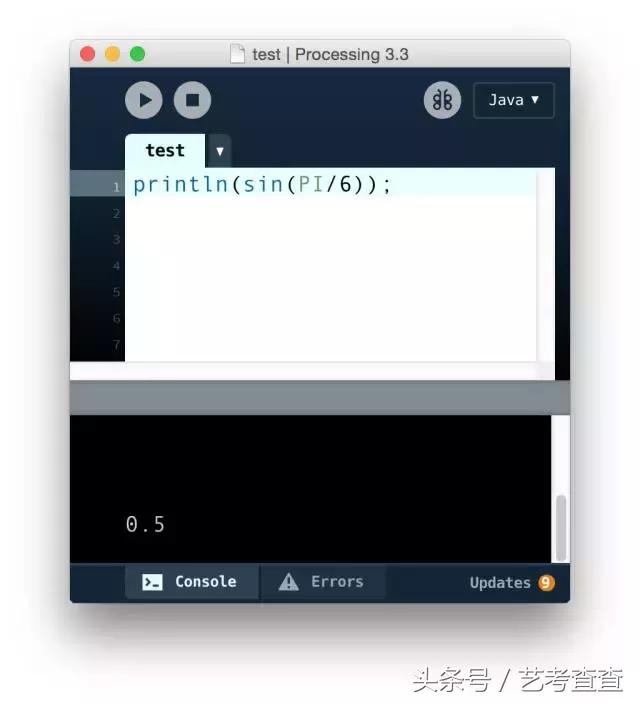
假如我們現在需要用程序來直接獲取 sin 30 度的值，可以在 Processing 中這麼寫。

println(sin(PI/6));

輸出結果為 0.5

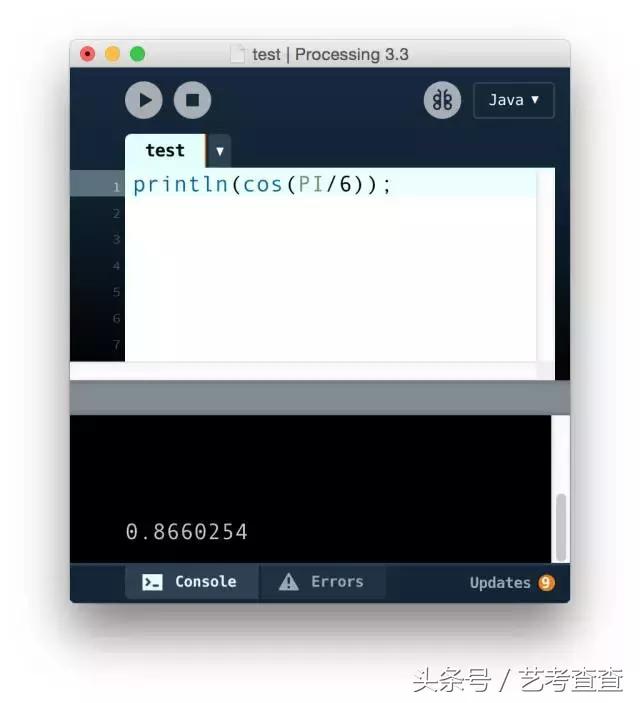
cos 30 度，則是這麼寫

println(cos(PI/6));

結果約等于 0.866

但為何這裡寫的是 PI/6,而不是 30？這是因為 Processing 中規定，sin 函數中傳入的參數采取的是弧度制。

所謂的弧度制，就是用單位圓的弧度長來表示角度。

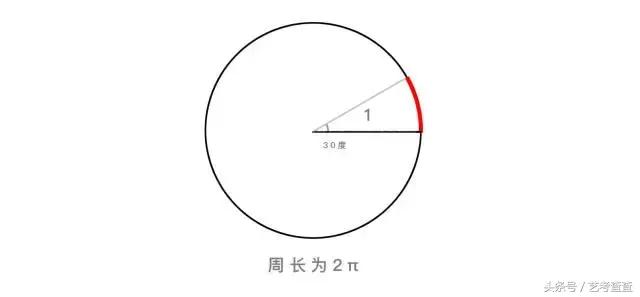
假設單位圓的半徑為 1。根據周長公式 l = 2 π r, 那圓的周長就是 2 π。而 2 π 的弧長（周長），就對應 360 度。同理,一個角的角度如果是 30 度。那它對應的弧長（圖中紅線部分），就為整個圓弧長十二分之一，即 2 * π / 12，為 PI / 6。

所以程序中寫 sin(PI/6) ,意思就是求 30 度的 sin 值是多少。

當然，如果你更習慣用角度制來表示。程序中還可以這麼寫，隻要使用函數 radians,它就能自動将角度值換算成弧度值，相當方便。

println(sin(radians(30)));

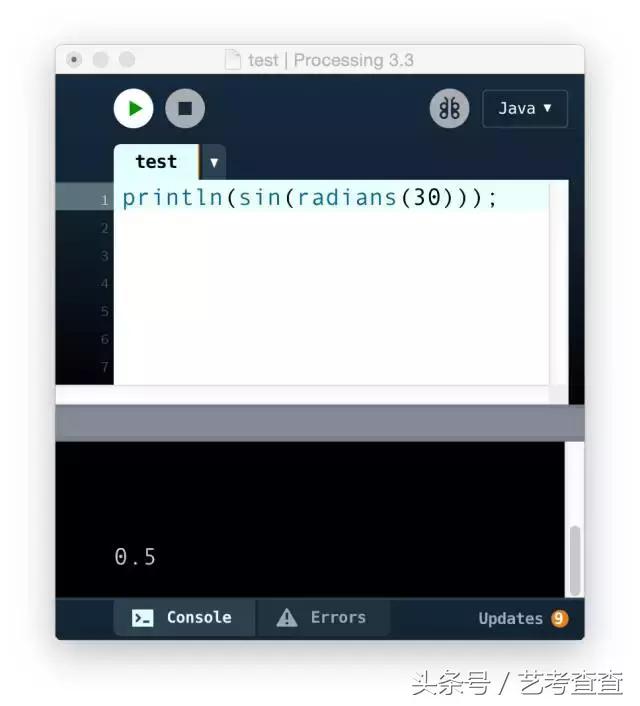
輸出結果與原來一樣,都為 0.5。

通過圖像中認識三角函數

前面鋪墊完基礎知識，下面就進入正題，開始在程序中作畫。首先，我們需要把三角函數的函數曲線畫出來

繪制函數曲線

例子01：

PVector posA, posB; void setup() { size(700, 400); background(255); posA = new PVector(0, 0); posB = new PVector(0, 0); } void draw() { float speed = 0.02; posA.x ; posA.y = height/3 sin(posA.x * speed) * 40; posB.x ; posB.y = height/3 * 2 cos(posA.x * speed) * 40; strokeWeight(5); point(posA.x, posA.y); point(posB.x, posB.y); }

代碼淺析：

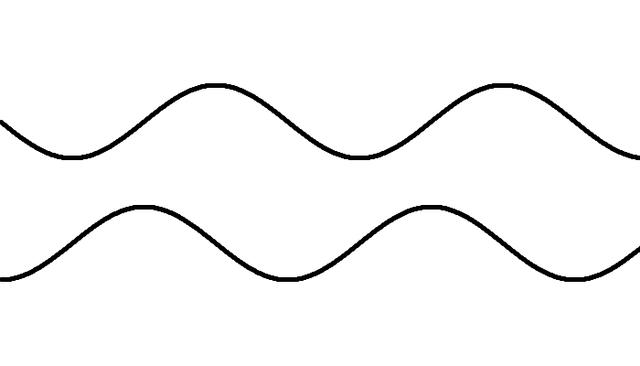
• 例子中為了方便對比，同時繪制了 sin 和 cos 函數的圖像。其中 PVector 代表向量，常用用于表示點坐标

• A ,B 兩點的橫坐标都不斷遞增，這個遞增值作為自變量，傳入到 sin 和 cos 函數中便獲得輸出值，接着把輸出值的變化，賦值到 A,B 兩點的縱坐标上

• background 寫在 setup 函數中，會使得 A,B 兩點移動的軌迹保留在畫布上

• 從上圖可以發現，sin 和 cos 的圖形呈現周期變化。圖形的大小比例完全相同的，隻是在 x 軸方向的位置有所不同。

接下來，我們試着在上例的基礎上，把 speed 的值改成 0.2

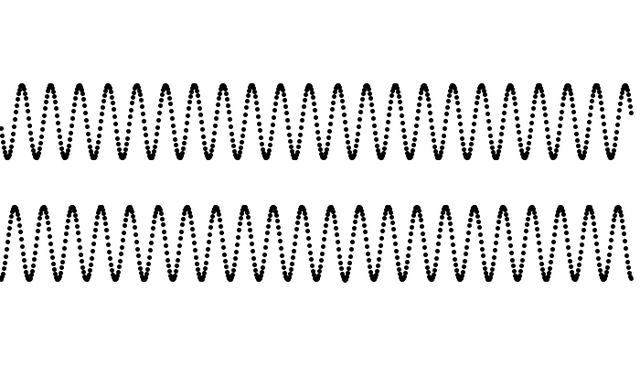
又或是改得非常小，寫成 0.005；

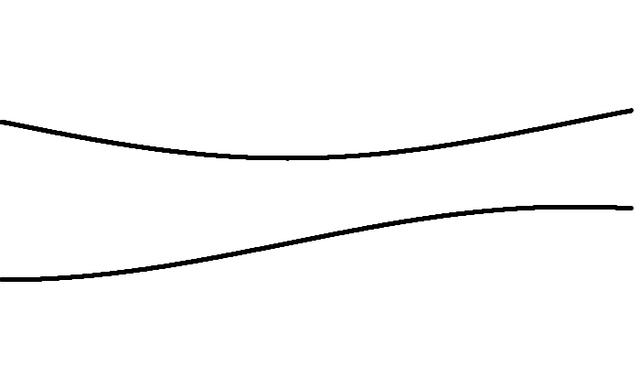
對比原圖，會發現圖形被拉伸或是壓縮。這是由于輸入值的變化速度發生改變了。輸入值變化越慢，輸出值也會越慢，因而起伏越小。

如果在繪制的時候，我們還想嚴格地控制“波峰”“波谷”的數量。那就需要注意輸入值的變化範圍。

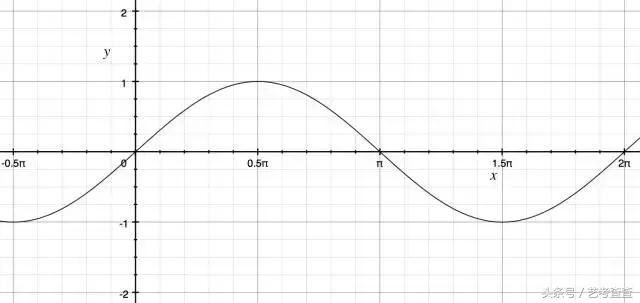
由于 sin 函數和 cos 函數，他們的周期都為 2 π。所以當輸入值的範圍恰好是 2 π 的整數倍時，就可以在屏幕上繪制出與倍數相同的“波峰”“波谷”，并且是可以首尾銜接的。

試着将 speed 寫成

float speed = 2 * PI * 0.01;

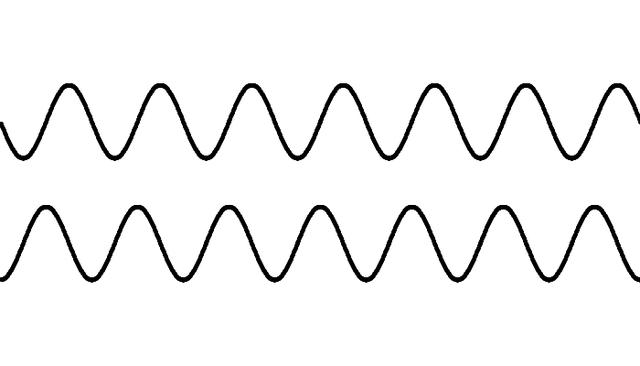
因為屏幕寬為 700，所以恰好就能繪制出 7 段重複的波形，可以代入到例子中仔細思考其中的含義。

三角函數的簡單應用

在程序中使用三角函數，基本就是靠這個輸出值來做文章。因為 sin 和 cos 函數是可以互相轉換的，所以在具體應用時，使用 sin 還是 cos 并沒有太大差别。

現在，試着把 sin 值的變化，映射到圓的半徑，就能産生這樣的效果

例子02：

void setup() { size(700, 400); } void draw(){ background(255); float l = sin(frameCount/100.0) * 200; fill(0); ellipse(width/2,height/2,l,l); }

映射到角度

例子03：

void setup() { size(700, 400); } void draw(){ background(255); float angle = sin(frameCount/100.0) * PI/2; translate(width/2,height/2); rotate(angle); rectMode(CENTER); fill(0); rect(0,0,200,200); }

映射到圓的位移，利用輸入值的差異産生錯落效果

例子04：

void setup() { size(700, 400); } void draw() { background(255); fill(0); for (int i = 0; i <= 7; i ) { float h = sin(i/2.0 frameCount/10.0) * 100; ellipse(i * 100, 200 h, 80, 80); } }

從上面三個小實例可以看出，若想精确地控制圖形元素，就要熟悉它的周期性，控制它的輸入輸出範圍。位移的多少，角度的變化快慢，都與之息息相關。

使用三角函數實現圓周運動

三角函數的一個重用應用，就是使用它畫圓

例05:

PVector pos; void setup(){ pos = new PVector(); } void draw(){ background(255); float r = 180; pos.x = r * cos(frameCount/100.0); pos.y = r * sin(frameCount/100.0); translate(width/2,height/2); fill(0); ellipse(pos.x,pos.y,40,40); }

具體原理可以查看下圖，它可以根據三角函數的定義推導得出。想象在圓周上有一個黑色圓點在運動，它構成的直角三角形的兩個直角邊，就對應它的坐标值。

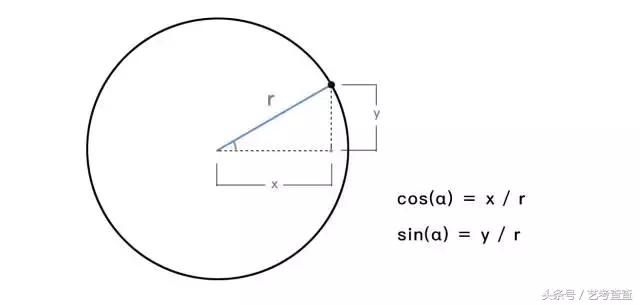
而從中圍成的三角形，由于

cos(α) ＝ x / r sin(α) ＝ y / r

很容易能推出

x = r * cos(α)y = r * sin(α)

所以我們隻要在 α 處，傳入一個不斷自增的參數。x，y 的坐标就會輸出圓周運動。

網上有其他朋友制作了這樣一張動圖，非常形象直觀地揭示了底層原理

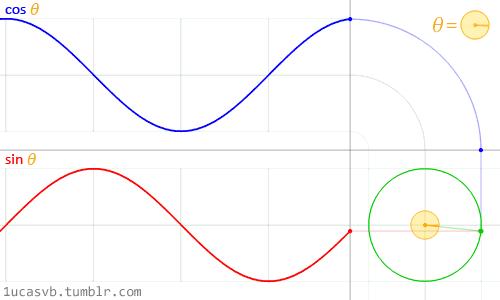
巧妙！

綜合應用

前面介紹的圓周運動，經過特殊組合，可以“編織”出一些非常有意思的圖案

例06:

PVector posA,posB; void setup(){ size(700,700); background(0); posA = new PVector(); posB = new PVector(); } void draw(){ float r1 = 300; float speed1 = frameCount/100.0 * 4; posA.x = r1 * cos(speed1); posA.y = r1 * sin(speed1); float r2 = 150; float speed2 = frameCount/100.0; posB.x = r2 * cos(speed2); posB.y = r2 * sin(speed2); translate(width/2,height/2); stroke(255,100); line(posA.x,posA.y,posB.x,posB.y); }

代碼淺析：

• 這裡設定了兩個做圓周運動的點，并對它們進行連線。由于兩點的運動半徑以及運動速度都不一緻，所以就使得直線在交織時，産生深淺不一的效果

試着改變傳入的速度，半徑

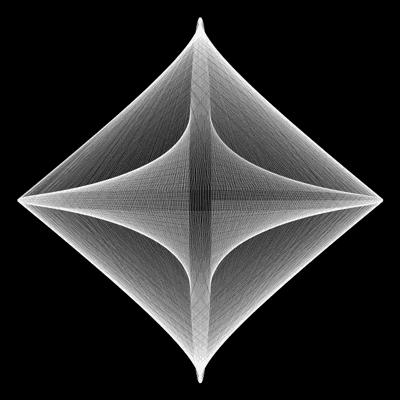
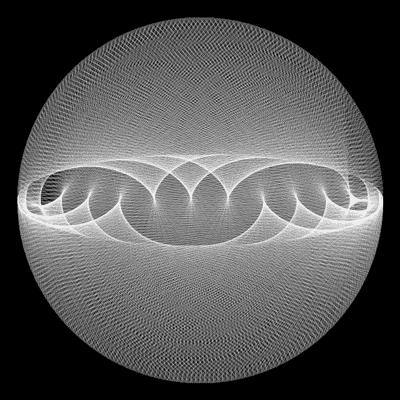
也可以開啟疊加模式，實時改變線條的顔色

例07:

PVector posA,posB; void setup(){ size(700,400); background(0); posA = new PVector(); posB = new PVector(); } void draw(){ float r1 = 300; float speed1 = frameCount/300.0 * 4; posA.x = r1 * cos(speed1); posA.y = r1 * sin(speed1); float r2 = 150; float speed2 = frameCount/300.0; posB.x = r2 * cos(speed2); posB.y = r2 * sin(speed2); translate(width/2,height/2); colorMode(HSB); blendMode(ADD); stroke(frameCount/10.0 % 255,255,255,30); line(posA.x,posA.y,posB.x,posB.y); }

下面的圖片都是在同一個結構中，修改不同參數産生的。隻是畫布設置得更大，同時讓線條的運動變得更平緩，這樣就能産生豐富細膩的層次變化

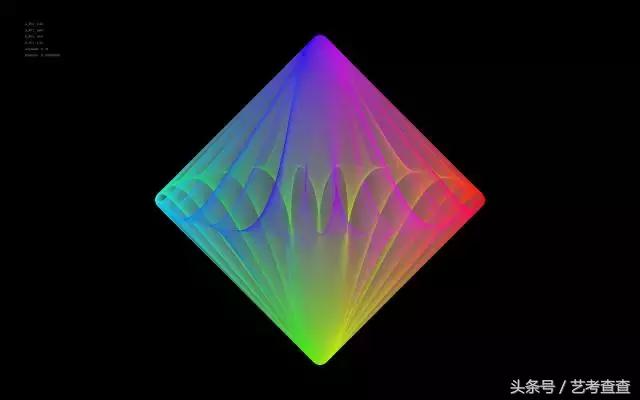
利用 sin 函數實現動态畫筆

接下來再分享兩個有關畫筆的實例，這節的介紹就快到尾聲

先看基礎版

例08:

ArrayList<PVector> brushLines = new ArrayList<PVector>(); void setup() { size(700,700); } void draw() { background(0); for (int i = 0; i < brushLines.size(); i ) { PVector tempPos = brushLines.get(i); float l = sin(frameCount/20.0 i/4.0) * 50; ellipse(tempPos.x,tempPos.y,l,l); } } void mouseDragged() { brushLines.add(new PVector(mouseX, mouseY)); }

拖動鼠标，就會記錄繪制軌迹。sin 函數此時會控制圓點的半徑。

下面再看加強版

例09:

ArrayList<PVector> brushLines = new ArrayList<PVector>(); PImage myPic; void setup() { size(1200, 700); myPic = loadImage("pic.jpg"); myPic.resize(width, height); } void draw() { background(0); noStroke(); tint(125); image(myPic, 0, 0); for (int i = 0; i < brushLines.size(); i ) { PVector tempPos = brushLines.get(i); float r = 10 * sin(i/3.0 millis()/200.0); fill(myPic.get(int(tempPos.x), int(tempPos.y))); ellipse(tempPos.x, tempPos.y, r, r); } } void mouseDragged() { brushLines.add(new PVector(mouseX, mouseY)); } void keyPressed(){ if(key == 'c'){ brushLines.clear(); } }

拖動鼠标繪制圖案，按 c 鍵清空畫布

在運行實例前，需要先尋找一張圖片素材放到所在文件夾中，來作為程序的背景圖片。繪制的筆觸會吸取背後的圖片顔色，與經過變暗處理的背景相組合，就會産生類似于發光的效果。推薦使用梵高的作品做測試，絢麗的色彩和奔放的筆觸，會更相得益彰。

如果做出滿意作品，可以試着導出 Gif （Processing3.0 Gif動圖導出技巧）

三角函數其他應用

三角函數還有其他用法嗎？非常多。最後再截選一些之前的習作，它們都有用到三角函數。

（控制關節的旋轉角度，模拟翅膀擺動效果）

（使用三角函數确定關節坐标）

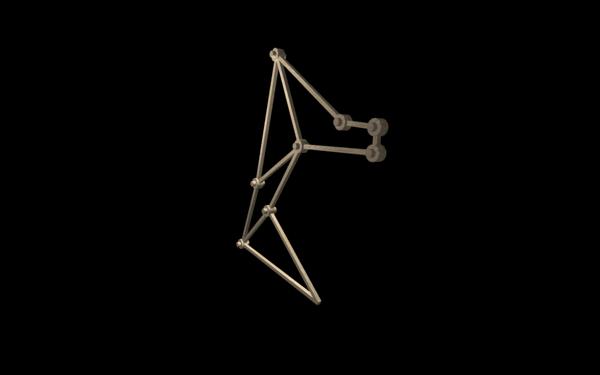
（已知方向和步長，計算下個生長的坐标點）

藝考查查全國首發2018年各地統考聯考報名時間表，2018年藝考重要招生錄取信息，2018藝考簡章彙總等。每天，我們将會為全國藝術生推送藝考信息，讓你在第一時間詳細而全面的掌握藝考相關信息，不會有後顧之憂。有我們的一路陪伴，藝考之路，不會孤單不會害怕。總有一天，你揮灑汗水，會凝結成晶瑩剔透珍珠閃閃發光。

更多精彩资讯请关注tft每日頭條，我们将持续为您更新最新资讯!