在這篇文章中，我們将用一種非常優雅和簡單的方式證明數論中的一些驚人的定理，使用一種非常強大的理論，即狄利克雷卷積。我希望通過向你們展示這個理論與解析數論和黎曼ζ函數之間的聯系，讓它成為初等數論和解析數論之間的橋梁。
算術函數（數論函數）
算術函數，也就是，所有以值1、2、3、…為參數的函數。這樣的函數f被定義為每一個自然數n的複值f(n)，盡管f(n)的值通常是自然數。從現在開始，字母n, m和k将表示自然數，除非另有說明。
積性函數
算術函數的定義很廣。有一些簡單的性質是非常重要的。我們定義了n和m之間的最大公約數，即gcd(n, m)除以能将兩者同時整除的最大自然數，例如gcd(12,18) = 6。
一種算術函數f被稱為積性函數，如果對于任意一對n和m, gcd(n, m) = 1，有f(nm) = f(n)f(m)，也就是說，當n和m是互素時，這個性質成立。如果這個對任意n和m都成立，那麼我們稱f為完全積性。
這些函數在整個數論中起着重要的作用。一個重要的函數族是“除數函數和”的集合，我們稍後會回到這個問題。
因子求和
這個理論都是關于算術函數的值的和，用n的除數來表示。
讓我們從一些符号開始。d|n時意思是d除以n。設g為算術函數。然後可以用以下方法定義一個算術函數f：
例如，f(8) = g(1) g(2) g(4) g(8)，因為8的因數是1、2、4和8。
一個驚人的性質是成立的，即如果上面的函數g是積性的，那麼f也是積性的。
為了理解這一點，假設g是一個乘法函數，且n和m是互質的，即gcd(n, m) = 1，那麼：
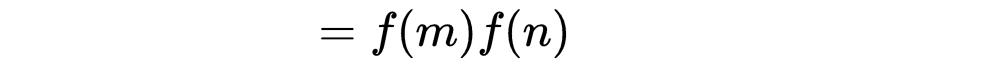
說明f是積性的。注意，第一個等式是因為上面的定義；在第二個等式中，我們使用的乘積nm的除數必須分别是n和m的除數的乘積，這是因為m和n是互素的；在第三個等式中，g是積性的；在第四個等式中，我們使用分配律來确保所有的和組合都被考慮在内。
從剛才證明的引理中，我們立即知道，許多已知的和常用的算術函數實際上是積性的，例如除數函數。
函數f和g之間的這種關系起着特殊的作用，非常重要。從這個定義中産生了許多自然的問題。
有什麼已知的函數也是這樣的嗎（比如上面的f和g）？
有了上面的這些，我們能把g寫成f的形式嗎？也就是說，我們能把上面的公式颠倒一下嗎？如何做到？
接下來，我将回答這些問題，并提供一個可以用于研究的工具。
特殊的算術函數
縱觀算術函數理論，有些函數比其他函數更重要。在微積分中，指數函數和三角函數是非常重要的（當然是相互聯系的）；在代數中，多項式是非常重要的（它們幾乎在任何理論中都存在）；在解析數論中，有γ函數，黎曼ζ函數，模形式等等。
因此，對算術函數理論中具體函數的研究具有十分重要的意義。
恒等函數和單位函數
我們定義了以下重要的算術函數：
用以下方法定義恒等函數I：
這将在後面扮演一個特殊的角色。
我們定義單位函數u：
和函數N：
歐拉函數ϕ
這個函數已經被研究了好幾百年，而且确實是其中的一個亮點。該函數由ϕ表示，表示小于等于n的正整數中與n互質的數的數目.。例如：
ϕ(1)= 1
ϕ(6)= 2
ϕ(7)= 6
ϕ(10)= 4
通常，如果p是素數，那麼ϕ(p) = p - 1。一般來說，我們可以這樣定義它：
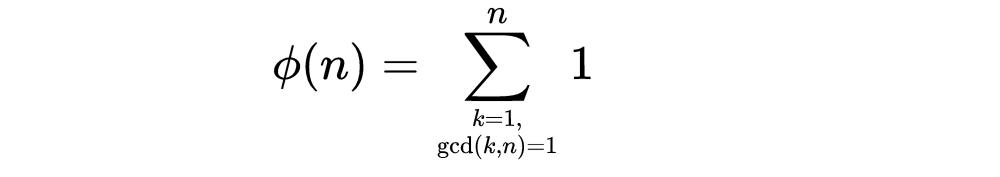
這個函數在數論和群論中有幾個重要的性質，但我們現在不進一步研究它。
我們現在需要知道的唯一一件事是ϕ是積性的。
莫比烏斯函數μ
默比烏斯函數在解析數論中也是一個非常重要的函數，并且是算術函數理論的核心。
我們用以下方式來定義它：
μ(1)= 1。假設一個自然數n，如果n能被m^2整除，那麼μ(n) = 0。注意，這意味着如果n能被一個大于1的素數的幂整除，那麼μ(n) = 0，因為那個素數的平方也能整除它。
如果沒有平方數能整除n，那麼有兩種可能：如果能整除n的素數是奇數，那麼μ(n) = -1；如果能整除n的素數是偶數，那麼μ(n) = 1。
我們可以證明莫比烏斯函數的等價定義：
μ是相乘的，μ的前幾個值是：
除數函數
古希臘人研究了數的可分性，知道了完美數、親和數等等。除數函數也與解析數論中的狄利克雷級數理論密切相關。我們稍後會講到。
最常被研究的兩個除數函數是：
上述函數的定義與你所想的完全一緻。d計算因子的個數，所以d(3) = 2， d(6) = 4。σ是因子和函數，所以σ(3) = 4， σ(6) = 12。
一般來說，我們可以通過以下方法定義第k個除數函數：
上面兩個函數隻是特殊情況。特别地，當k=0時，我們得到d；當k=1時，得到σ。
它們都是積性的，根據上面的引理，我們可以用求和的乘法性來得出這個結論。實際上，k可以是任意複數，但這裡我們不考慮這個。
狄利克雷分布
有了這些先決條件，我們現在就可以開始進入算術函數的世界了。如果f和g是算術函數，那麼它們的狄利克雷卷積就是f * g定義的算術函數：
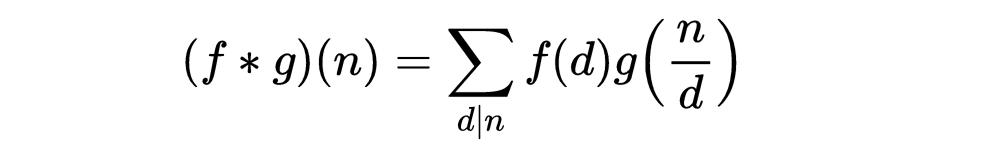
注意，這個運算實際上是對稱的，即f*g = g*f，由于乘法運算是對稱的，因此f(m)g(k)和f(k)g(m)都将出現在和中。你也可以看到，如果d是n的除數，那麼n/d也是。
我們也有：
其中I是上面定義的恒等函數。事實上，這就是它被稱為“同一性”的原因。
這很有趣，因為現在我們可以問下面的問題：
對于算術函數f是否存在一個函數g使f*g = I
結果是，如果f(1)≠0，那麼f就有一個逆（關于狄利克雷卷積）。這使得所有可逆算術函數的集合成為一個交換群，這個交換群是整個理論的中心。
注意，上面μ的定義可以寫成μ * u = I，說明μ和u是彼此的逆。這些函數具有逆函數的事實與數論中的一個主要結果密切相關：
定理（莫比烏斯反演公式）
設f和g是算術函數。如果：
對于所有的n，那麼：
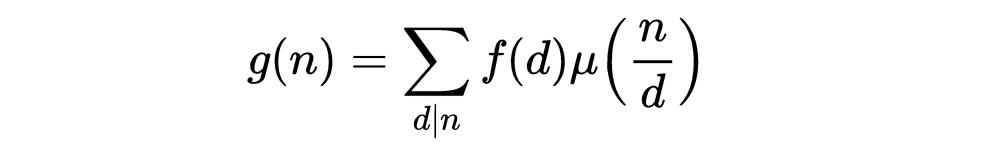
對于所有n。
為了證明這一點。首先，我們用狄利克雷卷積來重述它。這個定理說：
如果f = g * u，那麼g = f * μ。
證明：
如果f = g * u那麼 f * μ = (g * u) * μ = g * (u * μ) = g * I = g。
證畢。
這是一個簡單的證明，優雅而美麗。這個證明通常需要更多的論證和計算。我們還得到了其他一些漂亮的結果：
顯示著名的算術函數之間的關系。例如，到最後一個結果，我們有：
N(6) = 6 = σ(1)μ(1) σ(2)μ(2) σ(3)μ(3) σ(6)μ(6) = 1 - 3 - 4 12。
狄利克雷級數
我們還沒有真正涉及到狄利克雷卷積的起源以及它們為什麼如此重要。其中一個原因是狄利克雷級數。狄利克雷級數是這種形式的級數：
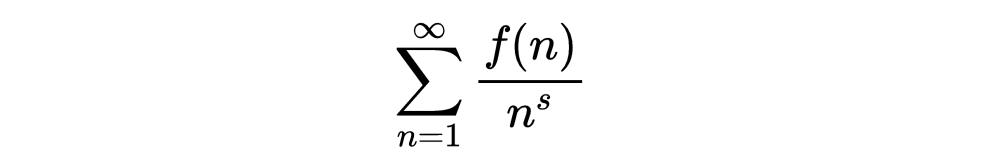
其中f是一個算術函數s是一個複變量。因此，這實際上是一個複變量的複值函數。如果你不适應複分析，你可以把變量s看作一個實變量，因為這不會影響這些計算。
根據這個定義，我們可以計算兩個狄利克雷級數的乘積來得到這個結果：
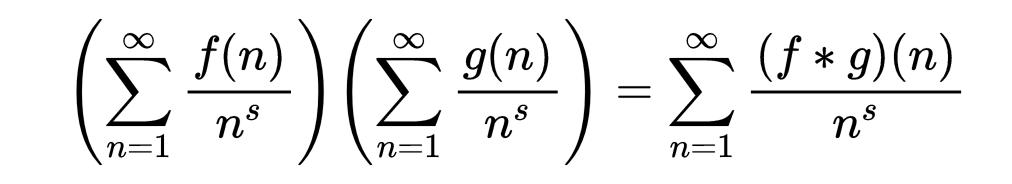
狄利克雷級數的一個非常著名的例子是這個級數的算術函數是單位函數u。
在這種情況下，由于u(n) = 1，對于所有n，我們得到狄利克雷級數：
這是著名的黎曼ζ函數ζ(s)，對于 Re(s) > 1。
歐拉積
在17世紀，萊昂哈德·歐拉發現了一個驚人的關系。具體來說，他發現黎曼ζ函數可以寫成質數的無窮積。
這就是函數的歐拉乘積。結果如下：
設ℙ表示所有質數的集合，使ℙ={2,3,5,7,11，…}，則：
在我看來，這是數學中最美妙的事實之一。
事實證明，這确實是一個更普遍現象的特殊情況！具體來說，如果f是一個積性算術函數，那麼我們會得到一個驚人的結果：
右邊可以擴展為更少符号的格式，如：
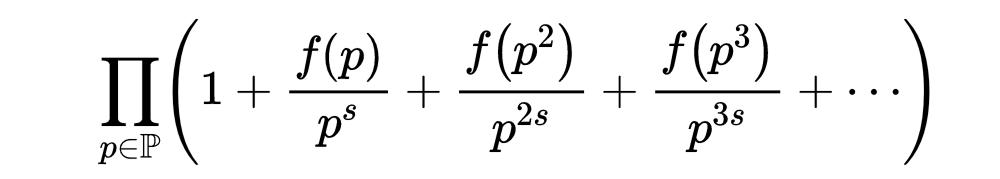
通過這個符号，不難看出為什麼是這樣。上面的左邊是所有自然數的和，所以每個m都應該以f(m)/m^s的形式出現。我們能從右邊證明嗎？
注意，如果m有質因數分解：
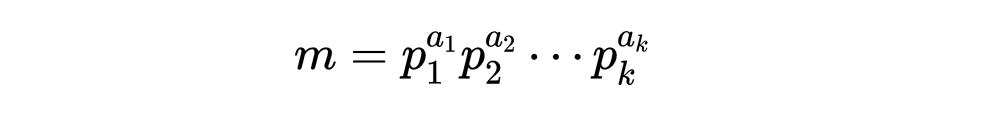
那麼：
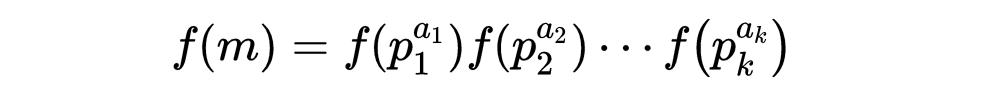
因為f是積性的。通過在右邊的質數乘積中選擇正确的項，我們就可以得到f(m)/m^s。我們可以對狄利克雷級數中的任何一項這樣做，這本質上是算術的基本定理。
上述結果也稱為歐拉積。現在回想一下幾何級數及其封閉形式：如果|x| < 1，那麼：
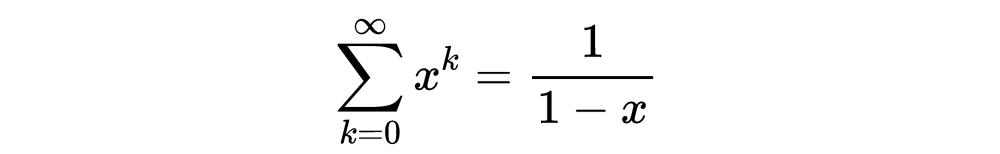
再加上如果一個算術函數f是完全積性的，即f(nm) = f(n)f(m)對于所有的n，那麼f(p^k) = f(p)^k。因此，上面的歐拉乘積在這種情況下有一個更簡單的表達式。利用在素數乘積的每個因子中出現的幾何級數的封閉表達式，完全積性函數的公式得到了以下值得注意的結果：
因為u是完全積性的，如果我們在上面的公式中用u代替f，我們就可以得到黎曼ζ函數的歐拉積！
一個應用
我們知道很多函數是積性的，所以可以通過它們的歐拉乘積來研究很多不同的狄利克雷級數。
以著名的莫比烏斯函數μ為例。因為μ是積性的，我們有：
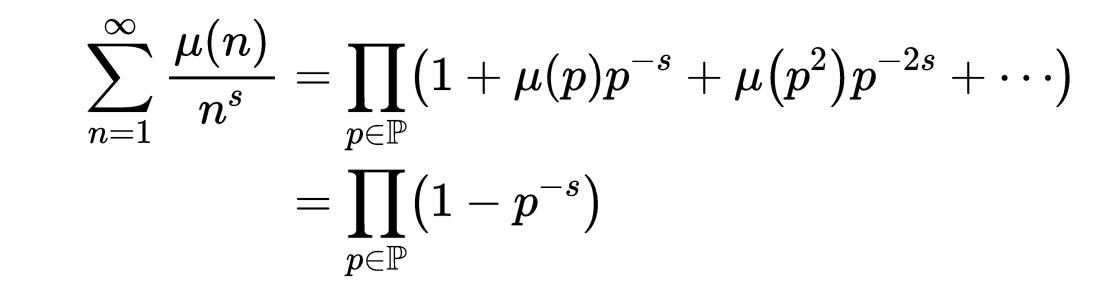
這裡最後一個等式成立因為當k≥2時，μ(p^k) = 0。
這讓你想起什麼了嗎？這幾乎就是黎曼ζ函數除了這個因子在分子上而不是分母上。事實上，我們剛剛展示的是：
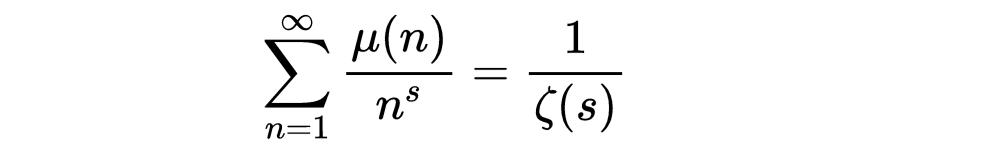
但是狄利克雷卷積在哪裡呢？有了上面的結果和莫比烏斯反演公式，我們可以做一些非常有趣的事情。
設g是一個算術函數，設f = g * u。
現在，考慮以下計算：
我們得出結論：
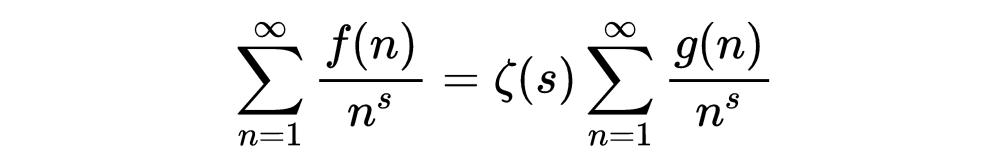
這是一個非常有趣的結果。ζ就像一個轉換器，在“除數求和”和對應的狄利克雷級數之間轉換。
一個直接的結論是：如果g(n) = n，即g = N，則上述公式給出了黎曼ζ函數和因子和函數σ之間的重要關系：
更多精彩资讯请关注tft每日頭條，我们将持续为您更新最新资讯!
zpostcode 
Recruit 
weather 
mreligion 
Yellowpages 
sport 
constellation 
shopping 
name 
game 
directory 
literature 
Word 
tour 
furnish 
Lottery 
tftnews 
lyrics 
News 
digital 
car 
dir 
Edu 
Finance 
