對多項式S分解因式：
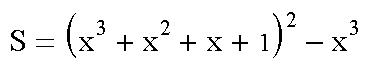
我們先回顧一下相關知識：
一、定義
把一個多項式在一個範圍化為幾個整式的積的形式，這種式子變形叫做這個多項式的因式分解，也叫做把這個多項式分解因式。
因式分解是中學數學中最重要的恒等變形之一，它被廣泛地應用于初等數學之中，在數學求根作圖、解一元二次方程方面也有很廣泛的應用，是解決許多數學問題的有力工具。
二、方法
因式分解主要有十字相乘法，待定系數法，雙十字相乘法，對稱多項式，輪換對稱多項式法，餘式定理法等方法，求根公因式分解沒有普遍适用的方法，初中數學教材中主要介紹了提公因式法、運用公式法、分組分解法。而在競賽上，又有拆項和添減項法式法，換元法，長除法，短除法，除法等。
三、基本步驟：
(1)找出公因式；
(2)提公因式并确定另一個因式；
四、口訣：
口訣：找準公因式，一次要提盡，全家都搬走，留1把家守，提負要變号，變形看奇偶。
我們回到題目：
第一步，分析
題目中S包含有多項式的平方，和三次項，如果直接開平方出來的話，将産生六次項，分解難度增大，計算量将無法估計不是好辦法。考慮平方就會聯想到平方差公式，考慮立方就會聯想到立方差和立方和公式，分解後，預計會産生公因子，按此思路我們進行配系數，得到：
按平方差公式分解因式，按立方差分解因式，都是基本公式，沒有難度，直接寫出代數式即可：
整理化簡後，得到：
發現，确實存在公因子，可以提取公因子，提取公因子後得到：
整理化簡後得到：
兩個乘積項在實數範圍内已經不能再因式分解了，上式即為最終答案。
,更多精彩资讯请关注tft每日頭條，我们将持续为您更新最新资讯!
zpostcode 
Recruit 
weather 
mreligion 
Yellowpages 
sport 
constellation 
shopping 
name 
game 
directory 
literature 
Word 
tour 
furnish 
Lottery 
tftnews 
lyrics 
News 
digital 
car 
dir 
Edu 
Finance 
