前提條件：度量随機性的新方法。

到目前為止，我們講的和概率有關的随機試驗都是獨立的，即前後不相關。但是世界上很多随機事件的發生是彼此相關的，比如今天的天氣就和昨天的天氣有關；在一句話中，某個詞是否出現，和上一個詞不僅相關，而且關系極大。同樣一個随機事件，在不同條件下發生的概率，差異是巨大的，因他們用一種新的度量随機性的方法，将随機事件發生的條件也考慮進去。

一、前提條件：條件對随機性的影響。

概率确定的随機事件，在不同條件下發生的可能性常常會有巨大的變化，我們不妨先來看一個真實的例子，體會一下條件對概率的影響。

1.被哈佛大學錄取的概率問題和中國大學完全看分數錄取不同，美國頂級私立大學的錄取有很大的随意性，因為平時成績(從九年級到十二年級第一學期的平均分)和标準考試成績，隻不過是被考察的十多個維度中的兩個維度而已，其他的維度有一大半是主觀的，比如學生性格可能對其學生帶來的益處，這完全依照審核材料的人的主觀判斷，在中國，像清華北大這樣的名校錄取時有很大的确定性一一你少一分也不行，但是在美國，像哈佛這樣的大學，能否錄取幾平就是一個随機事件。美國甚至有這樣的笑話，說哈佛負責錄取的工作人員頭一天晚上把該錄取學生的材料在了一起，把該拒絕學生的材料放在了另一邊，但是沒有做标識，到了第二天，他完全分不清哪一些是該錄取學生的材料了。這雖然是一個笑話，但說明了錄取過程中的随機性。那麼被哈佛錄取這個随機事件發生的概率是多少呢?2009到2019年的10年間，這個概率在5%一6%浮動一一每年錄取的人數基本上是常數，但是分母，也就是申請者人數變化較大。

接下來的問題是，一所一流的高中(類似中國的重點高中)的某個學生申請哈佛，是否有5%左右的機會被錄取呢?或是說有100個學生申請哈佛，是否會有5個左右的學生被錄取呢：答案看條件而定。各種影響錄取結果的條件，至少可以分為三個維度。

首先，要看100個學生是提前申請還是正常申請。

美國絕大部分名校允許學生報一所提前申請的大學(稱為EA或者ED，通常在11月底之前要完成申請)。比如，你可以提前申請哈佛。或者耶魯，但是不能同時申請這兩所學校。當然，對于正常申請(簡稱RA)則沒有限制，你愛申請多少所就申請多少。2019年哈佛一共錄取了1950名學生，錄取率隻有4.5%(43330人申請)，這是它的曆史最低水平。但是，提前申請的人，錄取率則高達13.4%(6958名提前申請者中的935人被錄取)。顯然要高得多。在3632名正常申請者中，隻錄取了1015人，錄取率隻有2.8%。也就是說如果提前申請，被錄取的概率要比正常申請高将近4倍。為什麼美國大學喜歡招收提前申請者呢，因為在美國，每一個學生可能會同時被很多所大學錄取，而他隻能接受一所大學的錄取，剩下的全作廢，這樣就白白浪費了大學寶貴的錄取名額。而提前申請，一且被錄取後，大部分學生會接受錄取通知書(有些大學會要求學生必須接受，并且自動終止其他大學的申請過程)，放棄申請其他大學。

這樣學校能保證錄取一人來一人。因此，美國所有的名校，提前請者的錄取率都要比正常申請者的高得多。

如果把被(哈佛)錄取這個随機事件用A來表示，提前申請這件事用B來表示，當然，正常申請對應的就是:

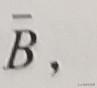
，我們已經知道A發生的概率P(A)=4.5%，提前申請者被錄取的概率，就是在B這個條件下，事件A發生的概率等于13.4%，我們把它寫成P(AlB)=13.4%，類似地，在B不發生的條件下，事件A發生的概率等于28%,即:

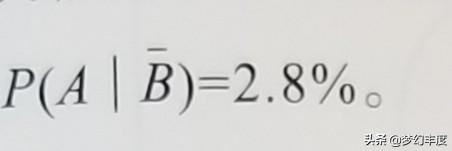
回到前面的問題，如果那所中學100名申請者都是提前申請，應該會有5個甚至更多的學生被哈佛錄取。但如果是正常申請，通常被錄取的人會少于5人，甚至可能一個都沒錄取。從這個例子可以看出，在不同條件下，一個随機事件發生與否，概率會差很大。

其次，要看“是否為特定校友的孩子”。條件概率的條件可以有很多種，比如哈佛等大學一直會照顧特定校友2的子女，根據全國公共廣播電台(NPR)的報道，這群學生被錄取的概率接近34%(2009—2015年)，而同時期總的錄取概率隻有5.9%，差出5倍左右。我們假設這個條件為C.根據全國公共廣播電台的說法，我們可以得到這樣的結論：

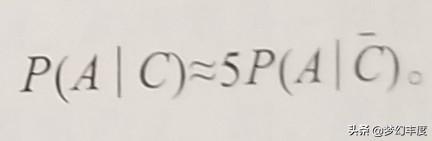
也就是說，如果我們前面說的高中有學生的父母都是哈佛畢業生，那麼100個申請者被錄取5個是非常有可能的，否則，可能性其實很小。事實上，矽谷地區有一所高中，很多學生都是斯坦福校友的孩子，這所高中的學生每年被斯坦福錄取的人非常多，是被其他名校錄取的人的好幾倍。

再次，要看學校的地理位置，這個條件我們後面再分析。

通過對上述兩個條件的分析，我們已經看出要想對一個随機事件發生的概率作出準确的估計，就需要考慮它發生的各種條件。

今天我們大部分人說到概率時，都是泛泛地在談可能性，而沒有細地考慮各種條件，以至于自己的感覺和結果會相差甚遠。很多人至會覺得明明是大概率的事件卻沒有發生，小概率的事件卻經常發生。這其實是忽略了條件的結果。

2.條件概率的計算公式。

既然條件概率很重要，那麼怎麼計算條件概率呢?我們不始回顧一下上一章中所講到的對概率估算的方法，即用一個随機事件A發生的次數#(A)，除以總的試驗次數#。

根據大數定理，當#足夠大的時候，#(A)/#→P(A)。在統計中，通常會将#(A)/#稱為随機事件A發生的相對頻率，記做f(A)。我們通常會認為P(A)=f(A)當#足夠大之後，我們有時也簡單地寫成：

P(A)=f(A)=#(A)/#。式1.

在計算條件概率P(A|B)時，我們要考慮當條件B發生了#(B)之後，随機事件A在B發生的條件下發生了多少次，我們假定它為叫#(A，B)次。于是，我們可以把#(A，B)/#(B)定義成條件B下A發生的相對頻率f(A|B).當#(A，B)足夠大的時候，就有：

P(AIB)=f(Al B)=#(A, B)/#(B) 式2

在前面的例子中，被哈佛提前錄取的人數935就是#(A，B),而提前申請的人數6958，就是#(B)，它們的比值，就是條件概率P(A\B)。#(A)，#(B)、#(A，B)和總數#的關系，我們可以用下圖來表示。

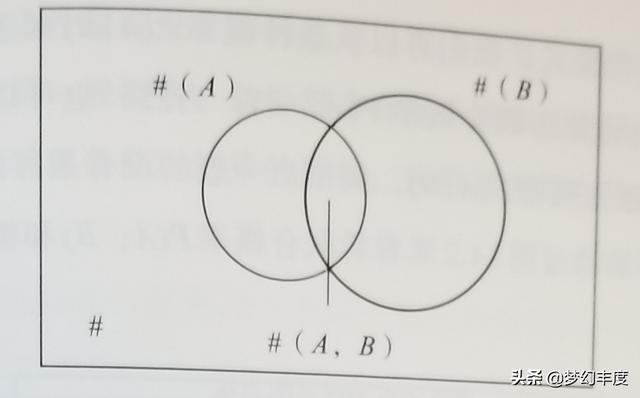
圖1

上圖樣本總數樣#、随機事件發生的次數就是#(A)、條件發生的次數是#(B)以及條件和随機事件同時發生的次數#(A，B)之間的關系。

如果我們把式(2)的右邊分子和分母同時除以樣本總數就得到下面的等式:

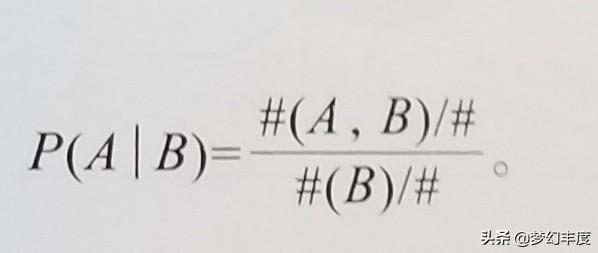
式3

分母#(B)/#，B本身的概率P(B)，而分子#(A，B)/#=則是一種新的概率一一随機事件A和條件B和同時出現的概率P(A，B)，我們稱之為A和B的聯合概率分布。于是，式(2)就可以重寫成

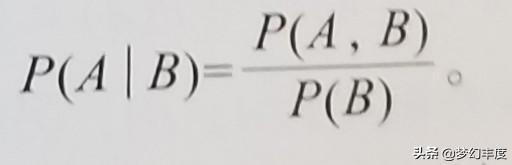
式4

這個公式其實才是條件概率原本的計算公式，隻是它不如式(2)形象，不容易理解，因此從(2)推導出(4)。

現在，對于一個随機事件A，我們有了三種概率：沒有任何限制條件一般意義上的概率P(A)，它在條件B發生後才發生的條件概率P(AlB)，以及它和B一同出現的聯合概率P(A，B)，這三種概率彼此是有聯系的，我們通常可以其中兩種得到第三種，比如我們将式(4)換一種方式表述，就得到下面的公式

P(A,B)=P(AIB)*P(B)。 式5

利用這個公式，我們可以從條件概率P(AlB)和條件本身發生的概率P(B)計算出聯合概率P(A，B)；當然，也可以從聯合P(A，B)和條件概率P(AlB)，倒推出一般的沒有條件的概率P(A)。

我們不妨通過下圖來看看聯合概率P(A，B)和概率PA之的關系。

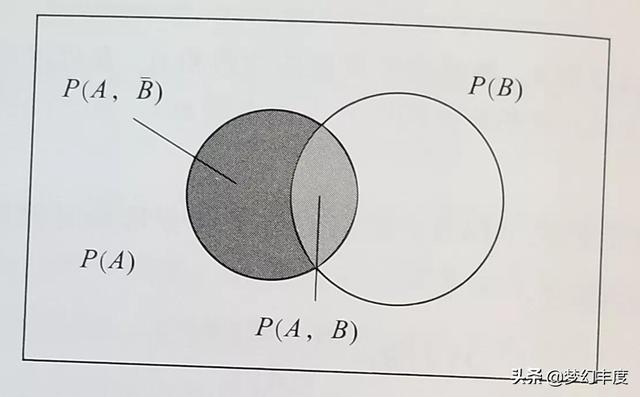
圖2

圖中概率P(A)，條件的概率P(AlB)，以及聯合概率P(A,B)的關系。

圖2中随機事件A發生的概率P(A)其實包含兩部分：一部分是A和B同時發生下的聯合概率P(A，B)，另一部分是A發生了但是B沒有發生的概率:

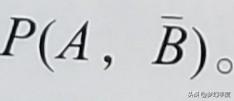
。由此我們可以得到下面的等式:

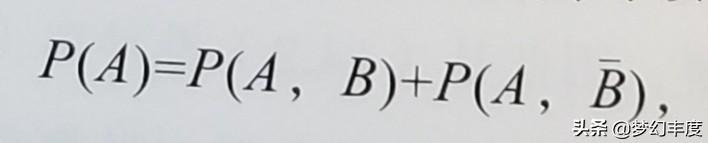
式6

這就從聯合概率分布得到一般的概率分布。接下來，我們将式(5)和式(6)合并，就得到概率和條件概率之間關系式:

式7

上述兩個公式警示我們在使用概率時，不能将某個條件下發生的概率和一般的概率相混淆，因為前者隻是後者的一部分，而後者還包括那個條件沒有發生時的概率。在下一節，我們将通過一些實例進一步說明一般概率、條件概率和聯合概率的差異。從這些例子中大家可以看到條件對結果的影響，這樣就清楚在什麼場合該用什麼概率了。

本節思考題:

一個人的某種生理指标A檢測如果呈陽性，這個人可能染上了一種疾病B，某醫院檢測了1000個人，有240個人的檢測結果呈陽性。經過進一步确認，這1000個人中有160個人患了疾病B，其中有150個人指标A的檢測結果呈陽性。請問:

1.如果某個人檢測結果為陽性，他其實沒有染病的概率是多少?

2.如果某個人的檢測結果為陰性，他其實染病的概率是多少?

更多精彩资讯请关注tft每日頭條，我们将持续为您更新最新资讯!