如果問初一學生有理數哪部分内容最難，相信很多學生會回答，絕對值！今天讓我們一起梳理絕對值的知識點和解題方法，幫學生輕松攻克絕對值！

絕對值有兩個意義：

（1）代數意義：非負數（包括零）的絕對值是它本身，負數的絕對值是它的相反數。即|a|＝a（當a≥0） , |a|＝－a （當a＜0）

（2）幾何意義：一個數的絕對值等于數軸上表示它的點到原點的距離。

靈活應用絕對值的基本性質：

（1）|a|≥0；（2）|ab|＝|a|·|b|；（3）|a/b|＝|a|/|b|(b≠0)（4）|a|－|b|≤ |a＋b|≤|a|＋|b|；（5）|a|－|b|≤ |a－b|≤|a|＋|b|；

點A、B在數軸上分别對應的數為a、b，則A、B兩點間的距離表示為|AB|＝|a－b|，利用絕對值的距離公式找最小值，是考試中的一個難點。現在跟随老師的腳步，從特色到一般出發，一起探究做此題的套路吧，這一類題就都可以解決啦！

【問題提出】|a﹣1| |a﹣2| |a﹣3| … |a﹣2019|最小值是多少？

【閱讀理解】

為了解決這個問題，我們先從最簡單的情況入手．|a|的幾何意義是a這個數在數軸上對應的點到原點的距離．那麼|a﹣1|可以看做a這個數在數軸上對應的點到1的距離；|a﹣1| |a﹣2|就可以看作a這個數在數軸上對應的點到1和2兩個點的距離之和．下面我們結合數軸研究|a﹣1| |a﹣2|的最小值．

我們先看a表示的點可能的3種情況，如圖所示：

（1）如圖①，a在1的左邊，從圖中很明顯可以看出a到1和2的距離之和大于1．

（2）如圖②，a在1和2之間（包括在1，2上），可以看出a到1和2的距離之和等于1．

（3）如圖③，a在2的右邊，從圖中很明顯可以看出a到1和2的距離之和大于1．

【問題解決】

（1）|a﹣2| |a﹣5|的幾何意義是______．請你結合數軸探究：|a﹣2| |a﹣5|的最小值是_____．

（2）|a﹣1| |a﹣2| |a﹣3|的幾何意義是_____．請你結合數軸探究：|a﹣1| |a﹣2| |a﹣3|的最小值是 ______，并在圖④的數軸上描出得到最小值時a所在的位置，由此可以得出a為 ______．

（3）求出|a﹣1| |a﹣2| |a﹣3| |a﹣4| |a﹣5|的最小值．

（4）求出|a﹣1| |a﹣2| |a﹣3| … |a﹣2019|的最小值．

【拓展應用】

請在圖⑤的數軸上表示出a，使它到2，5的距離之和小于4，并直接寫出a的範圍．

【分析】（1）根據絕對值的幾何意義結合數軸即可求解；

（2）由題意可得出，取中間值a＝2時，求得最小值；

（3）由題意可得出，取中間值a＝3時，求得最小值；

（4）由題意可得出，取中間值a＝1010時，求得最小值．

【解答】（1）|a﹣2| |a﹣5|的幾何意義是a這個數在數軸上對應的點到2和5兩個點的距離之和；

當a在5和2之間時（包括在5，2上），

可以看出a到5和2的距離之和等于3，

此時|a﹣2| |a﹣5|取得最小值是3；

故答案為：a這個數在數軸上對應的點到2和5兩個點的距離之和；3．

（2）|a﹣1| |a﹣2| |a﹣3|的幾何意義是a這個數在數軸上對應的點到1、2和3三個點的距離之和．

當a取中間數時，絕對值最小，|a﹣1| |a﹣2| |a﹣3|的最小值是1 0 1＝2；

如圖所示：

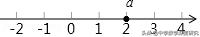
故答案為：a這個數在數軸上對應的點到1、2和3三個點的距離之和；2；2．

（3）當a取中間數3時，絕對值最小，

|a﹣1| |a﹣2| |a﹣3| |a﹣4| |a﹣5|的最小值是：2 1 0 1 2＝6．

（4）當a取中間數1010時，絕對值最小，

|a﹣1| |a﹣2| |a﹣3|… |a﹣2019|的最小值為：

1009 1008 1007 … 1 0 1 2 3 … 1009＝1009×（1009 1）＝1019090．

【點評】此題主要考查了絕對值的性質，解這類問題的基本步驟是：求零點、分區間、定性質、去符号、即令各絕對值代數式為0，得若幹個絕對值為零的點，這些點把數軸分成幾個區間，再在各區間内化簡求值即可．

牛刀小試：

上面的例題你學會了嗎？那麼我們來挑戰一下自己吧！

1、若|a|＝a＋1，|x|＝2ax，且|x＋1|＋|x－5|＋2|x－m|的最小值是7，則m等于多少？

2、如圖，一條街道旁有五幢居民樓．某大桶水經銷商統計各樓居民每周所需大桶水的數量如下表：

他們計劃在這條街道上租賃一間門市房，設立大桶水供應點．若僅考慮這五幢樓内的居民取水所走路程之和最小，可以選擇的地點應在什麼地方？

【反思】理解絕對值的幾何意義是關鍵．結合數軸求兩點之間的距離，形象直觀，滲透數形結合的思想．求x到n個點距離和的最小值總結：（1）如果有奇數個點，當動點處在最中間那個點的位置時，它到所有點的距離之和最小。（2）如果有偶數個點，當動點處在最中間的兩個點之間時，它到所有點的距離之和最小。用一句話來記憶，就是奇中偶範。即奇數個點時，取最小值是在最中間的點。偶數個點時，取最小值是在最中間的兩個點之間的範圍内都可以。

常用解題方法：（1）化簡絕對值：分類讨論思想（即取絕對值的數為非負數和負數兩種情況）；（2）運用絕對值的幾何意義：數形結合思想，如絕對值最值問題等。（3）零點分段法：求零點、分段、區段内化簡、綜合。

希望孩子們通過此次對絕對值的學習能夠逐漸形成分類讨論的思想，利用數形結合等方法慢慢培養自己的觀察、模仿、總結的能力，在新初一有個好的開始喲。

更多精彩资讯请关注tft每日頭條，我们将持续为您更新最新资讯!