一.知識框架圖
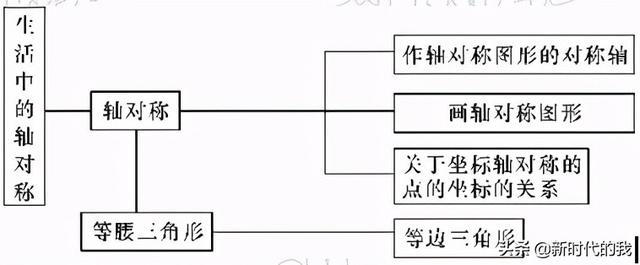
二.軸對稱和軸對稱圖形
1、有一個圖形沿着某一條直線折疊，如果它能夠與另一個圖形重合,那麼就說這兩個圖形關于這條直線對稱，這條直線叫做對稱軸，折疊後重合的點是對應點，叫做對稱點．兩個圖形關于直線對稱也叫做軸對稱．
2、軸對稱圖形：如果一個圖形沿一條直線折疊，直線兩旁的部分能夠互相重合，這個圖形就叫做軸對稱圖形。這條直線就是它的對稱軸。（對稱軸必須是直線）
3、對稱點：折疊後重合的點是對應點，叫做對稱點。
4、軸對稱圖形的性質：如果兩個圖形關于某條直線對稱，那麼對稱軸是任何一對對應點所連線段的垂直平分線。類似的，軸對稱圖形的對稱軸，是任何一對對應點所連線段的垂直平分線。連接任意一對對應點的線段被對稱軸垂直平分．軸對稱圖形上對應線段相等、對應角相等。
5．畫一圖形關于某條直線的軸對稱圖形步驟：找到關鍵點，畫出關鍵點的對應點，按照原圖順序依次連接各點。
三.軸對稱與軸對稱圖形的區别和聯系
區别：軸對稱是指兩個圖形之間的形狀與位置關系，成軸對稱的兩個圖形是全等形；軸對稱圖形是一個具有特殊形狀的圖形，把一個軸對稱圖形沿對稱軸分成兩個圖形，這兩個圖形是全等形，并且成軸對稱．
聯系：1：都是折疊重合 2;如果把成軸對稱的兩個圖形看成一個圖形那麼他就是軸對稱圖形，反之亦然。
線段的垂直平分線
經過線段的中點并且垂直于這條線段的直線，叫做這條線段的垂直平分線（或線段的中垂線）
（2）線段的垂直平分線上的點與這條線段兩個端點的距離相等；反過來，與一條線段兩個端點距離相等的點在這條線段的垂直平分線上． （證明是必須有兩個點）因此線段的垂直平分線可以看成與線段兩個端點距離相等的所有點的集合．
四.用坐标表示軸對稱
1、點（x，y）關于x軸對稱的點的坐标為（-x，y）
2、點（x，y）關于y軸對稱的點的坐标為（x，-y）；
五.關于坐标軸夾角平分線對稱
點P（x，y）關于第一、三象限坐标軸夾角平分線y＝x對稱的點的坐标是（y，x）
點P（x，y）關于第二、四象限坐标軸夾角平分線y＝－x對稱的點的坐标是（－y，－x）
六.關于平行于坐标軸的直線對稱
點P（x，y）關于直線x＝m對稱的點的坐标是（2m－x，y）；
點P（x，y）關于直線y＝n對稱的點的坐标是（x，2n－y）；
歡迎關注中學高分寶典
,更多精彩资讯请关注tft每日頭條，我们将持续为您更新最新资讯!
zpostcode 
Recruit 
weather 
mreligion 
Yellowpages 
sport 
constellation 
shopping 
name 
game 
directory 
literature 
Word 
tour 
furnish 
Lottery 
tftnews 
lyrics 
News 
digital 
car 
dir 
Edu 
Finance 
