幫幫有話說：為了高三備考的孩子，幫友帶來【高考專題】系列學習幹貨，該專題會準時發布針對一個科目一個知識點的幹貨内容，和高中幫友一起備戰高考！有需要的家長可以點擊作業幫，收藏本文并持續關注哦~

本期内容是高考專題Vol.05—數學：三角函數圖像與性質的四類考點。

下面，就為大家帶來最無聊，最枯燥但是最能提分，最有收獲的高考專題分享！

三角函數的有關知識大部分是B級要求，隻有函數y＝Asin(ωx＋φ)的圖象與性質是A級要求；

試題類型可能是填空題，同時在解答題中也是必考題，經常與向量綜合考查，構成中檔題。

1．記六組誘導公式

對于“π/2±α，k∈Z的三角函數值”與“α角的三角函數值”的關系可按下面口訣記憶，奇變偶不變，符号看象限．

2．正弦、餘弦、正切函數的圖象與性質(下表中k∈Z)

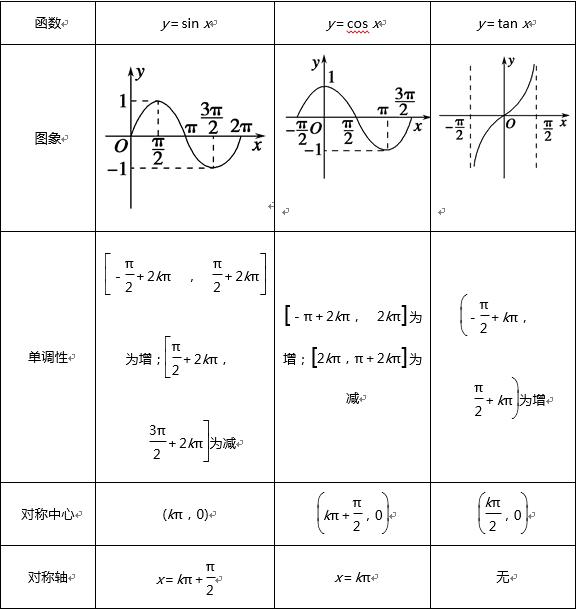
3.y＝Asin(ωx＋φ)的圖象及性質

(1)五點作圖法：五點的取法，設X＝ωx＋φ，X取0，π，2π來求相應的x值、y值，再描點作圖

(2)給出圖象求函數表達式的題目，比較難求的是φ，一般是從“五點法”中的第一點作為突破口．

(3)在用圖象變換作圖時，一般按照先平移後伸縮，但考題中也有先伸縮後平移的，無論是哪種變形，切記每個變換總對字母x而言

(4)把函數式化為y＝Asin(ωx＋φ)的形式，然後用基本三角函數的單調性求解時，要注意A，ω的符号及複合函數的單調性規律：同增異減

4．三角函數中常用的轉化思想及方法技巧

(1)方程思想：sin α＋cos α，sin α－cos α，sin αcos α三者中，知一可求二．

(2)“1”的替換：sin2α＋cos2α＝1

(3)切弦互化：弦的齊次式可化為切.

1．結合誘導公式與同角基本關系式化簡求值的策略

(1)切弦互換法．

利用tan α＝進行轉化．

(2)和積轉化法．

利用(sin α±cos α)2＝1±2sin αcos α進行變形、轉化．

(3)常值代換法．

其中之一就是把1代換為sin2α＋cos2α.

同角三角函數關系sin2α＋cos2α＝1和tan α＝聯合使用，可以根據角α的一個三角函數值求出另外兩個三角函數值．根據tan α＝可以把含有sin α，cos α的齊次式化為tan α的關系式．

2．化簡求值時的“三個”防範措施

(1)函數名稱和符号．

利用誘導公式化簡求值時，先利用公式化任意角的三角函數與銳角的三角函數，其步驟是：去負—脫周—化銳—求值．特别注意解題過程中函數名稱和符号的确定．

(2)開方．

在利用同角三角函數的平方關系時若需開方，特别注意要根據條件進行讨論取舍．

(3)結果整式化．

解題時注意求值與化簡的最後結果一般要盡可能化為整式．

題型1 三角函數的概念、誘導公式及基本關系式的應用

題型2 三角函數的圖像

題型3 三角函數的性質及其應用

題型4 求三角函數的解析式

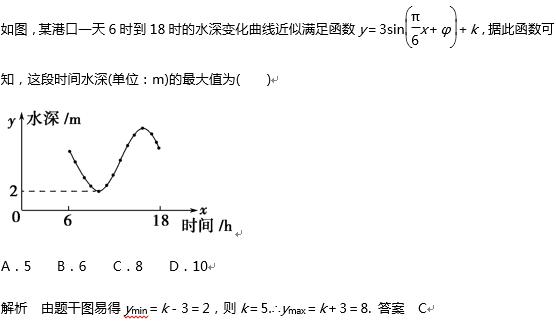
題型5 函數y=Asin（ωx＋φ）的綜合應用

以上内容是關于【三角函數圖象與性質】的考綱、重難點、知識拓展、經典題型的學習幹貨内容，如果你還想看關于本專題，點擊關注作業幫，分享更多教育知識~

更多精彩资讯请关注tft每日頭條，我们将持续为您更新最新资讯!