奇函數和偶函數相加是什麼函數?一、奇函數定義：一般地，對于函數f（x），如果對于函數定義域内任意一個x，都有f（-x）=-f（x）,那麼函數f（x）就叫做奇函數，現在小編就來說說關于奇函數和偶函數相加是什麼函數?下面内容希望能幫助到你，我們來一起看看吧!

奇函數和偶函數相加是什麼函數

一、奇函數定義：一般地，對于函數f（x），如果對于函數定義域内任意一個x，都有

f（-x）=-f（x）,那麼函數f（x）就叫做奇函數。

結論：①f（-x）=-f（x），

奇函數圖像關于原點對稱

奇函數定義域關于原點對稱

②奇函數f（x）在x=0處有意義時（即定義域包含0時），有f（0）=0

③奇函數f（x）的最大值與最小值之和為0。

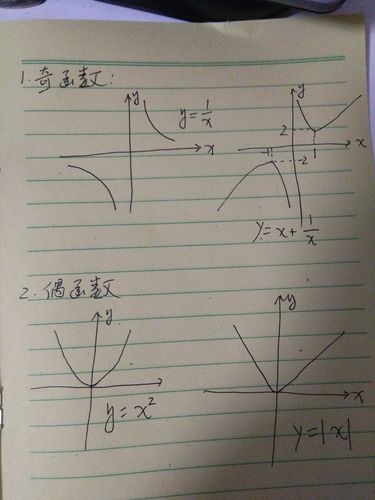
④常見奇函數：

⑤重要結論：已知函數g（x）為奇函數，a為常數，

f（x）=g（x） a，則有

M m=f（x） f（-x）=f（x₀） f（-x₀）=2a=2f（0）

其中M表示最大值，m表示最小值

二、偶函數

定義：一般地，對于函數f（x），如果對于函數定義域内任意一個x，都有

f（-x）=f（x）,那麼函數f（x）就叫做偶函數。

結論：①f（-x）=f（x）=f（l x丨）

偶函數圖像關于y軸對稱

偶函數定義域關于原點對稱

②定義域關于原點對稱的非零常函數是偶函數。

③若f（x）=ax² bx c（a≠0）為偶函數，則b=0

④重要結論：

Ⅰ已知偶函數f（x）在[0, ∝）上單調遞增，且f（x₁）>f（x₂），則有|x₁|>|x₂|

Ⅱ已知偶函數f（x）在[0, ∝）上單調遞減，且f（x₁）>f（x₂），則有|x₁|<|x₂|

三、奇、偶結論

①在公共對稱定義域内：兩個奇函數之和為奇函數，其積為偶函數；兩個偶函數之和與積都為偶函數；奇函數與偶函數之積為奇函數。奇函數的偶數個積、商是偶函數；奇函數的奇數個積、商是奇函數。奇函數的絕對值為偶函數；偶函數的絕對值為偶函數。

即 奇±奇=奇，偶±偶=偶，奇×奇=偶，

偶×偶=偶，奇×偶=倚

|奇|=偶， |偶|=偶

②y=f（x）=0既是奇函數又是偶函數

③若f（x）是奇函數，則f'（x）是偶函數

若f（x）是偶函數，則f'（x）是奇函數

④奇函數在對稱的單調區間内有相同的單調性；偶函數在對稱的單調區間内有相反的單調性。

即函數f（x）為［-a,a］上的奇(偶)函數，且f（x）在［0,a］上單增（減），則f（x）在［-a,0］上單增(減)。

四、運用奇函數重要結論解題

由此可見：遇見此類題目（題目給你一個複雜的，長得像奇函數的函數，實質上卻是奇函數 常數的形式），運用2f（0）解題是最直接最簡單便捷的方法

五、運用偶函數重要結論解題

函數與偶函數的這兩個重要結論，高考考過多次，平常的考試與習題也經常遇見。

因此，請牢記結論，一起進步，加油！

更多精彩资讯请关注tft每日頭條，我们将持续为您更新最新资讯!