前面幾天的話題我接不下去了，今天轉台，寫個不是太複雜的内容
說起來，線性回歸這個東西我之前是寫過的，而且仔細算算的話恐怕還不止一次，但是到今天再回過頭去翻翻自己當時（大概兩個月前）寫的東西，感覺自己之前學的也好，用的也好，都還挺淺的——即使現在也深不到哪兒去
我特意去翻出了兩個月前頭回寫線性回歸時編的那個例子：
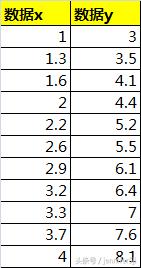
答案我也先放出來，以便後面檢查：
當時還挺自以為是的用了幾種不同的方式來做，但今天不啰嗦那麼多，就隻補充一種比較騷氣的計算方法——用數組和向量來計算線性回歸公式裡的系數（a和b）
公式就一個，是從書上來的：
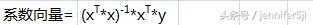
上标T表示矩陣行列轉置，對應Excel公式TRANSPOSE（行列位置交換）
上标-1表示矩陣求逆，對應Excel公式MINVERSE
請注意一個特殊的地方，由于整個公式是矩陣/向量級别的計算，所以裡面的乘号不是指一般的乘法，而是矩陣乘法公式MMULT，而且，更更更關鍵的部分是，矩陣乘法是不支持交換律的（也就是AxB不等于BxA），所以，計算乘法的順序從左到右一點都不能亂了——否則就會像我一樣公式打錯一卡住就半個多小時T-T
開始之前，還有點準備工作要做，那就是去平均值（x列y列各自減掉它們的平均值）
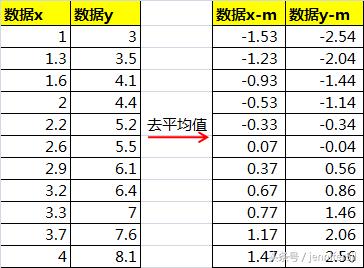
為什麼咧？因為書上用的這個公式是基于一個假設推導出來的，這個假設為：
y向量= 系數向量T * x向量
發覺沒，這裡面沒有常數項b，也可以說，它假設了b=0，解釋得再完整點，就是假設拟合出來的直線100%經過坐标原點(0,0)
所以，不要太着急，在這裡做去平均值還是非常有用的，因為它能幫我們把整個坐标的原點移到散點圖的中間，畫個圖給大家理解一下：
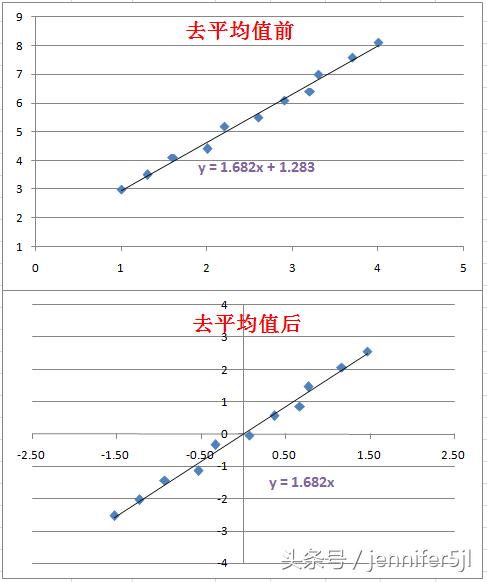
然後，按着公式做矩陣計算，這裡為了寫得簡單點，公式前面标識的x指的都是已經去平均後的x-m
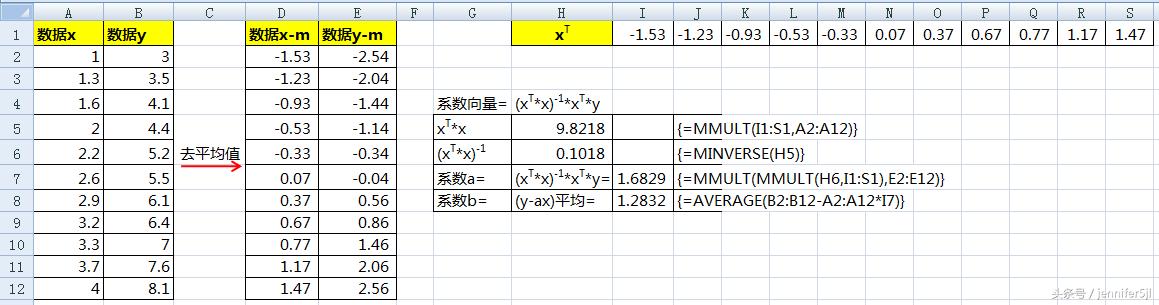
公式部分給大家放大一點：
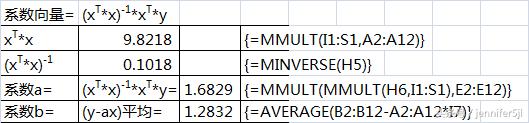
到這裡計算就結束了，但是，為什麼要用這麼麻煩的解法來計算一條直線呢？難道是吃飽了撐的？
當然不是，向量化的計算方法比其他一般的解法有一個最明顯的優勢——就是它支持同時有多列x的輸入值，像這樣：
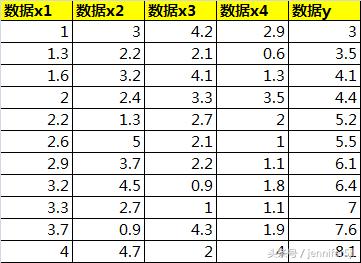
像這種情況下，Excel自帶的什麼畫圖啊，斜率截距公式什麼的肯定就廢了
例子都舉了（雖然是用随機數生成的），那就再做一個看看呗
公式形式：y=b a1x1 a2x2 a3x3 a4x4，走起
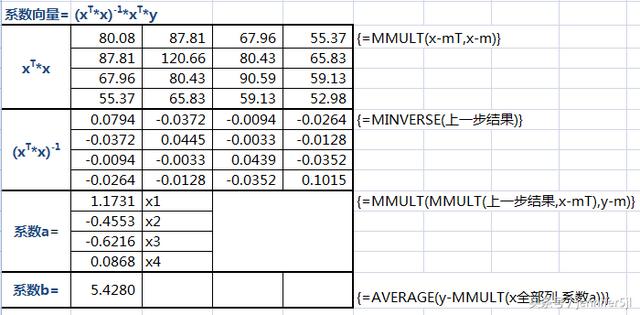
這樣是不是反而比正常的方式來得更簡潔了呢？
,更多精彩资讯请关注tft每日頭條，我们将持续为您更新最新资讯!
zpostcode 
Recruit 
weather 
mreligion 
Yellowpages 
sport 
constellation 
shopping 
name 
game 
directory 
literature 
Word 
tour 
furnish 
Lottery 
tftnews 
lyrics 
News 
digital 
car 
dir 
Edu 
Finance 
