初中幾何定值為常數4例
平面幾何中的定值問題,是指當點或線按照某種條件運動時,圖形發生位置、形狀或大小的變化,圖中的某些幾何元素的幾何量仍保持不變的情況。下面顯示幾例幾何定值為常數的例子。
題目1:如圖1,已知P為正方形ABCD的外接圓的劣弧上任意一點,求證(PA PC)/PB為定值。
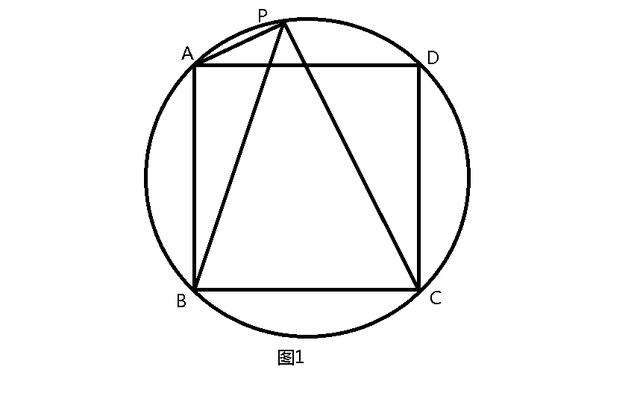
解題思路:見圖2,延長PC至E,使PA = EC,連接BE、AC。
方法①:因為 PA = EC,AB = BC,∠PAB = 90° α =∠ECB,故△PAB≌△ ECB。
PB = BE,∠PBE =∠P BC θ= 90°,R t△ PBE為等腰直角三角形。

PE /PB =√ 2 = (PC EC)/PB = (PA PC)/PB。
方法②:在圓内接四邊形ABCP中,應用托勒密定理證明相對簡單。
題目2:圖1,三角形ABC是等邊三角形,P是三角形ABC内任意一點,作三角形三邊的垂線
PD、PE、PF, 點D、E、F是垂足。證明:(PD PE PF) /(AB AC BC) =√3/6。

解題思路:①圖2,首先證明等邊三角形内任意一點P到三邊距離和等于一邊上的高,分别連接PA、PB、PC,并作BC邊上的高AG。
通過面積法可以證明AG = PD PE PF。
因為Rt三角形ABG中,∠BAG = 30°,
AG /BG =√3 =AG/(1/2 BC)。
BC = 1/3 (AB AC BC)。
AG/(1/2 BC)=(PD PE PF)/(1/2 BC)=√3,
(PD PE PF) /(AB AC BC) =√3/6。
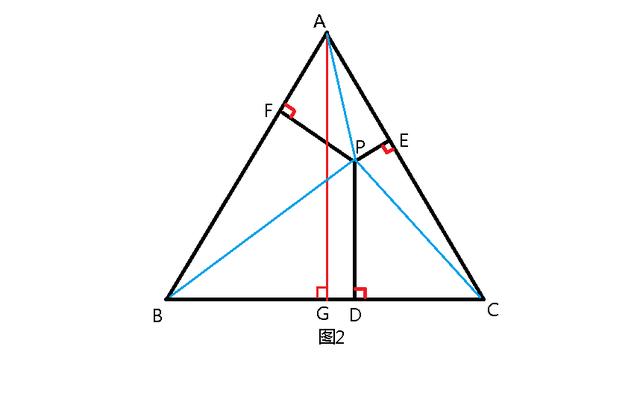
②根據等邊三角形的面積=√3/4 AB²,又等于P點與三個頂點相連形成三個三角形的面積和亦可證明。
題目3:如圖1,點0是正三角形ABC内一點,G是三角形ABC的重心,直線 0G與三角形ABC或其延長線分别相交于點A'、B'、 C',求證:A' O / A' G B' 0 / B' G C' 0 / C ' G = 3。
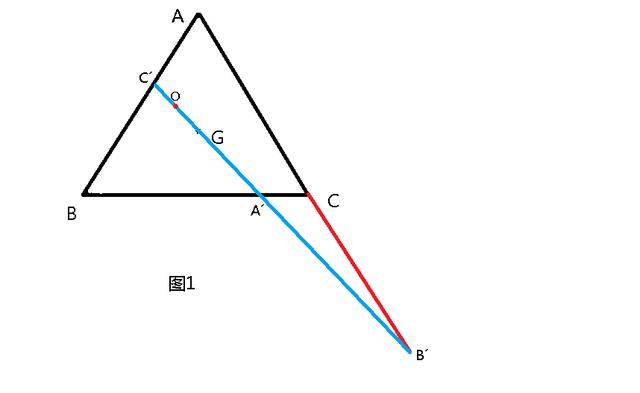
解題思路:先熟悉等邊三角形有幾個性質:等邊三角形重心、内心 、外心、垂心四心合一;等邊三角形内任意一點P到三邊距離和等于一邊上的高;重心到頂點的距離與重心到對邊中點的距離之比為2/1。
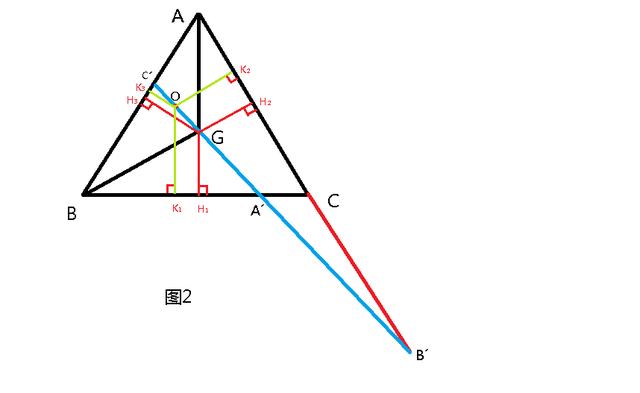
圖2中,設正三角形的高為H,分别過O點和G點作垂線OK₁、OK₂、OK₃和GH₁、GH₂、GH₃。則有:
OK₁ OK₂ OK₃=H,GH₁=GH₂=GH₃=1/3 H。
圖中有三組相似三角形,根據相似比顯示如下:
A' O/A' G B' 0/B' G C' 0 / C 'G
= OK₁/ GH₁ OK₂/ GH₂ OK₃/ GH₃
=( OK ₁ OK₂ OK₃)/ (1/3 H)
= H /( 1/3 H)
=3。
題目4:證明梅涅勞斯定理(梅氏定理):圖1,當一條直線交三角形ABC三邊所在的直線BC、AC、AB分别于點D、E、F時,則有AF /FB · BD /DC · CE / EA = 1。
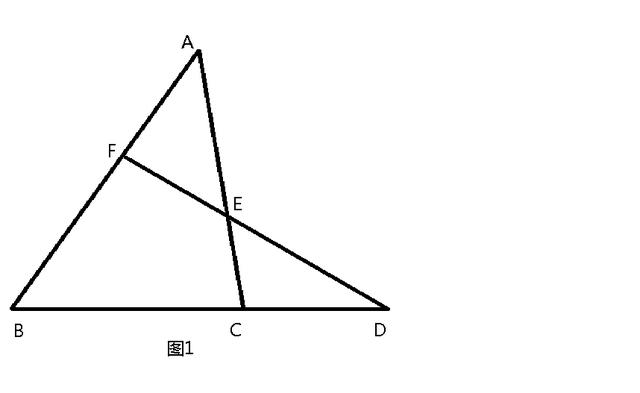
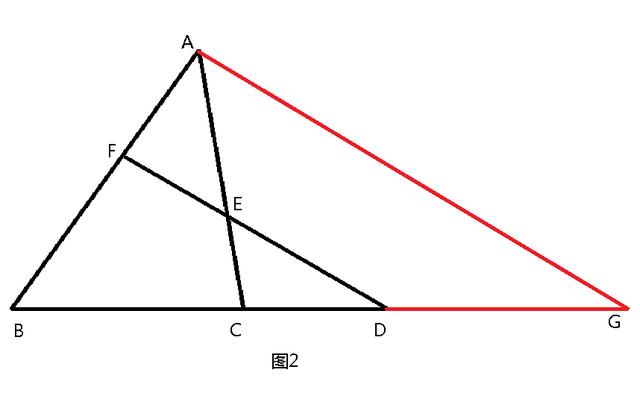
解題思路:見圖2,過A點作FD的平行線交BD延長線于G,則
AF /FB = GD /DB,
CE /EA = CD /DG,
所以AF /FB · BD /DC · CE /EA
= GD /DB · BD /DC · CD /DG = 1。
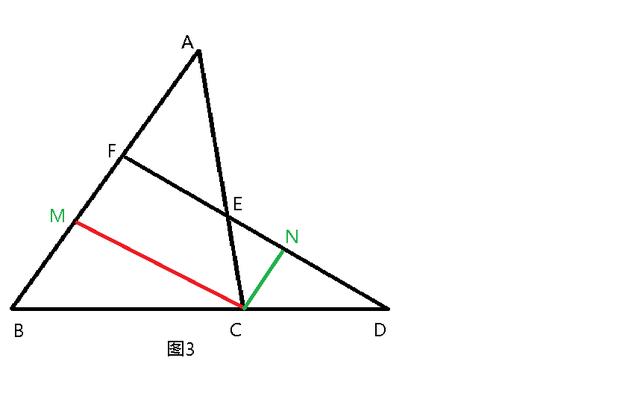
相同的方法見圖3,作CM∥FD或者CN∥AB亦可證明結論成立。
更多精彩资讯请关注tft每日頭條,我们将持续为您更新最新资讯!




