作者丨Thomas Viehmann

編譯丨錢磊

編輯丨陳彩娴

今天我想要與大家分享的是深度神經網絡的工作方式，以及深度神經與“傳統”機器學習模型的不同之處。我的計劃具體如下：

• 首先簡單地思考一下如何将問題設置成分類的形式；

• 接下來回顧偏差-方差分解，并在偏差-方差權衡的背景下，在VC-維數和非參數上進行探讨；

• 研究一些關于插值神經網絡和雙下降的文獻；

• 在文末做一個非常簡單的實驗，用圖形直觀地講解為什麼雙下降現象會發生。

1

正式設置一個機器學習問題

為了有些趣味，讓我們先設置一個問題。

首先從數據開始。假設我們标記了數據，即是滿足Px,y分布的輸入數據x（比如圖片）和标簽y。

如此一來我們得到：

分布Px,y固定且未知。對于i = 1……N來說，可獲得樣本

,

。

數學分析通常假設樣本是獨立的。

通常來說，我們需要假設标簽y和輸入x間有y=

的函數關系，即是說，标簽是精确的、沒有歧義的，但并非總是如此。我們想要“訓練”的是某些函數f:x↦y，或者說是更普遍地估計條件分布P(y∣x)。我們的候選函數來自于參數集F={fθ∣θ∈Θ}，在這裡θ代表參數。為了達成目标，我們設定了損失函數（或風險函數），從概念上講，我們希望将預期損失

最小化。

第一次嘗試通常是将經驗風險或者經驗損失

最小化。如果我們的損失函數是負對數似然，将

最最小化就意味着計算最大相似估計。

對偏差-方差分解和偏差-方差平衡的簡單介紹

中采得的随機變量，且我們訓練的模型 f依賴于D，記作

。通過巧妙地添加

并利用 (x,y) 和D的獨立性，我們可以将預測的期望平方誤差分解為：

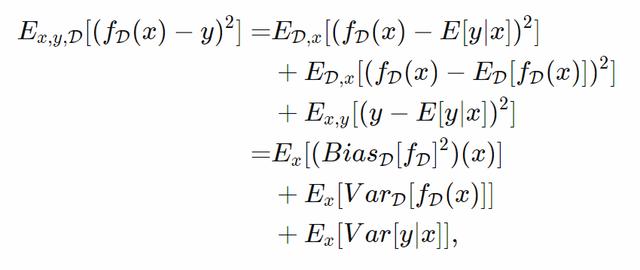
最後一項噪音并不依賴于我們的模型。

現在為了得到我們預測的良好的預期平方誤差，我們必須注意到模型輸出的偏差(第一項)和方差(第二項)的和很小。注意這裡所有的項都是非負的。

針對二元分類器的預期精度，其實存在着類似但更複雜的分解，但其他損失函數通常很難分解，盡管我們可以想象那樣的模型選擇的工作也是類似的。

因為讓偏差/方差等于0或非常接近0都相對容易，這樣分解會讓我們在偏差和方差間做出權衡：通過使用D中每個數據點的樣本均值作為估計，偏差可以非常小，且能巧妙地給出正則性論證來假設函數是Lipschitz函數或至少是一緻連續。這就是極端的過拟合。通過預測不依賴于D的函數，比如

，我們可以讓方差為0，這樣則是極端的欠拟合。

請注意，均方誤差的偏差-方差分解是一個根據數學定理(或至少一個引理)成立的方程，所以是普遍适用的，不需要任何條件。

2

從僵化中解脫出來，帶來自由的結構

從某種程度上說，從上述極端情況轉向更溫和的條件也表明了我們在實踐中可以做些什麼。

增加候選函數的集合

的大小或其VC維的項。此處的典型情況是，一個人想要N≥VC-dim個樣本，卻可能有N≤20VC-dim個樣本。但請注意，這裡參數的數量不是标準的一部分(但可能會影響VC維)。

最後，傳統标準比如赤池信息量準則嘗試告訴你應該“投資”多少參數來達到低的負對數可能性。但是Bishop在其引言中發現，這些方法并不是很有效。

非參數估計:正則化

裡有弱導數的索伯列夫函數空間

(無論采用何種測度，是x的分布抑或是包含輸入的

的勒貝格測度)，我們可以匹配任意有限樣本D上每一點的樣本均值，從而可以獲得0點态偏差, 但是最小化經驗風險是病态的，有無限多的解。

接下來要做的就是正則化。最著名的例子可能是增加一個規範項從而導緻Tikhonov正則化，所以我們的損失看起來會是這樣

如果我們從偏差-方差的角度來看，我們能夠平衡偏差（當λ→0沒有偏差，但會導緻病态）與方差（當λ→∞，我們處于

。我們并不想讓方差為0，因為我們的正則化項僅僅是一個半範數）。當然了，Grace Wahba有關正則化回歸的研究尤其與保持偏差-方差間的良好平衡相關，特别是與如何尋找到一個合适的λ值相關。通過觀察給定的λ，

的極小值

會有半範數值

，該值必然能在

中将經驗最小二乘損失(第一項) 最小化，就可以将前一節中的ansatz函數與嵌套空間Fi聯系起來。因此來自遞增權重序列

的遞減範數序列

就給到了我們嵌套的Ansatz空間。

許多流行的正則回歸方法(例如Lasso)适合這種類型的框架。

贊美VC界

讓我們講回VC 界，正式一點以便增強直覺。關鍵的概率界限是為了準确性(或者說0-1的風險)

我們來分析一下。外面部分稱“概率大于等于1−η”（我們還得更精确一點），此處我們覺得概率η太小了，這意味着我們所有的隻是一個概率界限，而不是一個“幾乎肯定”的保證。

内部的部分基本上是說，在全概率分布上的精度非常接近于在訓練集上的精度，也就是說在N變得非常大的時候，我們有一個差值趨于零的精确邊界。

從表面上看，這告訴了我們關于風險或準确性的信息，但是關于模型又說明了什麼呢? 在我看來，關鍵的信息是，我們的模型是如此嚴格，以至于我們可以看到測試集上發生的一切(或者更精确地說，在完整的Px,y分布上發生的一切)已經在訓練集中發生了。

貝葉斯放一邊

3

這告訴了我們深度學習的什麼?

當我們将model.parameters（這裡我用的是PyTorch）傳遞給優化器時，深度學習看起來好像是參數化的。但其實它不是!

看起來這種正則化方法正是深度學習運作的理論框架——有時人們對此知之甚少。我們的模型足夠大，從“道德上看來”足以成為非參數，盡管我們還沒有完全理解，但我們所做的大多數事情(比如augmentation, norm layers和 dropout)其實都是正則化。

這也是M. Belkin等人所寫的《協調現代機器學習實踐和偏差-方差權衡》(Reconciling modern machine learning practice and the bias-variance trade-off)的主題和他們早期研究的主題，即泛化性能的關鍵是由某個特定函數空間範數衡量的函數的規律性或平滑性。

我們有必要仔細看看M. Belkin等人(我認為這是首次)對雙下降現象的描述:

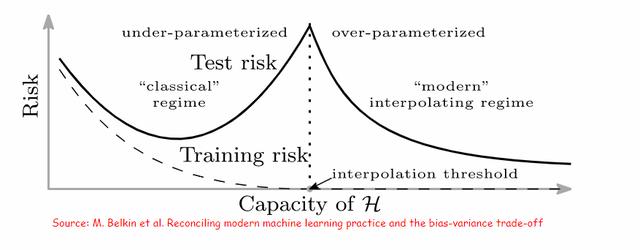
這裡有幾點需要注意:

• M. Belkin等人把條件中的“傳統(classical)”和“現代(modern)”等限定詞用引号括了起來。“現代”條件是一種十分之非參數的學習，具有一種我們還需要更加深入理解的正則化。

• 在多參數的條件下，偏差-方差思維似乎仍然是完全适用的，但非參數回歸可能是比“限制容量”的候選集更好的參考框架。

對于雙重下降現象的普遍理解似乎都是基于P. Nakkiran等人的文章:《雙重下降》(Deep Double Descent)，這證明了這篇論文的優秀，也證明了OpenAI能夠将這些選題推介給更廣泛的受衆。他們用更真實的網絡進行了系統的實驗(M. Belkin等人則引用了更淺層的網絡)。對我來說，一個重要的結論是，雙重下降現象在标簽損壞的兩種實驗條件中存在“凹凸”，他們的報告稱，在标簽幹淨的實驗中，所得到的結果則要平緩得多，沒有那麼“凹凸”。

他們給出了一張圖，這張圖顯示了對于固定次數的epoch，用損壞标簽将一個修改過的ResNet18訓練成CIFAR10這個過程中的測試錯誤。修改是指信道數量降到原數量的k分之一（k在64到1這個範圍）（意思是他們會從原ResNet18的64分之一開始做實驗，逐漸增加，最後達到原數量）。标簽損壞發生在數據集中(在某一次epoch，而不是每個epoch中)，15%的标簽被切換到一個随機錯誤的類。這被解釋為一種概略的誤設。

4

VC理論對于用噪聲标簽拟合模型有什麼啟示?通過上面的讨論，我們了解到當一個模型處于VC界有用的限定條件中（比如當小模型處于“傳統”條件中)，如果訓練數據 D來自與原始數據相同的分布Px,y，測試集的測試精度（很可能)接近訓練精度。換句話說，這個條件意味着我們假設Px,y有相同的損壞程度（和損壞種類)。但這意味着如果模型學習了，且學會了不被損壞的訓練數據分散太多注意力，也就是說，在訓練數據上，正确标簽會擠出損壞标簽。

5

特征和學習

讓對深度學習的直覺化變得困難的原因之一是Ansatz領域的自适應特性。我這麼說的意思是，我們沒有一個固定的特征提取器（由手動構造，并由核機中使用的核家族給出)将學習應用到特征上。通常，我們将最後一層的輸入視為特征（通過word2vet式損失、原型網絡、基準無監督學習等方式學習的向量表示方法)，或者我們可能在MLP分類器頭之前的卷積層末尾分割卷積網絡。

傳統的做法是将學習後的分類器放在固定的特征提取器上，E. Hoffer等人的想法卻相反，他們甚至建議對分類器進行固定，即隻對特征提取器進行訓練。

因此，我們可能會試圖通過假裝提取特征來簡化我們的直覺。在P. Nakkiran等人的标題圖片實驗中，當使用t-SNE等降維機制将通過無噪聲數據學習到的特征可視化時，添加标簽噪聲相當于在每個類對應的點的blob上添加噪聲。考慮到這一點，我們可以進行一個類似的實驗，這個實驗甚至比M. Belkin等人的人工數據實驗更簡單，那就是：理解深度學習。

6

對标簽噪聲、容量、雙下降和實驗測試誤差的直覺

撇開統計數據不談:下文推測了一些可能發生的情況，通過想象我們可以在原型網絡中得到與P. Nakkiran等人圖中所描述的相同的現象，且容量由我們所能擁有的原型數量來表示:

• 在最左邊width(參數)值1到5附近，我們的原型比類少，模型拟合程度不高（欠拟合），因為模型不能代表所有的類。

• 在width5附近，我們有10個（或者适當地更多）原形，但是，在每一個原型的訓練中損壞标簽都被擠出了，所以這些損壞标簽沒有發揮作用。

• 在width5到10這個範圍，原型收集損壞的标簽。由于每個原型都有一個用在推斷階段的“影響範圍”，所以存在一個相當大的空間，在這個空間中損壞原型與測試是非常相關的。

• 在width10以外的範圍，我們增加了更多的原形。原型之間變得更近，在推斷階段中損壞的标簽原型也被“擠出”，因此它們的“影響範圍”就會變得更小(因為比起擁有3個損壞原形，同一個類擁有5個非損壞原型中的3個的概率更大)。

這對偏差-方差分解意味着什麼? 回想一下，分解在空間上是逐點的，并像之前一樣要對各種訓練數據集進行方差和偏差處理。假設你隻有兩個類，那麼預測和标簽要麼是0要麼是1。接下來原型收集已損壞的标簽，就會産生偏差（因為你将以某種概率預測錯誤的事情)和方差（因為糟糕預測的區域取決于哪些标簽已損壞，也就是取決于我們在哪個數據集D上繪制)，并使錯誤預測的區域更小，從而減少方差和偏差。

在這種直覺中，早期停止的作用是檢測模型何時開始收集已損壞的标簽。

所以看起來現代神經網絡本質上是非參數的，其工作方式依賴于各種正則化。為了使用M. Belkin等人的公式，我們希望更加了解，我們對于各種技術如何對某些函數空間範數作用的理解到了什麼程度。似乎很難得出“傳統”統計數據表明現代學習不起作用的結論。

Hastie等人的《高維無脊最小二乘插值中的驚喜》(Surprises in High-Dimensional Ridgeless Least Squares Interpolation)一文将最小二乘作為模型問題，提供了非常全面的分析，這也可能為深度學習現象提供直覺。

在插值條件中擠出錯誤标記的數據

我們可以做一個非常簡單的插值條件的模拟。我們來思考一個由2d标準單位法線提取并沿着水平軸移動±2的點的二分類問題，并從每個類别的分配中抽取25%的點。

為了得到一個插值條件，我們使用一個具有明顯峰值的核。為了有一個易分析處理的質量并将其标準化為1，我們使用核

這個核有單位質量，在x=0時趨于無窮，且從原點衰減：

這意味着，如果我們将每一類的密度表示為樣本

處核的均值，即：

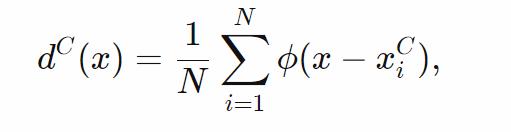
假設不同類别的點不重合(幾乎肯定如此)，我們可以根據

更大的點對每個點進行分類，或者說，如果我們想通過标準化每個點的概率密度來獲取概率

這給了我們一個插值解——在每個訓練點，标簽類有無限密度，所以它被歸類為屬于這個類。

那麼标簽錯誤發生了什麼呢? 标簽錯誤會導緻損壞的訓練點附近的某些區域被分配給錯誤的類。然而，附近正确類的點越多，錯誤分類的區域就越小。我們可以交互地嘗試。随着點數的增加，測試誤差會減少。

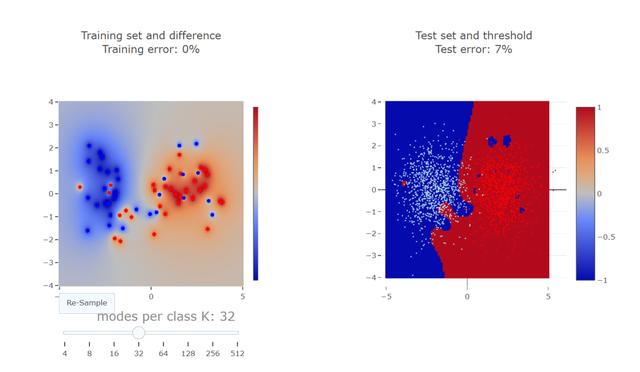
這意味着什麼呢? 這說明對于插值解，在測試時間内，良好的訓練點會擠出标記糟糕的點。

對抗示例

但是，随着數據的增加，當壞分類的區域和被随機抽樣的數據點擊中的概率減小時，随機抽樣點到下一個壞樣本的距離也減小了。這意味着除了利用模型的不良連續性(即輸入的小變化會導緻提取的特征發生大的變化)，插值條件也能使對抗例子更容易産生，因為我們隻需要特征的小變化。

特征噪聲類似于标簽噪聲

但是，雙重下降不是也發生在沒有損壞标簽的情況下嗎? 我們“僅僅”需要格外小心地處理我們的訓練數據嗎?

好吧，沒這麼簡單。高維特征在本質上可能比低維特征噪聲更多：想象一下在高維空間(比如d)中有一個兩類線性分類。我們有了有向量

和偏差

的分類器。給定輸入

，當x⋅v b≥0時，類為1;否則，類為0。如果我們預先知道輸入是有界的，我們可以找到類原型

，并使用距離

進行分類。但随後的線性分類器的d−1維零空間(null-space)中的向量，比如我們可以添加到輸入中而不改變結果的向量空間

，可能對這個距離有很大幫助，從而使得

成為對更相關的投影距離

的一個噪聲估計。

如果我們想保持在二維空間，我們可以放大噪聲維度。這就将我們引入第二個實驗。我們來繪制獨立的随機二維點，其在“特征維度”中的标準偏差為0.5，在“噪聲維度”中的标準偏差為5。這兩個類用±1分開。我們使用EM算法來将每個維度的标準偏差為1的K高斯函數的混合值拟合到每個類中。通過比較兩個拟合密度進行分類。我們使用5000個訓練點和1000個測試點。

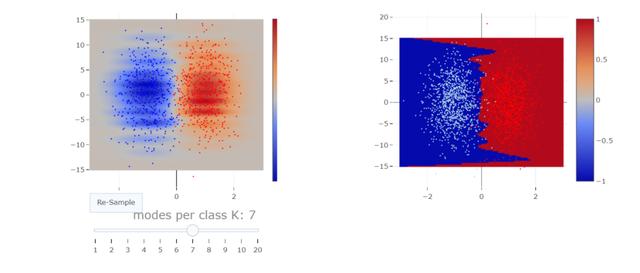
如果我們以不同的K值運行200次，并記錄其準确性，我們可以看到雙重下降中的凹凸:

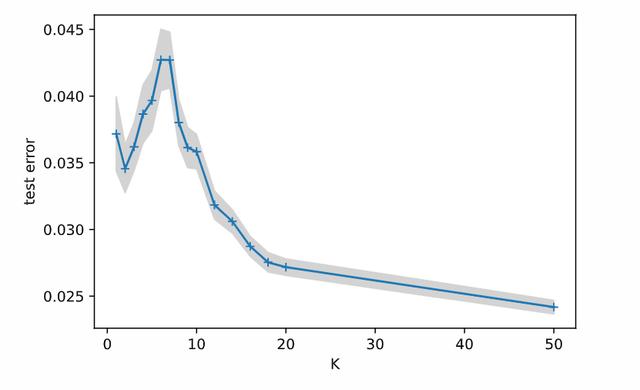
關于這些實驗的一個問題是:誤差分布是傾斜的:我們得到的很多測試誤差在2-3左右出現，可誤差在10左右還出現了一個尾巴。這條差拟合的曲線尾部的質量随分量K的數量而變化，似乎是造成中間K的平均誤差出現凹凸的主要原因。

7

結論

綜上，我們學到了什麼呢？

• 在我看來，噪音需要在推斷階段而不是在訓練階段擠出特征，由此我們看出深度學習模型的本質是非參數的。這與KDE實驗非常接近。

• 即使我們有很好的标簽(你有的，對吧？)，深度學習中的高特征維度會導緻特征中的噪音，而這些噪音的行為與标簽中的噪音類似。

原文鍊接：

https://lernapparat.de/statistics-deep-learning-nonparametric

雷峰網

更多精彩资讯请关注tft每日頭條，我们将持续为您更新最新资讯!