1.定義在R上的函數f(X)，如果滿足f(2a一X) f(X)=0，f(2b一X) f(X)=0(a≠b)，那麼f(Ⅹ)的一個周期為T=2la一b丨;

2.若函數f(x)的圖象同時關于點A(a，c)和點B(b，C)(a≠b)成中心對稱，則f(X)的一個周期為T=2丨a一b|;

3.若函數f(x)的圖像關于點A(a，c)成中心對稱又關于直線X=b成軸對稱(a≠b)，則f(X)的一個周期為T=4|a一b|。

題型一：從兩個對稱中心中挖掘出隐含的周期性。

例：奇函數f(X)的圖像關于點(1，0)對稱。且f(3)=2，則f(1)=()

[思路探尋]：圖象有兩個對稱中心，隐含函數的周期性。

奇函數〈=〉f(一X)=一f(Ⅹ)，

關于(1，0)對稱〈=〉f(2 Ⅹ) f(一X)=0

所以f(Ⅹ 2)=f(Ⅹ)，故f(1)=f(3)=2

秒殺(特值法)：因為f(x)的圖像關于點(1，0)對稱，所以f(3) f(一1)=0，因為f(x)為奇函數，所以f(一1)=一f(1)，所以f(1)=f(3)=2。

[同步跟綜]：

定義在R上的函數f(x)滿足

則(2019)的值為()。

題型二、由兩條對稱軸挖掘出隐含條件周期性。

例：設函數f(x)是定義在R上的偶函數，且f(X 2)=f(2一X)，當X∈[一2，0]時，f(X)=(√2/2)^x一1。若在區間(一2，6)内，函數g(X)=f(X)一I0ga(X 2)(a>0，且a≠1)有且隻有4個不同的零點，則實數a的取值範圍是()

[思路探尋]：

因為f(X 2)=f(2一X)。所以f(x)的圖像關于直線X=2對稱。因為f(X)是偶函數，所以圖象關于y軸對稱，f(一X)=f(X)，f(X)=f(4一X)，所以f(4一X)=f(一X)即f(X 4)=f(Ⅹ)。挖掘出隐含條件周期性。

在區間(一2，6)内，函數g(X)=f(X)一|0ga(X 2)(a>0且a≠1)有且隻有4個不同的零點。等價轉化為關于x的方程f(X)=|oga(x 2)(a>0且a≠1)。有且隻有4個不同的根。等價轉化為f(x)的圖像與h(X)=|0ga(X 2)圖像交點的個數是4。畫出兩個函數的圖象。

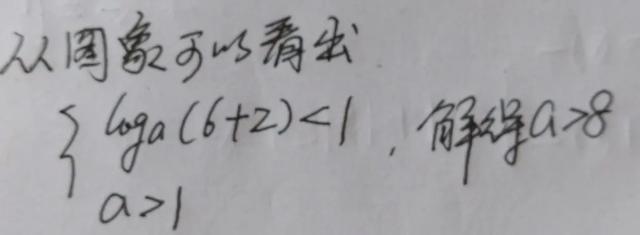
[同步跟蹤]已知函數f(x)是定義在R上的偶函數。且對任意的x∈R，f(X 2)=f(×)，當0≤Ⅹ≤1時，f(X)=Ⅹ²，若直線y=X a與函數f(X)的圖象在[0，2]内恰有兩個不同的公共點，則實數a的值是()。

題型三：一個對稱中心一條對稱軸挖掘隐含周期性

例：已知f(X)是定義在R上的偶函數，g(Ⅹ)是R上的奇函數。又知①f(3)=a(a是常數)，②g(X)=f(X一1)，試求f(2019)。

[思路探尋]：

f(X)是偶函數〈=〉f(一Ⅹ)=f(X)，

g(X)是奇函數〈=〉f(一X一1)=一f(Ⅹ一1)

=〉f(X 4)=f(X)，

f(2019)=f(504x4 3)=f(3)=a。

[同步跟蹤]：

已知f(x)是定義域為(一∞， ∞)的奇函數，滿足f(1一X)=f(1 X)。若f(1)=2，則f(1) f(2) f(3) …f(50)=()

參考答案：2

我是數學山人行，歡迎關注！！！點評感謝！！！

更多精彩资讯请关注tft每日頭條，我们将持续为您更新最新资讯!