二次函數作為初中數學的核心内容，也是重要的基礎知識和重要的數學思想方法，其自身結構特點和它在數學中的地位決定了：二次函數不僅與數學其他知識有着密切的聯系，中将二次函數知識與我們的學習生活、經濟發展、生産勞動等實際問題相結合的題型，在全國各地中考數學卷中更是倍受青睐。

因此，二次函數可以說是聯系數學知識間或數學與實際問題間的紐帶和橋梁，本文将着重分析的二次函數實際應用問題則是中考數學中不可或缺的重要内容。

按照常考的實際問題種類，可将二次函數的實際應用分為：利潤（營業額）最大問題、面積最大問題和實際抛物線問題。

下面，本文将通過經典真題重現的方式，對這三類問題進行試題分析，最後歸納與總結出解決這些問題的一般方法。

1、 利潤最大問題

例1．（2019秋•武邑縣校級期末）某校九年級學生小麗、小強和小紅到某超市參加了社會實踐活動，在活動中他們參與了某種水果的銷售工作．已知該水果的進價為每千克8元，下面是他們在活動結束後的對話．

小麗；如果以每千克10元的價格銷售，那麼每天可售出300千克．

小強：如果每千克的利潤為3元，那麼每天可售出250千克．

小紅：如果以每千克13元的價格銷售，那麼每天可獲取利潤750元．

（1）已知該水果每天的銷售量y（千克）與銷售單價x（元）之間存在一次的函數關系，請根據他們的對話，判決該水果每天的銷售量y（千克）與銷售單價x（元）之間存在怎樣的函數關系，并求出這個函數關系式；

（2）設該超市銷售這種水果每天獲取的利潤為W（元），求W（元）與x（元）之間的函數關系式．當銷售單價為何值時，每天可獲得的利潤最大？最大利潤是多少元？

（3）當銷售利潤為600元并且盡量減少庫存時，銷售單價為每千克多少元？

【分析】（1）依據題意首先确定學生對話中一次函數關系；

（2）根據銷售利潤＝銷售量×（售價﹣進價），列出平均每天的銷售利潤w（元）與銷售價x之間的函數關系；

（3）依據函數的增減性求得最大利潤．

【解答】：（1）當銷售單價為13元/千克時，銷售量為：750÷（13﹣8）＝150千克，設y與x的函數關系式為：y＝kx b（k≠0）

把（10，300），（13，150）分别代入得：k＝﹣50，b＝800，

∴y與x的函數關系式為：y＝﹣50x 800（x＞0）．

（2）∵利潤＝銷售量×（銷售單價﹣進價），

根據題意得：

W＝（﹣50x 800）（x﹣8）

＝﹣50（x﹣12）² 800，

∴當銷售單價為12元時，每天可獲得的利潤最大，最大利潤是800元．

（3）将w＝600代入二次函數W＝（﹣50x 800）（x﹣8）＝600，

解得：x₁＝10，x₂＝14（舍去），

即：當銷售利潤為600元并且減少庫存時，銷售單價為每千克10元．

【方法點評】本題考查了二次函數的性質在實際生活中的應用．最大銷售利潤的問題常利函數的增減性來解答，我們首先要吃透題意，确定變量，建立函數模型，然後結合實際選擇最優方案．

這是一道與二次函數有關的實際應用問題，貼近生活，考生能學習生活知識，同時更幫助學生理解數學知識和生活之間的關系。研究題目，吃透題型是數學學習最有效，最實際的學習探究行為。從題目中挖掘知識點和方法技巧，提煉解題方法，概括題型，這樣數學學習才能越學越有效，越學越輕松。

現代數學教育要求學生能體會數學與現實生活的緊密聯系，增強應用意識，提高運用數學知識和方法技巧解決問題的能力。在近幾年的中考數學試題中，經常出現與二次函數有關的實際應用問題，此類題型，有時候因其條件多，題目長，很多同學無從下手,難以快速找到解題思路。

變式1．（2019秋•餘姚市期末）小穎家經營着一家水果店，在楊梅旺銷季節，她的父母經常去果園采購楊梅用于銷售．果園的楊梅價格如下：購買數量不超過20筐，每筐進價20元；購買數量超過20筐，每筐進價18元．小穎在觀察水果店一段時間的銷售情況後發現，當楊梅的售價為每筐30元時，每天可銷售30筐；每筐售價提高1元，每天銷量減少1筐；每筐售價降低1元，每天銷量增加1筐．若每天購進的楊梅能全部售出，且售價不低于進價，從果園進貨的運費為每天100元．

（1）設售價為每筐x元，則每天可售出　 　筐．

（2）當每筐楊梅的售價定為多少元時，楊梅的日銷售利潤最大？最大日利潤是多少元？

【解答】：（1）根據題意得：每天可售出30﹣（x﹣30）＝60﹣x[或30 （30﹣x）＝60﹣x]，故答案為：（60﹣x）．

（2）設每筐楊梅的售價為x元，每天的楊梅銷售利潤為y，

①當60﹣x≤20，即x≥40時，y＝（x﹣20）（60﹣x）﹣100＝﹣x² 80x﹣1300＝﹣（x﹣40）² 300

此時售價為40元，最大利潤為300元；

②當60﹣x＞20，即x＜40時y＝（x﹣18）（60﹣x）﹣100＝﹣x² 78x﹣1060＝﹣（x﹣39）² 341

此時售價為39元，最大利潤為341元；

∵341＞300，∴當每筐楊梅的售價定為39元時，

每天的楊梅銷售利潤最大，最大利潤為341元．

變式2. （2019秋•東台市期末）某網店打出促銷廣告：最潮新款服裝30件，每件售價300元，若一次性購買不超過10件時，售價不變；若一次性購買超過10件時，每多買2件，所買的每件服裝的售價均降低6元．已知該服裝成本是每件200元．設顧客一次性購買服裝x件時，該網店從中獲利y元．

（1）求y與x的函數關系式，并寫出自變量x的取值範圍．

（2）顧客一次性購買多少件時，該網店從中獲利最多，并求出獲利的最大值？

【解答】：（1）y＝100x（（0≤x≤10的整數）；y＝﹣3x² 130x（10⟨x≤30的整數）；

（2）當0≤x≤10的整數y＝100x，當10時，利潤有最大值y＝1000元；

當10˂x≤30時，y＝﹣3x2 130x，

當x＝-b/2a=65/3時，y取最大值，

因為x為整數，根據對稱性得：當x＝22時，y有最大值＝1408元˃1000元，

所以顧客一次性購買22件時，該網站獲利最多．

變式3. （2019秋•高郵市期末）5G網絡比4G網絡的傳輸速度快10倍以上，因此人們對5G産品充滿期待．華為集團計劃2020年元月開始銷售一款5G産品．根據市場營銷部的規劃，該産品的銷售價格将随銷售月份的變化而變化．若該産品第x個月（x為正整數）銷售價格為y元/台，y與x滿足如圖所示的一次函數關系：且第x個月的銷售數量p（萬台）與x的關系為p＝x 1．

（1）該産品第6個月每台銷售價格為_______元；

（2）求該産品第幾個月的銷售額最大？該月的銷售價格是多少元/台？

（3）若華為董事會要求銷售該産品的月銷售額不低于27500萬元，則預計銷售部符合銷售要求的是哪幾個月？

（4）若每銷售1萬台該産品需要在銷售額中扣除m元推廣費用，當6≤x≤8時銷售利潤最大值為22500萬元時，求m的值．

【解答】：（1）設y與x滿足如圖所示的一次函數關系為y＝kx b，

将（2，6500）、（4，5500）代入，得

k＝﹣500，b＝7500，

所以y＝﹣500x 7500．

當x＝6時，y＝4500．

答：該産品第6個月每台銷售價格為4500元；

故答案為4500；

（2）設該産品月銷售額為w元，根據題意，得

w＝py＝（x 1）（﹣500x 7500）

＝﹣500（x﹣7）² 32000

當x＝7時，即該産品第7個月的銷售額最大，

該月的銷售價格是﹣500×7 7500＝4000元/台；

答：該産品第7個月的銷售額最大，該月的銷售價格是4000元/台；

（3）根據題意，得

﹣500（x﹣7）² 32000＝27500

解得x₁＝4，x₂＝10，

根據抛物線可知：

﹣500＜0，抛物線開口向下，

銷售該産品的月銷售額不低于27500萬元，

則預計銷售部符合銷售要求的是4、5、6、7、8、9、10月；

（4）根據題意，得當6≤x≤8時，共銷售24萬台，

扣除24m萬元推廣費用，

∴w＝（x 1）（﹣500x 7500）﹣24m

＝﹣500（x﹣7）² 32000﹣24m

32000﹣24m＝22500

解得m＝2375/6．

答：m的值為2375/6萬元．

變式4．（2020•松滋市一模）金松科技生态農業養殖有限公司種植和銷售一種綠色羊肚菌，已知該羊肚菌的成本是12元/千克，規定銷售價格不低于成本，又不高于成本的兩倍．經過市場調查發現，某天該羊肚菌的銷售量y（千克）與銷售價格x（元/千克）的函數關系如下圖所示：

（1）求y與x之間的函數解析式；

（2）求這一天銷售羊肚菌獲得的利潤W的最大值；

（3）若該公司按每銷售一千克提取1元用于捐資助學，且保證每天的銷售利潤不低于3600元，問該羊肚菌銷售價格該如何确定．

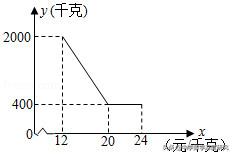
【解答】：（1）①當12≤x≤20時，設y＝kx b．代（12，2000），（20，400），

解得k=-200,b=4400,∴y＝﹣200x 4400.

②當20＜x≤24時，y＝400．

（2）①當12≤x≤20時，

W＝（x﹣12）y

＝（x﹣12）（﹣200x 4400）

＝﹣200（x﹣17）² 5000

當x＝17時，W的最大值為5000；

②當20＜x≤24時，

W＝（x﹣12）y＝400x﹣4800．

當x＝24時，W的最大值為4800．

∴最大利潤為5000元．

（3）①當12≤x≤20時，

W＝（x﹣12﹣1）y

＝（x﹣13）（﹣2000x 4400）

＝﹣200（x﹣17.5）² 4050.

令﹣200（x﹣17.5）² 4050＝3600

x₁＝16，x₂＝19，∴定價為16≤x≤19.

②當20＜x≤24時，

W＝400（x﹣13）＝400x﹣5200≥3600,

∴22≤x≤24．

綜上，銷售價格确定為16≤x≤19或22≤x≤24．

二、面積最大問題

例2．（2019秋•寶安區期末）光明農場準備修建一個矩形苗圃園，苗圃一邊靠牆，其他三邊用長為48米的籬笆圍成．已知牆長為a米．設苗圃園垂直于牆的一邊長為x米．

（1）求當x為多少米時，苗圃園面積為280平方米；

（2）若a＝22米，當x取何值時，苗圃園的面積最大，并求最大面積．

【分析】（1）根據題意得方程求解即可；

（2）設苗圃園的面積為y，根據題意得到二次函數解析式y＝x（48﹣2x）＝﹣2x² 48x，根據二次函數的性質求解即可．

【解答】（1）：根據題意得：（48﹣2x）x＝280，

解得：x＝10或x＝14，

∴當x為10米或14米時，苗圃園面積為280平方米；

（2）：設苗圃園的面積為y平方米，則y＝x（48﹣2x）＝﹣2x² 48x＝﹣2（x﹣12）² 288

∵二次項系數為負，∴苗圃園的面積y有最大值．

∴當x＝12時，即平行于牆的一邊長是24米，24＞22，不符題意舍去；

∴當x＝13時，y最大＝286平方米；

答：當x＝13米時，這個苗圃園的面積最大，最大值為286平方米．

【方法點評】本題考查了二次函數、一元二次方程、一元二次不等式的實際應用問題．解題的關鍵是根據題意構建二次函數模型，然後根據二次函數的性質求解即可．

變式1．（2019秋•瑞安市期末）如圖，一面利用牆，用籬笆圍成的矩形花圃ABCD的面積為Sm²，垂直于牆的AB邊長為xm．

（1）若牆可利用的最大長度為8m，籬笆長為18m，花圃中間用一道籬笆隔成兩個小矩形．

①求S與x之間的函數關系式；

②如何圍矩形花圃ABCD的面積會最大，并求最大面積．

（2）若牆可利用最大長度為50m，籬笆長99m，中間用n道籬笆隔成（n 1）小矩形，當這些小矩形都是正方形且x為正整數時，請直接寫出所有滿足條件的x、n的值．

【解答】：（1）①由題意得：

S＝x×（18﹣3x）＝﹣3x² 18x（10/3≤x＜6）；

②由S＝﹣3x² 18x＝﹣3（x﹣3）² 27，

∴當x＝10/3米時，S最大，為80/3平方米；

（2）根據題意可得：（n 2）x （n 1）x＝99，

則n＝3，x＝11；或n＝4，x＝9，或n＝15，x＝3，或n＝48，x＝1．

變式2．（2019秋•雨花台區期末）某養殖場計劃用96米的竹籬笆圍成如圖所示的①、②、③三個養殖區域，其中區域①是正方形，區域②和③是矩形，且AG：BG＝3：2．設BG的長為2x米．

（1）用含x的代數式表示DF＝_______；

（2）x為何值時，區域③的面積為180平方米；

（3）x為何值時，區域③的面積最大？最大面積是多少？

【解答】：（1）∵區域①是正方形，區域②和③是矩形，

AG：BG＝3：2．設BG的長為2x米，則AG＝3x，

∴AP＝GH＝BE＝PH＝AG＝3x，EH＝GB＝2x，

DC＝PE＝AB＝5x，

∴DF＝1/2（96﹣3×5x﹣3×3x）＝48﹣12x．

故答案為48﹣12x．

（2）根據題意，得5x（48﹣12x）＝180，

解得x1＝1，x2＝3

答：x為1或3時，區域③的面積為180平方米；

（3）設區域③的面積為S，

則S＝5x（48﹣12x）

＝﹣60x² 240x

＝﹣60（x﹣2）² 240.

∵﹣60＜0，∴當x＝2時，S有最大值，最大值為240.

答：x為2時，區域③的面積最大，為240平方米．

變式3（2019秋•鎮江期末）某興趣小組想借助如圖所示的直角牆角ADC（兩邊足夠長），用20m長的籬笆圍成一個矩形ABCD花園（籬笆隻圍AB、BC兩邊）．

（1）若圍成的花園面積為91m²，求花園的邊長；

（2）在點P處有一顆樹與牆CD，AD的距離分别為12m和6m，要能将這棵樹圍在花園内（含邊界，不考慮樹的粗細），又使得花園面積有最大值，求此時花園的邊長．

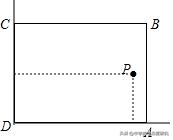
【解答】：（1）設AB長為xm．由題意得：x（20﹣x）＝91；

解得：x₁＝13，x₂＝7；

當x＝13時，BC＝20﹣13＝7；

當x＝7時，BC＝20﹣7＝13；

答：花園的邊長為：13m和7m．

（2）設花園的一邊長為x，面積為y．y＝x（20﹣x）＝﹣x² 20x＝﹣（x﹣10）² 100，

解得：6≤x≤8，或12≤x≤14．

當x＝8或12時，y有最大值為96，此時花園的邊長為8cm或12cm．

三、實際抛物線問題

例3．（2019秋•漢陽區校級月考）有一個直徑為16米的圓形噴水池，噴水池的周邊有一圈噴水頭，噴出的水柱為抛物線，在距水池中心3米處達到最高，高度為5米，且各方向噴出的水柱恰好在噴水池中心的立杆上點T處彙合．如圖所示為截面圖，以水平方向為x軸，噴水池中心為原點建立直角坐标系．

（1）求水柱所在抛物線（第一象限部分）的函數解析式；

（2）正在噴水時，身高1.8米的人，應站在離水池中心多遠的地方就能不被淋濕？

（3）在噴出水柱的形狀不變的前提下，把水池的直徑擴大到32米，各方向噴出的水柱仍在噴水池中心的立杆上點T處彙合，請探究擴建後噴水池水柱的最大高度．

【分析】（1）根據頂點坐标可設二次函數的頂點式，代入點（8，0），求出a值，此題得解；（2）利用二次函數圖象上點的坐标特征，求出當y＝1.8時x的值，由此即可得出結論；

（3）利用二次函數圖象上點的坐标特征可求出抛物線與y軸的交點坐标，由抛物線的形狀不變可設改造後水柱所在抛物線（第一象限部分）的函數表達式為y＝﹣1/5x2 bx 16/5，代入點（16，0）可求出b值，再利用配方法将二次函數表達式變形為頂點式，即可得出結論．

【解答】：（1）設水柱所在抛物線（第一象限部分）的函數表達式為y＝a（x﹣3）² 5（a≠0），

将（8，0）代入y＝a（x﹣3）² 5，得：25a 5＝0，解得：a＝﹣1/5，

∴水柱所在抛物線（第一象限部分）的函數表達式為y＝﹣1/5（x﹣3）² 5（0＜x＜8）．

（2）當y＝1.8時，有﹣1/5（x﹣3）² 5＝1.8，

解得：x₁＝﹣1，x₂＝7，

∴為了不被淋濕，身高1.8米的人，站立時必須在離水池中心7米以内；

（3）當x＝0時，y＝﹣1/5（x﹣3）² 5＝16/5．

設改造後水柱所在抛物線（第一象限部分）的函數表達式為y＝﹣1/5x² bx 16/5，

∵該函數圖象過點（16，0），

∴0＝﹣1/5×16² 16b 16/5，解得：b＝3，

∴改造後水柱所在抛物線（第一象限部分）的函數表達式為y＝﹣1/5x² 3x 16/5＝﹣1/5（x﹣15/2）² 289/20．

∴擴建改造後噴水池水柱的最大高度為289/20米．

【方法點評】本題考查了待定系數法求二次函數解析式以及二次函數圖象上點的坐标特征，解題的關鍵是：（1）根據點的坐标，利用待定系數法求出二次函數表達式；（2）利用二次函數圖象上點的坐标特征求出當y＝1.8時x的值；（3）根據點的坐标，利用待定系數法求出二次函數表達式．

變式1．（2019秋•西城區期末）圖1是一個傾斜角為α的斜坡的橫截面，tanα＝1/2．斜坡頂端B與地面的距離BC為3米．為了對這個斜坡上的綠地進行噴灌，在斜坡底端安裝了一個噴頭A，噴頭A噴出的水珠在空中走過的曲線可以看作抛物線的一部分．設噴出水珠的豎直高度為y（單位：米）（水珠的豎直高度是指水珠與地面的距離），水珠與噴頭A的水平距離為x（單位：米），y與x之間近似滿足函數關系y＝ax² bx（a，b是常數，a≠0），圖2記錄了x與y的相關數據

（1）求y關于x的函數關系式；

（2）斜坡上有一棵高1.8米的樹，它與噴頭A的水平距離為2米，通過計算判斷從A噴出的水珠能否越過這棵樹．

【解答】（1）：在Rt△ABC中，tanα＝1/2，BC＝3，∴AC＝6．

∴點B的坐标為（6，3）．

所以水珠能越過這棵樹．

變式2. （2018秋•無為縣期末）如圖，三孔橋橫截面的三個孔都呈抛物線形，兩個小孔形狀、大小都相同，正常水位時，大孔水面常度AB＝20米，頂點M距水面6米（即MO＝6米），小孔水面寬度BC＝6米，頂點N距水面4.5米．航管部門設定警戒水位為正常水位上方2米處借助于圖中的平面直角坐标系解答下列問題：

（1）在汛期期間的某天，水位正好達到警戒水位，有一艘頂部高出水面3米，頂部寬4米的巡邏船要路過此處，請問該巡邏船能否安全通過大孔？并說明理由．

（2）在問題（1）中，同時橋對面又有一艘小船準備從小孔迎面通過，小船的船頂高出水面1.5米，頂部寬3米，請問小船能否安全通過小孔？并說明理由．

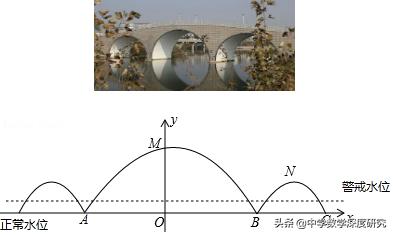
【解答】：（1）設大孔所在的抛物線的解析式為y＝ax2 6，

由題意得，A（﹣10，0），

∴a（﹣10）² 6＝0，∴a＝﹣3/50，

∴大孔所在的抛物線的解析式為y＝﹣3/50x² 6，

當x＝2時，y＝﹣3/50×2² 6＝5.76＞5，

∴該巡邏船能安全通過大孔；

（2）建立如圖所示的平面直角坐标系，

設小孔所在的抛物線的解析式為z＝mx² 4.5，

由題意得，C（3，0），

∴m×3² 4.5＝0，∴m＝﹣1/2，

∴小孔所在的抛物線的解析式為z＝﹣1/2x² 4.5，

當x＝1.5時，z＝3.375＜3.5，

∴小船不能安全通過小孔．

從以上3個不同類型的二次函數實際應用問題，我們不難發現，這類問題最終都能轉化成求二次函數的最值問題。

我們還能總結出解決此類問題的一般方法：

①先求出實際問題中對應的二次函數的表達式（利潤（營業額）最大問題和面積最大問題一般可以根據題意直接表示出二次函數的表達式，實際抛物線問題需要建立适當的直角坐标系再用待定系數法求解），需注意的是：若求出的二次函數表達式不是頂點式，需配方成頂點式；

②根據題意求出實際問題中自變量的取值範圍；

③根據二次函數的圖象和性質，結合②中求出的自變量的取值範圍，最終解決問題。

在掌握了解題的基本步驟後，在解決實際問題時，還有2點尤其需要注意：

①善于将實際問題轉化為數學問題，再轉化為函數問題；

②注意自變量的取值範圍，不僅保證函數解析式有意義，還要保證符合實際意義。

二次函數在我們的日常生活中應用廣泛，《新課标改革》也強調要讓學生感受到數學知識來源于生活，同時又服務于生活，充分認識到數學知識與現實生活中的實際問題聯系緊密。

應用二次函數解決實際問題，對學生的邏輯思維等能力要求較高，加上一些學生知識面過窄，缺乏生活經驗，對所學知識不能靈活應用等原因，總是拿不到高分。

因此，考生要想提高此類問題的解決能力，就必須要細心觀察生活，增強應用意識，會分析一些現實生活中的實際問題與數學之間的關系，提高運用數學知識、建立模型等方法解決問題的能力。

更多精彩资讯请关注tft每日頭條，我们将持续为您更新最新资讯!