高中數學中線面角射影怎麼找-tft每日頭條

高中數學中線面角射影怎麼找

教育更新时间:2024-05-07 08:21:49

立體幾何中求二面角是曆年高考常考熱點之一。求二面角的方法很多，常用的有定義法、三垂線法、法向量法等。不過本節課我們主要學習利用射影面積法求二面角。

射影面積求二面角的方法适用于不易作出二面角的平面角時。

平面ABC與平面a所成二面角為θ，它在平面a内的投影為DBC，則平面ABC與平面a所成二面角的餘弦值為射影面積與原面積的比：

高中數學中線面角射影怎麼找（射影面積法求二面角的推導及其應用）1

高中數學中線面角射影怎麼找（射影面積法求二面角的推導及其應用）2

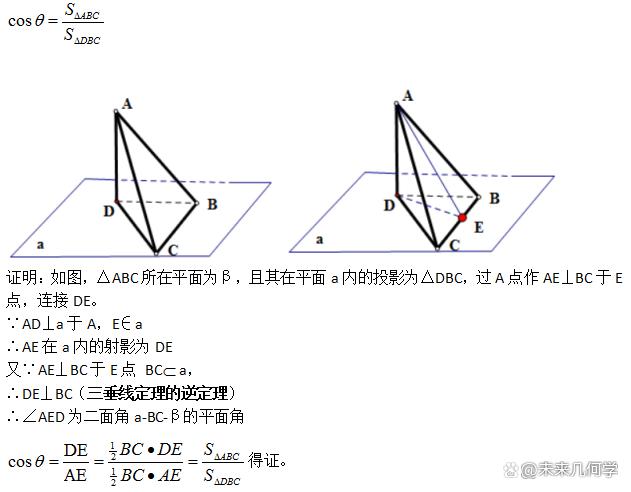
數學學習

下面我們再用兩道例題來詳細說明利用射影面積法求二面角的方法：

例1、四棱錐S-ABCD的底面是正方形，SD⊥平面ABCD，SD=AD=a，點E是SD上的點，且DE=λa（0<λ<1）,AC⊥BE。若二面角C-AE-D的大小為600，求λ的值。

高中數學中線面角射影怎麼找（射影面積法求二面角的推導及其應用）3

高中數學中線面角射影怎麼找（射影面積法求二面角的推導及其應用）4

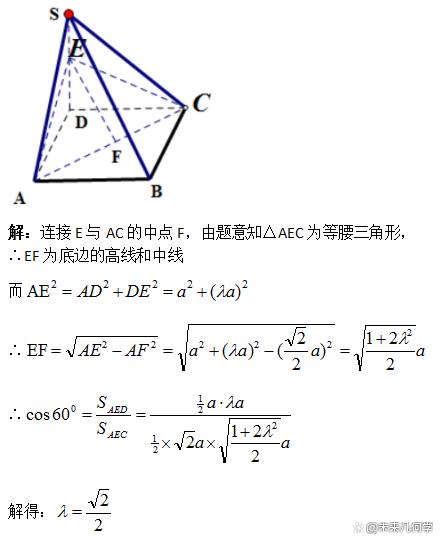
好了，今天的内容就分享到這裡，如果您有疑問，可以在文章下方留言，歡迎繼續關注，精彩還将繼續！

更多精彩资讯请关注tft每日頭條，我们将持续为您更新最新资讯!

查看全部

网友关注

教育父親的病主要内容
1、《父親的病》主要内容：作者兒時的紹興城，父親患了嚴重的水腫病，長年無法康複，家裡請了兩位人稱“神... 2023-07-06
教育英語勵志短文
ThePoweroftheDreamWhensomeonelooksintoyoureyesthey... 2023-07-06
教育流水步距和流水工期怎麼計算
1、流水步距的計算方法：流水步距=最大公約數｛流水節拍｝，意思是保證該分部工程完成，相鄰兩個分項工程... 2023-07-06
教育驚弓之鳥的意思和寓意
1、驚弓之鳥：被弓箭吓怕了的鳥不容易安定。原指以巧制勝，現以“驚弓之鳥”來形容受過驚吓的人碰到一點動... 2023-07-06
教育歡聲笑語類似的詞語
1、歡聲笑語類似的成語：興高采烈。2、歡聲笑語（讀作：huānshēngxiàoyǔ），是中國漢語詞... 2023-07-06
教育略無慕豔意略的意思
1、略無慕豔意的略釋義：絲毫。“略無慕豔意”是絲毫都沒有羨慕的想法。出自《送東陽馬生序》。2、《送東... 2023-07-06
教育漢字手抄報簡單又漂亮文字内容
1、漢字，屬于表意文詞素音節文字。漢漢語寫用文字，也被借用于書寫日韓語、越南語等語言，是漢字文化圈廣... 2023-07-06
教育郁達夫的代表作
1、郁達夫的代表作主要作品有：《沉淪》、《茑蘿集》、《小說論》，《日記九種》、《空虛》、《迷羊》、《... 2023-07-06
教育祖國在我心中手抄報内容簡短
1、祖國，一個多麼輝煌的名字，他是我們全中國人民火熱的心。每個人都希望祖國能夠建設好，能過上好日子。... 2023-07-06
教育夕字五筆怎麼打
1、夕五筆：QTNY。2、夕是成字根，就在Q鍵上，按照成字根的打法來，先報戶口，再按筆畫順序來。3、... 2023-07-06
教育改革開放的意義和影響有哪些
改革開放是決定當代中國命運的關鍵抉擇，是發展中國特色社會主義，實現中華民族偉大複興的必經之路。近40... 2023-07-06
教育嶄新的反義詞是什麼
1、嶄新的反義詞：陳舊、古舊、陳腐、破舊；2、嶄新，讀音為zhǎnxīn，漢語詞語，意思是非常新、簇... 2023-07-06
教育學習收獲怎麼寫
1、要确定培訓内容，這樣才好為心得體會寫大綱。2、明确每一天培訓的具體課程，這樣可以讓我們更好的入手... 2023-07-06
教育孩子一年級考試成績不好怎麼辦
1、即使千叮咛萬囑咐的讓老師嚴厲管教孩子，不聽話可以打，可以罵，依然沒有老師敢打敢罵，這樣的情況下，... 2023-07-06
教育茉莉花的介紹和特點
茉莉花是木犀科、素馨屬直立或攀援灌木，高達3米。小枝圓柱形或稍壓扁狀，有時中空，疏被柔毛。葉對生，單葉，葉片紙質，圓形、橢圓形、卵狀橢圓形或倒卵形，兩端圓或鈍，基部有時微心形，在上面稍凹入或凹起，下面凸起，細脈在兩面常明顯，微凸起，除下面脈腋間常具簇毛外，其餘無毛。茉莉性喜溫暖濕潤，在通風良好、半陰的環境生長最好。土壤以含有大量腐殖質的微酸性砂質土壤為最适合。多數品種畏寒、畏旱，不耐霜凍、濕澇和堿 2023-07-06
教育北大會計專碩就業前景如何
前景很不錯。該專業可以從事的崗位有：1、政府及涉财公務機關。當前,各級政府的财務崗位:财政、稅務、工... 2023-07-06
教育焦急的反義詞
1、焦急反義詞：（1）耐心(注釋:不急躁﹐不厭煩。指不急躁﹑不厭煩的性格。)（2）從容(注釋:鎮定，... 2023-07-06
教育抒發豪情壯志的詩句
1、亦餘心之所善兮，雖九死其猶未悔。——屈原《離騷》2、詞源倒傾三峽水，筆陣獨掃千人軍。——杜甫《醉... 2023-07-06
教育教師資格證哪個最好考
1、幼兒教師資格證最好考，因為它的考試内容相對簡單，筆試考兩科，較之中學少備考一科學科知識，但筆試和... 2023-07-06
教育高考有哪些科目
1、高考科目有語文、數學、外語、理科綜合（物理、化學、生物）或文科綜合（思想政治、曆史、地理），我國... 2023-07-06
教育分享作文
1、快樂，來自父母無微不至的照顧;快樂，來自朋友好言相勸的關懷;快樂，來自對手一個真誠的握手;快樂，... 2023-07-06
教育在水一方詩經原文
1、蒹葭蒼蒼，白露為霜。所謂伊人，在水一方。溯洄從之，道阻且長。溯遊從之，宛在水中央。2、蒹葭萋萋，... 2023-07-06
教育田忌賽馬誰為田忌出的主意
1、田忌賽馬是孫膑為田忌出的主意，是揭示如何善用自己的長處，來對付别人的短處的一個實例。2、當時齊國... 2023-07-06
教育林清玄散文賞析
1、賞析：一株小小的野百合,演繹出一段美麗而又令人感動的故事。這就是台灣作家林清玄的散文《心田上的百... 2023-07-06
教育開證明怎麼寫
1、文頭。證明兩個字居住，加粗，加大字号。2、正文内容。輸入正文内容，需要證明的事項等。叙述簡介，明... 2023-07-06
教育常見的成語及解釋是什麼
1、人迹罕至：罕：少。人的足迹很少到達。指荒涼偏僻的地方。2、人聲鼎沸：鼎：古代煮食器；沸：沸騰。形... 2023-07-06
教育明朝怎麼被清朝滅了
1、明朝并不是被清朝滅亡的，而是被李自成的農民起義軍攻克北京推翻的。明朝晚期，因東林黨争和天災外患，... 2023-07-06
教育複刻是什麼意思
1、意思是指木刻書籍的重行刻印，出自阿英《版本小言》（于1935年）：“但‘善本’也不一定是初刻，有... 2023-07-06
教育冒昧的昧是什麼意思
1、冒昧的昧的意思：輕率，魯莽。2、冒昧是一個漢語詞彙，是指不顧地位、能力、場合是否适宜(多用做謙詞... 2023-07-06
教育我家的小貓作文400字
1、“喵喵”你聽又是我奶奶家的小花貓在叫了！他呀可是我們家的“小調皮”天天在家裡叫啊！，隻要我一到奶... 2023-07-06

tft每日頭條

> 教育

> 高中數學中線面角射影怎麼找

高中數學中線面角射影怎麼找

相关教育资讯推荐

热门教育资讯推荐

网友关注