孩子初一數學成績很好，一到初二，數學成績直線下降，這是很多孩子會遇到的問題。

近日，我接到幾位家長的電話，都是反應孩子遇到了四邊形的難題，坐那思考半天還是不會做。作為一名長期從事數學教學的一線教師，有必要和大家分享一點初中數學幾何的學習方法。

幾何是數學一個分支，它對于培養學生的識圖、畫圖能力及邏輯思維能力和推理論證能力都是十分重要的，如果做做到以下幾點，你就不會再害怕幾何難題了。

學生進行初中，在初一全年所學習的幾何知識大多是基礎知識，如線段、角、三角形等有關知識，這些圖形學生在小學都已見過，學習起來覺得輕松，所以初一數學成績都還不錯。但正是因為學生感覺到簡單，往往忽略了一些要點。

幾何的基礎知識，是指定義、公理、定理（推論），特别是基本圖形的幾何語言描述、基本幾何作圖的規範語言以及一些概念性的東西。

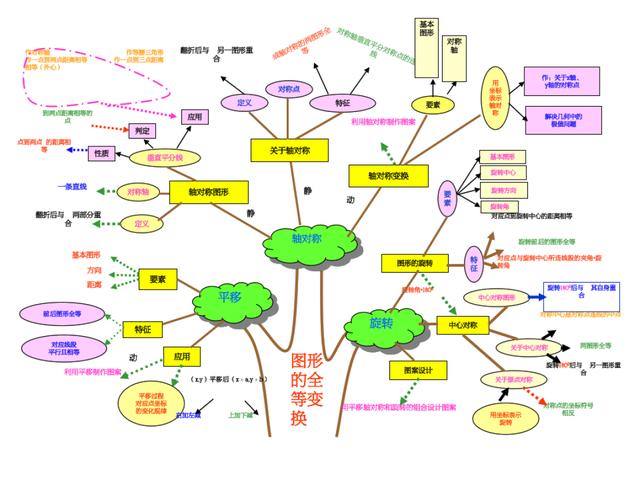
例：幾何知識樹狀圖

在實際教學中，有時我會讓學生像背誦古詩一樣去背誦一些定理、定義，背誦的過程是一個知識内化的過程，但僅僅是背誦的程度還不夠，真正内化，就是要真正理解，在解決簡單問題的過程中不斷規範運用，切不可想當然，看表面。

基本的幾何圖形，要能用規範的幾何語言表述，幾何基本作圖，要能用規範的幾何語言描述作圖過程。初中幾何除定義外，還有10條公理、140多條定理，全部理解并掌握了是學好初中幾何的基礎，隻有有了足夠的知識儲備，才能在解決幾何問題的時候得心應手。

初中幾何大多都是在接觸新圖形，從最基本的圖形"點"到時"線"再到"線的組合圖形"，按照認知規律逐漸深入，先介紹圖形，認識圖形，了解定義，再學習該圖形的性質，最後學習圖形的判定，基本都是這樣一個學習流程，圖形的定義往往既是性質又可作為判定。

這裡所說的分類，是指随着學習的深入，總結知識點的前後聯系，以知識點為主幹，其他點為枝的分類方法。

以"垂直"為例，初一學習垂直，在初二和初三的學習中，許多圖形中都用到垂直，可以總結分類。

平行線中的垂直：一條直線垂直兩條平行線中的一條，那麼一定垂直另一條。

直角三角形中的垂直：直角三角形兩銳角互餘、勾股定理、射影定理。

四邊形中的垂直：菱形對角線互相垂直平分，矩形（含正方形）四個内角都是直角。

圓中的垂直：圓中直徑所對圓周角是直角、圓的切線與過切點半（直）徑垂直。

如果在學習過程中，不斷總結這點特點和規律，到初三的時候，就很容易建立起初中平面幾何的整體框架，解決綜合性較強有大題時有了充足的知識儲備，看到圖形聯想到學過的知識點，解決起來就容易多了。

分析問題、解決問題的方法有很多種，諸如"綜合法"、"分析法"、"反證法"、"枚舉法（窮舉法）、完全歸納法、不完全歸納法……等等。

• 1.綜合法

綜合法是一種直接證法，從已知條件出發，借助其性質和有關定理，經過逐步的邏輯推理，最後達到待證結論或需求問題，其特點和思路是"由因到果"，即從"已知"看"可知"，逐步推向"未知"。

适用題型：适用于已知條件相對較少的題目。

步驟：綜合已知條件，看能夠得到什麼樣的結論，選擇與待證結論相關的再結合其他已知條件進一步論證，如此反複，最終達到待證的結論。

用綜合法解決問題時，每一個中間論都會得到若幹個結論，選擇恰當的中間結論進一步論證是綜合法的關鍵。

分析法是一種間接證法，從要證的結論出發，逐步尋求使它成立的充分條件，直到歸結為判定一個顯然成立的條件（已知條件、定義、公理、定理、性質、法則等）為止，從而證明論點的正确性、合理性的論證方法。也稱為因果分析、逆推證法或執果索因法。

适用題型：已知條件相對較多的題目，或者使用直接證法比較困難的題目。

步驟：從待證的結論出發，"要證……，隻需證明（知道）……"，排除已知條件和顯然成立的條件，重複"要證……，隻需證明（知道）……，直到所需條件全部成立，于是問題得證。

分析法是分析問題、解決問題最常用的一種方法。我們通常用分析法對問題進行分析，然後使用綜合法寫出解決問題的過程。

• 3.反證法

又稱歸謬法、背理法，是一種間接證法，首先假設某命題不成立（即在原命題的條件下，結論不成立），然後推理出明顯矛盾的結果，從而下結論說原假設不成立，原命題得證。

适用題型：唯一性命題、否定性命題、"至多"，"至少"型命題、不等量問題

步驟：先假設命題結論不成立，即假設結論的反面成立。從這個假設的命題出發，經過推理證明得出矛盾。最後由矛盾判斷假設不成立，從而肯定命題的結論正确。

當我們面對一道幾何題時，如果問題相對簡單，我們通過直接觀察就很容易找到解決的方法。但對于一些相對複雜、難度較大的題目時，大多數同學感到無從下手，甚至放棄。真的就放棄了嗎？可以按以下步驟試一試，說不定就找到了問題的突破口。

再畫一遍圖形

• 1. 再畫一遍圖形

雖然題目已經給出了明細的圖形，但我們在充分了解題意的基礎上，動手再畫一遍圖形，在畫圖的過程中嚴格遵循幾何規律，在畫的過程中進一步理清問題給出的條件，延伸出由直接條件得出的簡單結論，能給問題找出更多有用的條件。

在平常的練習中可以用"幾何畫闆"來畫圖，幾何畫闆作圖快捷，作出的圖形始終保持幾何屬性，無論怎樣驚變形狀，作出的垂直始終保持垂直狀态，有助于分析動态問題。

• 2. 在圖形上标注好等量

畫完圖後，開始分析問題，在圖中把已知條件中給出的相等關系的量（相等的線段、相等的角）或能夠知道相等的關系的量用相同的符号進行标記。

并把條件中已知的線段長度、角的度數或者通過簡單分析能得出的長度、角度做上标記。題中有多組等量，要用不同的标記，以免混淆。比如相等的線段可在線段上劃小斜線，相等的角用小弧線。複雜的角用阿拉伯數字标注，如∠1，∠2等等。

作标記有兩個好處，一是有利于我們分析圖形，二是能夠使書寫的證明過程簡潔、明了，可讀性增強，在證明過程中遇到的角也可以用數字标記出來便于書寫和閱讀。

• 3. 找出圖中隐含的基本圖或模型圖

原圖中通過延長線段、連結兩點、作垂直、作平行等輔助線後得到的特殊圖形，如平行、垂直、特殊三角形（等邊三角形、等腰三角形、Rt三角形）、特殊四邊形（正方形、矩形、菱形、平行四邊形、等腰梯形等），這些特殊圖形能夠為我們提供諸如"相等"、"平行"、"垂直"等關系。

數學學習過程中有許多基本的幾何模型，往往在難題中能找到這些基本模型的影子，如"三線八角"模型、"旋轉全等模型"、"半角模型"等，基本幾何模型有特有的性質特點，能夠發現這些模型，就能找到更多條件。

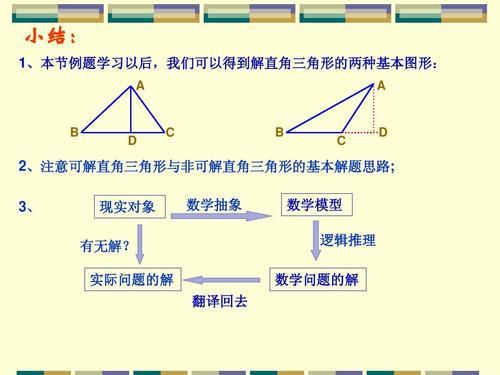
數學模型

• 4. 善用數形結合

數形結合法是解決數學問題的重要方法之一，體現了數量關系與空間形式是相互聯系和轉化的，将抽象的數式與具體的圖形相結合與轉化，把圖形問題轉化為數量關系進行研究，以數解形，先充分挖掘出圖形中的數量關系，用代數式求解幾何問題，根據圖形建立方程或函數關系是常用的方法。

比如在解決一些幾何題時，可嘗試将圖形放入數軸或者是平面直角坐标系中，把幾何問題代數化，再如要證明三角形是直角三角形時，可嘗試将三邊長度用勾股定理來驗證。

#樹人新力量##五一小長假##頭條教育#

更多精彩资讯请关注tft每日頭條，我们将持续为您更新最新资讯!