楊輝，字謙光，漢族，錢塘(今杭州)人，南宋傑出的數學家和數學教育家，生平履曆不詳.由現存文獻可推知，楊輝擔任過南宋地方行政官員，為政清廉，足迹遍及蘇杭一帶，他署名的數學書共五種二十一卷.所著的《詳解九章算術》（1261年)一書中用如圖的三角形解釋二項和的乘方規律.

楊輝三角，是二項式系數在三角形中的一種幾何排列。在歐洲，這個表叫做帕斯卡三角形。帕斯卡（1623----1662）是在1654年發現這一規律的，比楊輝要遲393年，比賈憲遲600年。楊輝三角是中國古代數學的傑出研究成果之一，它把二項式系數圖形化，把組合數内在的一些代數性質直觀地從圖形中體現出來，是一種離散型的數與形的優美結合.

仔細觀察楊輝三角的圖形，你能發現組成它的數有什麼排列規律嗎？

它的前幾層是這樣的：楊輝三角的兩條斜邊都是由數字1組成的，而其餘的數則是等于它肩上的兩個數之和，以此類推。動态數字展示如下：

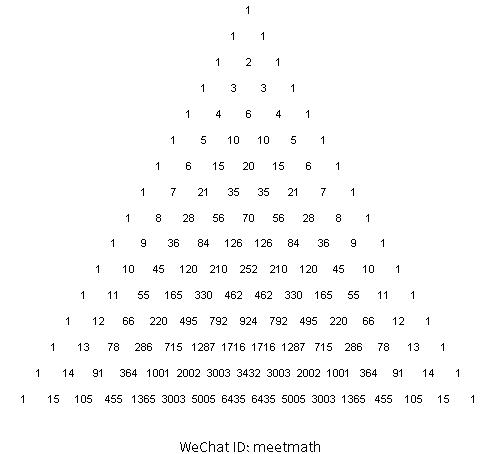
楊輝三角多彩的性質展示如下：

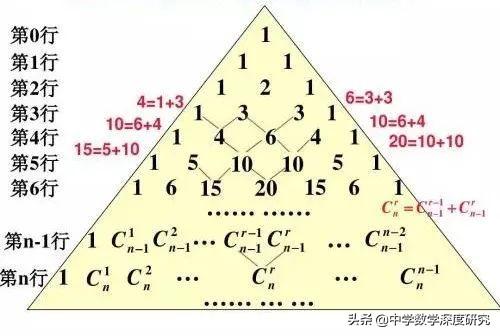
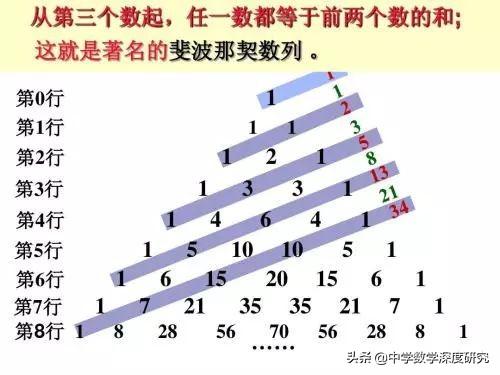
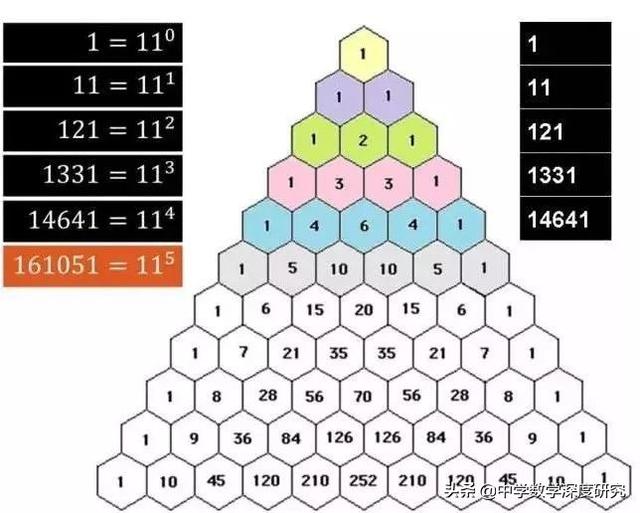
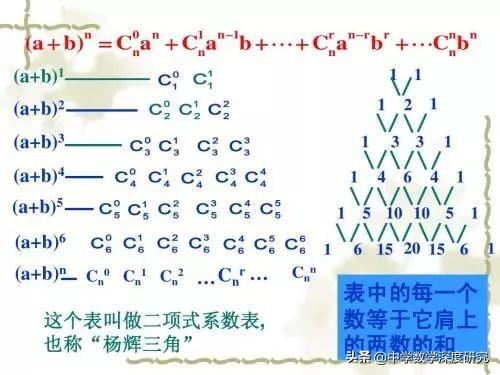
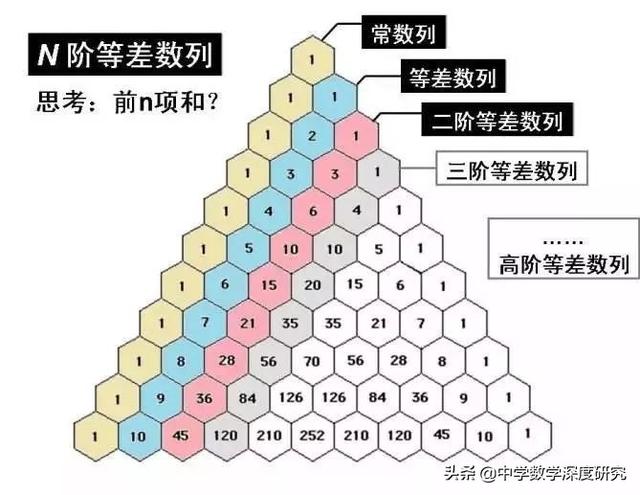
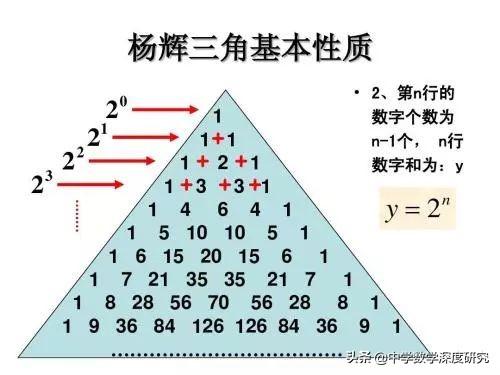
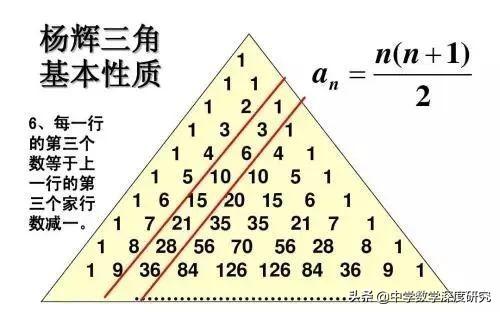
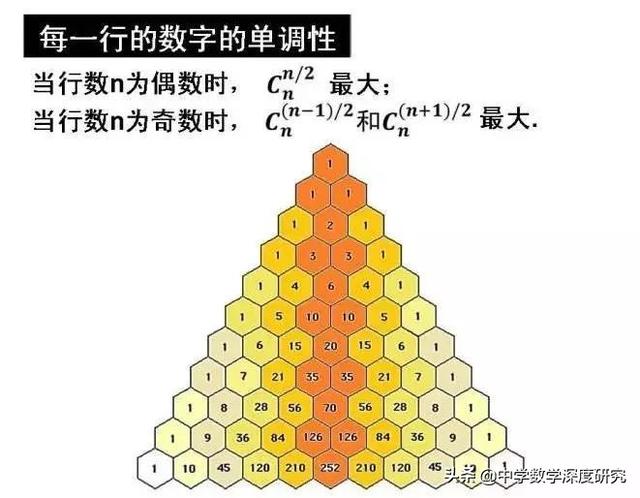
楊輝三角是我國古代數學的瑰寶，它不僅像上面呈現了二項式定理中有關二項式系數的性質與規律，而且其本身還包含着許多有趣的規律、結論與性質．正因為如此，以楊輝三角為背景的試題在近年的各地中高考或模拟卷中時有出現，下面就讓我們來看看其中一些常見的問題．

例1.如圖是與楊輝三角有類似性質的﹣三角形數壘，a、b、c、d是相鄰兩行的前四個數（如圖所示），那麼當a＝8時，c＝____ ，d＝______．

【解析】觀察發現：第n行的第一個數和行數相等，第二個數是1 1 2 … n﹣1＝n(n-1)/2 1．所以當a＝8時，則c＝9，d＝9×4 1＝37．

例2.如圖為與楊輝三角結構相似的"巴斯卡"三角，這個三角的構造方法是：除第一行為1外，其餘各行中的每一個數，都等于它右肩上的數乘以右肩所在的行數，再加上左肩而得．例如第5行第3個數是35，它的右肩為6，左肩為11，右肩所在的行數為4，所以35＝6×4 11．這個三角中的數與下面這個展開式中的系數有關：

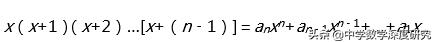
則在"巴斯卡"三角中，第8行從左到右的第2個數到第7個數之和為（ ）

A．322559 B．35279 C．5880 D．322560

【解答】由已知中"巴斯卡"三角的前5行可得：第n行的第一個數為（n﹣1）!，故第8行的第一個數為：7!，第9行的第一個數為：8!，又由：第一行的累加積等于第二行的第一個數；第二行的累加積等于第三行的第一個數；第三行的累加積等于第四行的第一個數；第四行的累加積等于第五行的第一個數；…，故第8行的所有數的和為：第9行的第一個數8!，設第8行從左到右的第2個數到第7個數之和為S，則S 7! 1＝8!，故S＝8!﹣7!﹣1＝35279故選：B．

本題結合楊輝三角數表中的數值的排列規律，在"新問題""新背景"下，再次尋找"新規律" "新思路"，以此，在學習與再探究過程中，培養學生體驗數學方法，實現對"新問題""新思路"的探究．

很多讀者迷迷糊糊，疑惑楊輝三角存在的現實意義是什麼呢？簡單地說楊輝三角如縱橫路線圖問題：

又如彈球遊戲多問題：觀察下圖，小球落在AG兩區域的概率要比其他區域小得多，當然得到的遊戲獎品就更多一些。從該圖中不難發現，各區域的概率與楊輝三角形有密切聯系，我們可以直接利用楊輝三角的性質得出小球落到每個區域的概率。

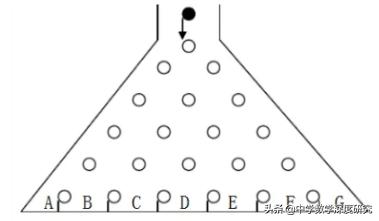
簡單化處理，我們求解這樣問題：如圖所示是在豎直平面内的一個"通道遊戲"．圖中豎直線段和斜線段都表示通道，并且在交點處相遇，若豎直線段有一條的為第一層，有二條的為第二層，依此類推，現有一顆小彈子從第一層的通道裡向下運動．并且小彈子落入每一條通道的可能性相同，則該小彈子從第三層通道的出口B脫出的概率為 ______．

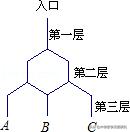
【解答】第2層的2個出口都有可能從B通過，∴小彈子從第三層通道的出口B脫出的概率為2/(1 2 1)=1/2，

"堆垛術"也與楊輝三角有關系。将許多球堆成三角垛：底層是每邊 個球的三角形，向上逐層每邊少一個球，頂層是一個球，求總數。

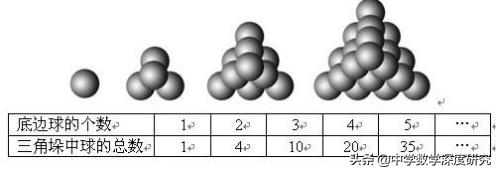
底邊球的個數 1 2 3 4 5 …；三角垛中球的總數 1 4 10 20 35 …；這時自然發現了三角垛中球的總數正好是楊輝三角中第4個斜向數組！

楊輝三角就像一座數學寶庫，其間應有盡有!古老的楊輝三角的某些優美的性質在現代生活中得到了充分的體現，令人不由為燦爛的古代文明新生自豪之情。楊輝三角，不隻是一片雲彩，它是熠熠生輝的中國古代數學瑰寶！

更多精彩资讯请关注tft每日頭條，我们将持续为您更新最新资讯!